GPS定位系统中几种对流层模型的探讨

赵铁成,韩曜旭

(中国人民解放军61769部队,黑龙江 哈尔滨150039)

0 引 言

所谓对流层即为从地面向上约40 km范围内的大气层,整个大气层质量的99%几乎都集中在该层中。对流层与地面接触,具有很强的对流作用。风、雨、云、雾、雪等主要天气现象,均出现在该层中,该大气的成分除含有各种气体元素外,还含有水滴、冰晶、尘埃等杂质,它们对电磁波的传播产生很大影响。由于对流层中空气的折射率在不断变化,因此,当GPS信号通过对流层时,在传播的路径上会产生弯曲和延迟两种效应,因此使测量距离产生误差。对流层延迟的影响还与信号的高度角有关,对于一个海平面上的中纬度站,在天顶方向(高度角为90°)其影响达2 m;在地面方向(高度角为10°)其影响可达20 m[1-2]。

1 对流层路径延迟

电磁波在对流层中传播与在真空中传播相比,会导致额外的路径长度,即弯曲和延迟。其额外的路径长度可表示为

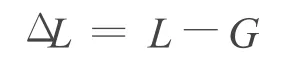
式中:L=∫n(s)ds,即电磁波走过的实际路径长度;L为沿着曲线路径;G为卫星与GPS接收机之间的直线长度。这部分额外的路径几何长度(LG)仅占全部路径延迟的0.1%左右,常忽略不计。因此,对流层中的路径延迟主要归因于信号的阻滞,这部分表示为

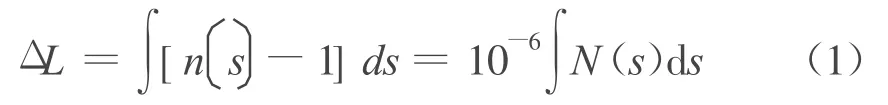
式中:N=(n-1)×106为大气的折射率;n为传播路径上空气的折射指数。在假定折射率是关于球面对称的前提下,上式中的s可用r代替(r是地球中心至传播路径上任意点的半径)。空气的折射率常用经验公式表述,且与空气的热力学状态变量有关。大气折射率是空气密度ρ(kg/m3)和水汽密度 ρv的函数:

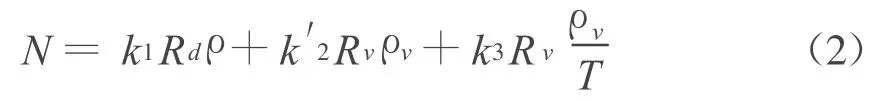
式中:k1是折射率常数;而k′2=k2-(Rd/Rv)k1;Rd和Rv分别是干燥空气和水汽常数;T是大气的绝对温度(单位K)。使用映射函数法可避免烦琐的三维大气折射率,其主要假设是在任意方向上的路径延迟均与天顶方向路径延迟相关。因此方程式(1)可重写为

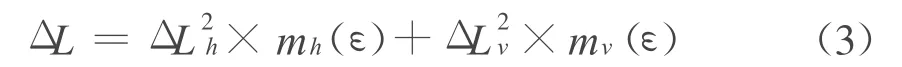
式中:mh(ε)和mv(ε)分别是静力学和湿映射函数;ε是地面测站的仰角;和分别是天顶静水力学和湿延迟分量。由下式给出

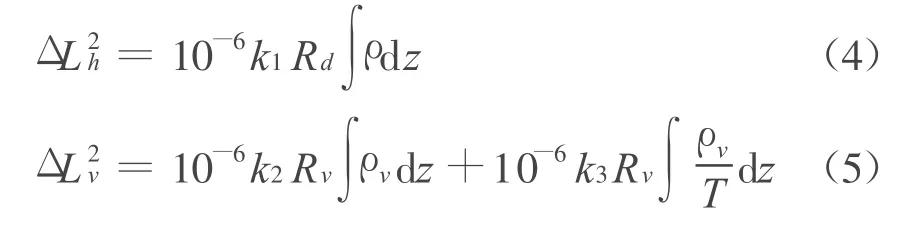
2 对流层延迟改正

目前,常用的对流层延迟修正模型计算方法分为直接计算法和利用映射函数计算等。直接计算法主要有霍普菲尔德(Hopfield)模型、萨斯塔莫宁(Saastamoinen)模型、勃兰克(Black)模型、WAAS系统对流层修正模型和EGNOS系统对流层修正模型;利用映射函数计算方法主要有CFA模型、Chao模型 、Mit模型、Marini&Murray模型、Niell模型和GMF模型等。

2.1 直接计算法

2.1.1 霍普菲尔德(Hopfield)模型

霍普菲尔德(Hopfield)模型[3-6]是一种较为普遍的大气折射延迟模型,它简单地将大气层分为对流层和电离层,其天顶总大气延迟为

式中:HT、HW、P0、T0、e0和h分别为干大气层顶高、湿大气层顶高、地面气压(mbar)、地面温度(T)、地面水气压(mbar)和测站在大地水准面上的高度(m);常参数K1=77.6 K/mbar、K2=71.6 K2/mbar、K3=3.747×105K2/mbar.

霍普菲尔德(Hopfield)模型可以计算斜延迟的校正公式为

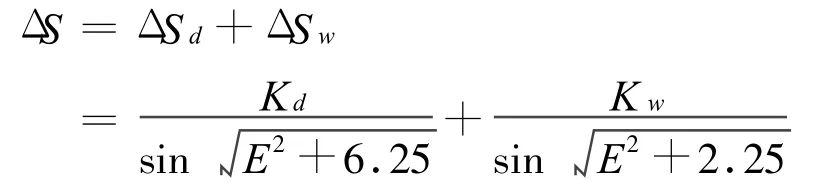
式中:

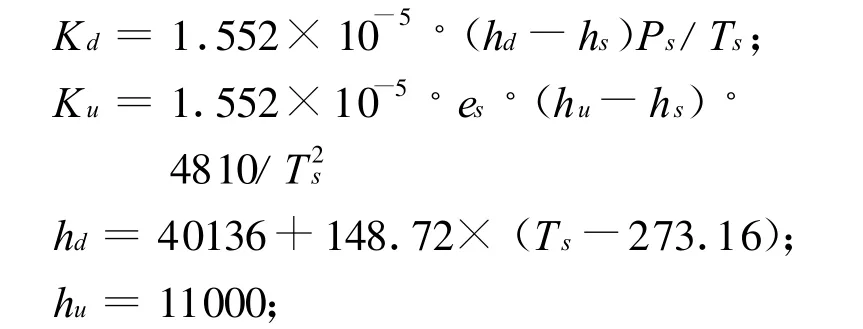
式中的温度均采用绝对温度,单位为K;P、es的单位为mbar;Δ S、hd、hs以m为单位;仰角E以角度为单位。通常水汽压es可以用湿度RH来计算,关系式为

2.1.2 萨斯塔莫宁(Saastamoinen)模型

萨斯塔莫宁模型[6-9]把地球的大气分为3层:对流层是从地面到10 km左右高度处的对流层顶,其气体温度假设为6.5℃/km递减率;第二层是对流层顶到70 km左右的平流层顶,其中把大气温度假设为常数;70 km以外是电离层,大气折射改正的基本数学表达式为

在对上式积分时,Saastamoinen模型主要贡献是首次把被积函数按照天顶距三角函数进行展开逐次进行积分,得到大气天顶延迟改正为

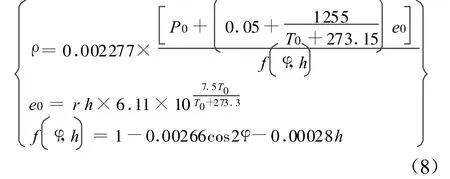
其中,P0、T0、e0、rh、f(φ,h)、φ和h分别为地面气压(mbar)、地面温度(°C)、地面水气压(mbar)、相对湿度(0～1)、地球自转所引起重力加速度变化的修正、台站的地心纬度(°)和测站大地高(km)。

萨斯塔莫宁(Saastamoinen)模型可以计算斜延迟的校正公式为

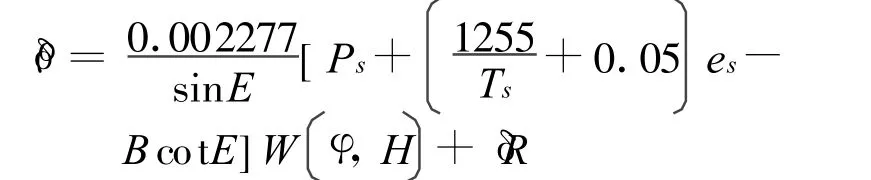
由于在实际应用中,上式不便于实时快速计算,在保证其适用精度的前提下,对上式进行拟合化简,拟合化简后的萨斯塔莫宁(Saastamoinen)模型为

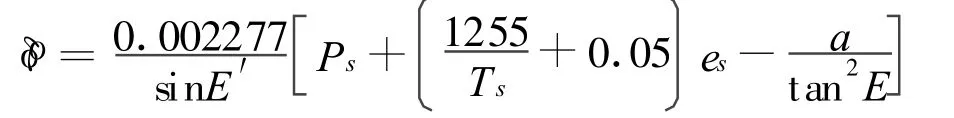
式中:

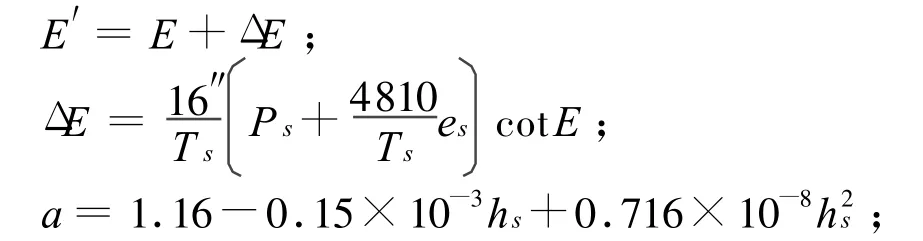
E为仰角(°);Ps是测站气压mbar;Ts是测站气温(绝对温度);es是测站水气压mbar。

当没有实测气象数据时,利用 Hopfield和Saastamoinen模型计算对流层天顶延迟所需的气象参数可以利用加拿大新布朗斯威克大学开发的DIPOP软件中的设置[10]得到。

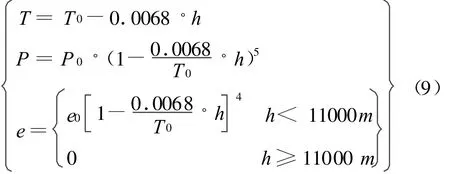
标准参考大气参数,P0=1013.25 mbar,e0=11.691 mbar,T0=288.15K,h为海拔高(m)。

2.1.3 勃兰克(Black)模型

霍普菲尔德(Hopfield)模型没有考虑信号传播的路径弯曲,H.D.Black于1978年,在霍普菲尔德(Hopfield)模型的基础上加入路径弯曲之后,给出了勃兰克(Black)模型的表达式

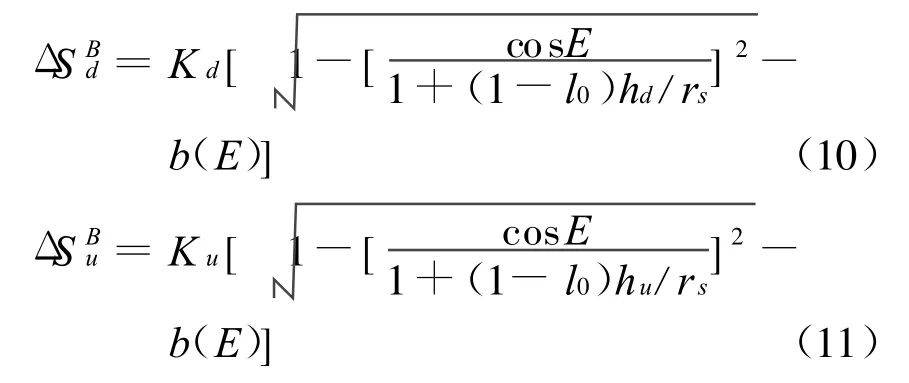
式中:

其中,rs=R0+hs;R0为地球半径;l0和路径弯曲改正因子b(E)由下式确定:

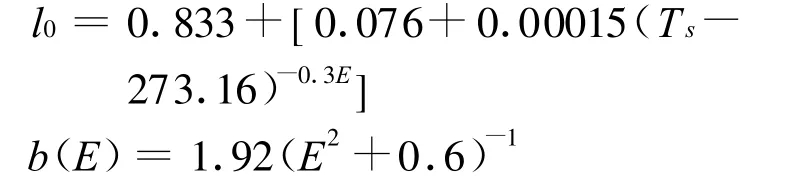
式中的温度均采用绝对温度,单位为K;P、es的单位为mbar;Δ S、hd、hs以m为单位;仰角E以度(°)为单位。

2.1.4 WAAS系统对流层修正模型

对流层延迟随温度、压力和相对湿度而变。对于对流层延迟,接收WAAS信号的接收机采用测定随季节变化的平均信号延迟(对于仰角大于5度(°)的卫星有效),计算如下

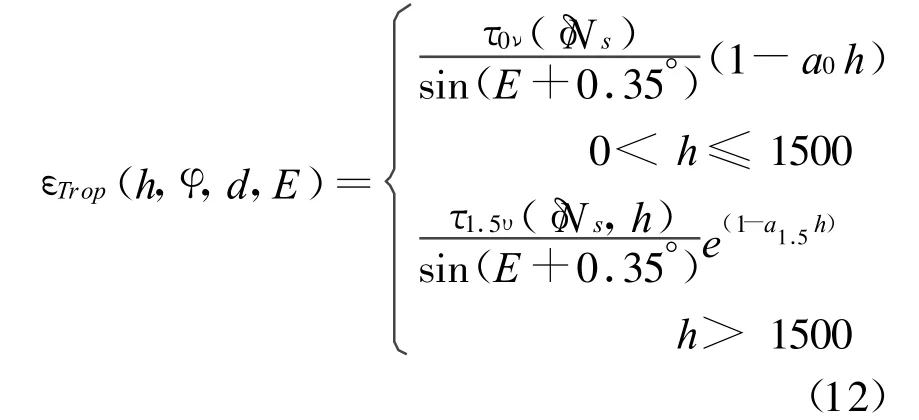
式中:h是用户的海拔高度(单位m);φ是用户所处的纬度(单位°);d是一年内的天数。其它参数如下:

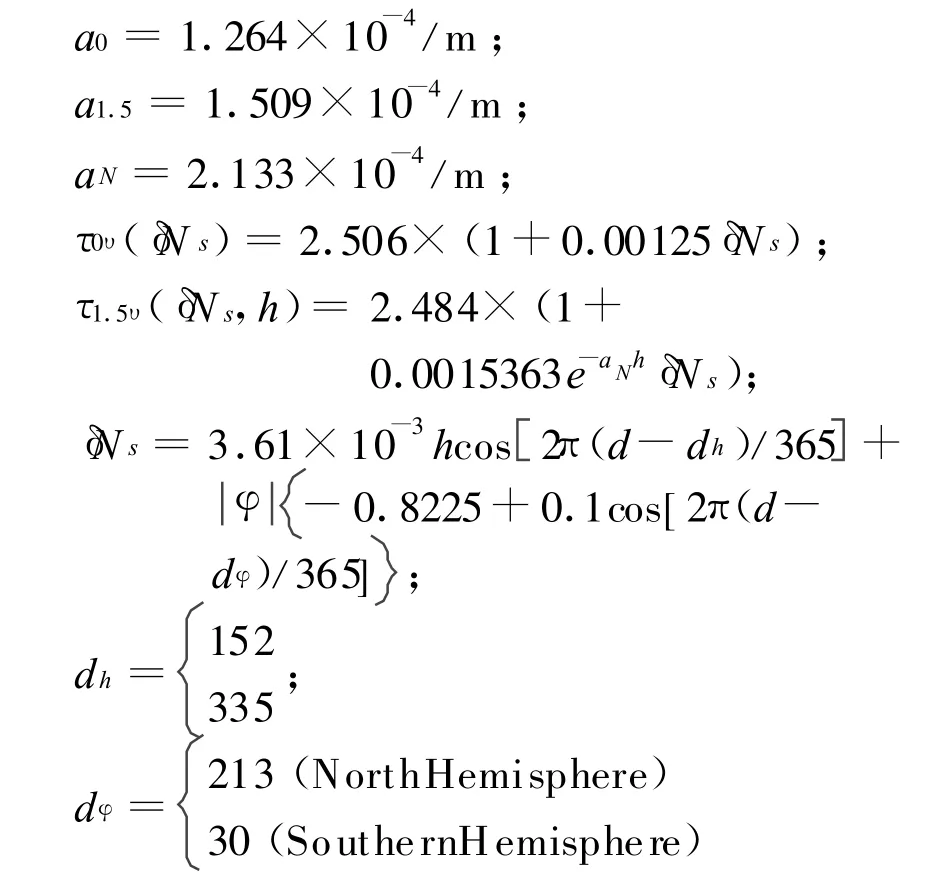
WAAS对流层模型是用温度、压力和相对湿度测量值所获得的精度和用地球折射率全球平均值所获得的精度之间的折衷产物。根据地球表面的全球平均折射率估计的延迟会产生误差,误差的标准偏差大约是真实延迟的8%。如果把用户的纬度、海拔高度、季节和仰角都考虑进去,对于对流层延迟估计值改善25%来说,这个标准偏差可降到6%。

2.1.5 EGNOS系统对流层修正模型

EGNOS模型是欧盟的EGNOS(the European Geo-stationary Navigation Overly System)所采用的对流层天顶延迟改正模型。EGNOS系统用经典的经验公式来计算对流层延迟,其最大好处是计算天顶延迟时,不需要实测的气象数据。该模型提供计算对流层天顶延迟所需的5个气象参数(气压、温度、水蒸汽压、温度下降率、水蒸汽下降率),它们在平均海平面上的时空变化仅与纬度和年积日有关,且其年变化呈余弦函数,每个参数余弦函数的相位固定(最小值的年积日北半球取为28日,南半球为211日),余弦函数的振幅和年平均值由气象资料拟合求得。

接收机的对流层天顶延迟的计算是:先由接收机的纬度和观测日期求得平均海平面的5个气象参数,则可计算相应的平均海平面的天顶延迟,然后由接收机的高程计算接收机处的对流层天顶延迟.EGNOS模型能较好地描述平均对流层延迟,其数学模型如下:

由平均海平面的天顶延迟计算接收机处的天顶延迟:

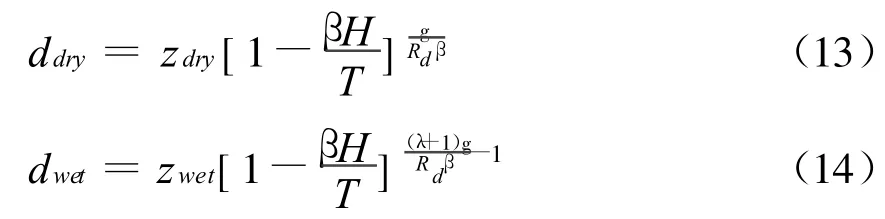
式中:ddry是天顶的“干”空气延迟;dwet是天顶“湿”空气延迟;Zdry是平均海平面的“干”空气延迟;Zwet是平均海平面的“湿”空气延迟;H是接收机对海平面的高度(m);T是平均海平面的温度(K);β是温度下降率(K/m);λ是水蒸汽湿度下降率;g=9.80665 m/s2;Rd=287.054 J/Kg/K。

平均海平面的“干”空气延迟:

平均海平面的“湿”空气延迟:

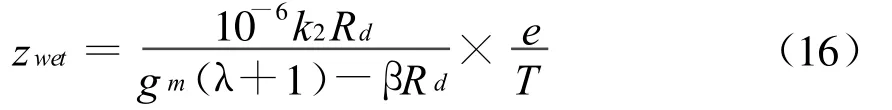
式中:k1=77.604 K/mbar;k2=382000 K2/mbar;gm=9.784 m/s2;P是平均海平面气压(mbar);e是平均海平面水气压(mbar)。

平均海平面的气象参数P、T、e、β、λ的计算公式:

其中:ξ(φ,D)为5个气象参数,它仅与接收机的纬度 φ和观测的日期D(年积日)有关;ξ0(φ)为各气象参数的年平均值;Δ ξ(φ)为各气象参数的季节变化值;Dmin为各气象参数的年变化的最小值的日期(北半球Dmin=28,南半球Dmin=211)。

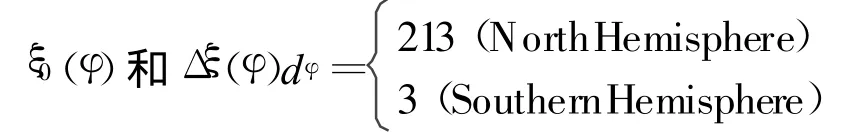
可由在纬度范围(φ+Δ φ,φ-Δ φ)内的全球(或某区域)平均海平面的各气象参数拟合求得.表1和表2分别列出了不同纬圈5个气象参数的年平均值和季节变化值。

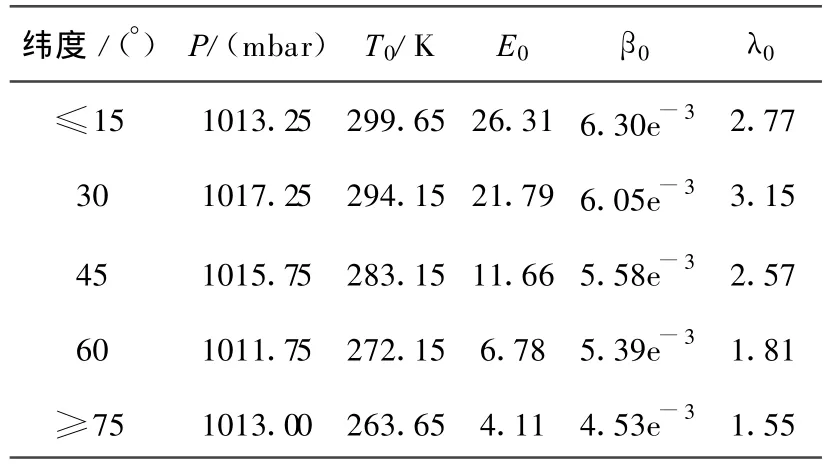
表1 平均值

表2 季节性变化

2.2 利用映射函数计算对流层延迟

电磁波在对流层传播速度延迟的计算方法一般可用天顶延迟值与卫星高度角的投影函数两部分的乘积求得,即:

天顶延迟值的确定一般采用Saastamoinen模型结合随机过程参数估计的方法,精度较高;而投影函数是一种经验模型,其精度取决于母模型的精度和实地观测资料的情况。以下详细列举了CFA模型、Chao模型、Mtt模型、Marini&Murray模型、Niell模型、和GMF模型的投影函数公式,用以计算对流层延迟。

由大气物理的有关知识,大气折射率N分为干分量和湿分量两部分。即对流层延迟由干气延迟和湿气延迟两部分组成。干气延迟占总延迟的80%～90%,比较有规律,在天顶方向约1%的精度估计;但湿气延迟比较复杂,影响因素也比较多,目前只能以10%～20%的精度估计。式(18)可以改写成用天顶方向的干、湿延迟分量及相应的映射函数来表示:

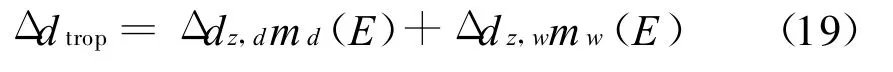
式中:Δ dz,d、Δ dz,w分别为天顶方向的干、湿延迟分量;md(E)、mw(E)分别为与高度角E有关的映射函数。

采用Saastamoinen模型的天顶干湿延迟为

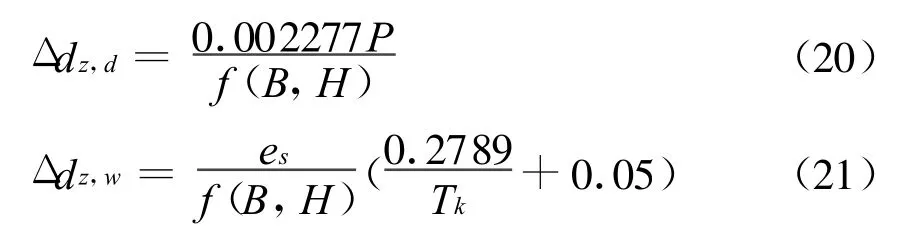
式中,P、es、Tk分别为测站的大气压(mbar)、水气压(mbar)、绝对温度(K)。

f(B,H)为测站纬度B和高程H的函数,f(B,H)=1-0.00266cos2B-0.00028H

这样,选择合适的函数后,由式(19)、(20)、(21)式即可求得传播路径上的对流层折射改正数。

2.2.1 CFA2.2映射函数模型

CFA2.2映射函数式Davis等人于1985年在Marin连续性映射函数的基础上改进得来的,它一直广泛应用于VLBI和GPS等空间技术中。该模型中的系数式从双层射线跟踪分析得出的,当高度角大于5°时,模型具有5 mm的精度[18]。

CFA2.2模型[14]的干湿分量映射函数相同,为

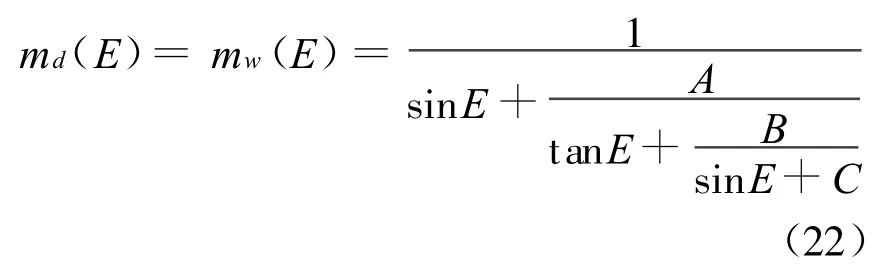
式中:

2.2.2 Chao映射函数模型

Chao给出了一个二次连分投影函数,其经验系数取自无线电探空资料所计算的射线结果,曾一度被广泛采用。其映射函数形式为

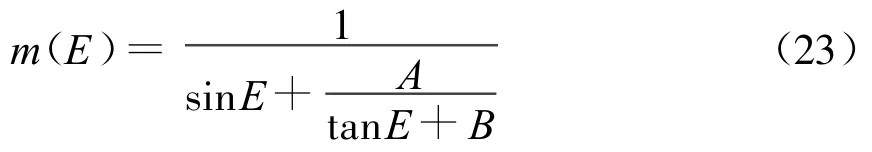
对于干分量的映射函数,式(23)中的常数A=0.001433,B=0.0445;对于湿分量,式(23)中的常数A=0.00035,B=0.017.

2.2.3 Mtt模型映射函数

Mtt模型[17]的映射函数形式为

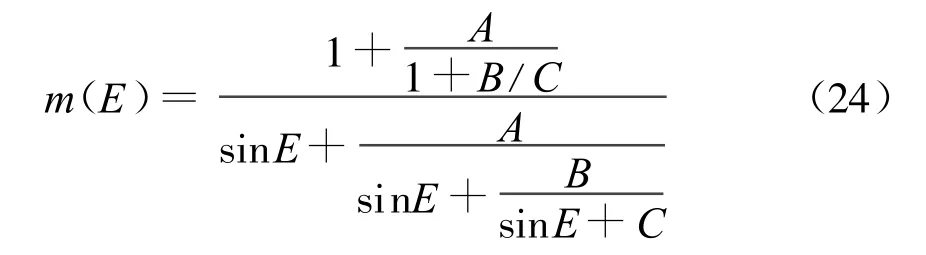
对于干分量的映射函数,式(24)中:

对于湿分量的映射函数,式(24)中,

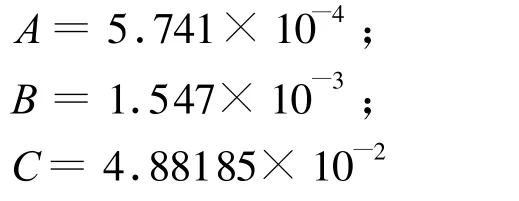
2.2.4 Marini&Murray模型的映射函数

Marini&Murray模型[15-16]是常参数连分式映射函数中,使用等温假设下的指数大气模型。其映射函数干湿分量映射函数相同,为

式中:

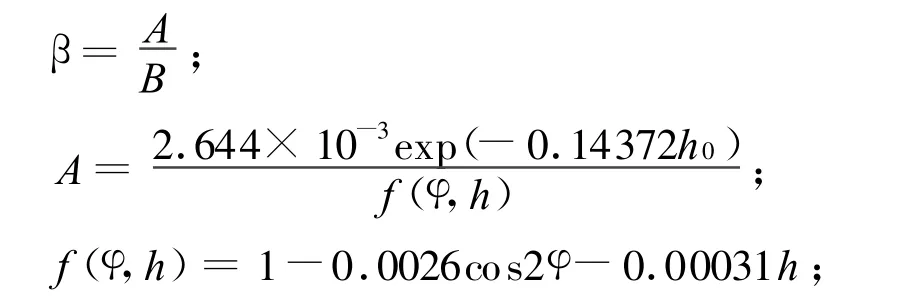
B为Saastamoinen的总延迟值公式,如式(8)所示。

2.2.5 NMF模型映射函数

Niell应用了26个全球分布的探空气球资料,建立了在无线电波长上的一个“全球大气延迟投影函数”,称为 NMF模型[12]。相比于其他模型,NMF加入了一个投影函数改正量Δ MF(el),且其中的系数a,b,c表示为与测站地面气象记录完全不相关的测站地理纬度φ、地理高度和年积日(d)的函数。

模型干分量

式中:

令x=a,b,c,则式(27)中相关系数可表示为

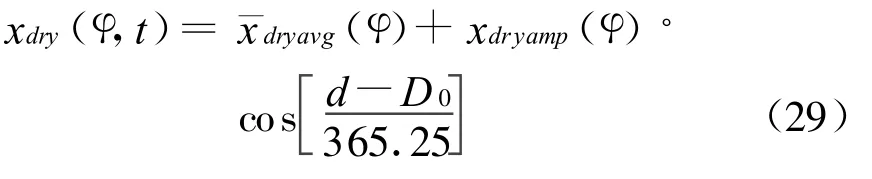
另外,

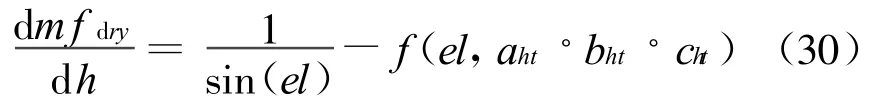
模型湿分量

其中,式(27)中的干项系数adry、bdry、cdry,式(29)中 的 系 数 均值 ¯xdryavg(φ)、系 数速率式(30)中的高度改正,以及式(31)中的aht、bht、cht3个湿项系数均可由按纬度查询的表中得到,详表可参见文献[6]。

2.2.6 GMF模型映射函数

NMF模型是建立在北半球分布的一年中的电波资料基础上的,该模型的空间和时间变量只受纬度和季节影响。由于没有其他客观的数据,该经验模型的模拟过程显得过于简单化。而GMF模型是采用数值天气模型(NWM)提供的高精度全球对流层折射率来解算延迟量,其参数是建立在15°×15°全球格网及WCMWF(欧洲中期天气预报中心)提供的40年气压、温度和湿度分析数据基础上的[13],并且考虑到测站经度对解算的影响,但模型较为复杂。

干分量

式中:

其中,当测站处于北半球,即φ≥0,则phh=0;ch1=0.007;ch0=0.002;当测站处于南半球,即 φ≤0,则phh=π;ch1=0.005;ch0=0.01

式中:aht=2.53×10-5;bht=5.49×10-3;cht=1.14×10-3。

湿分量

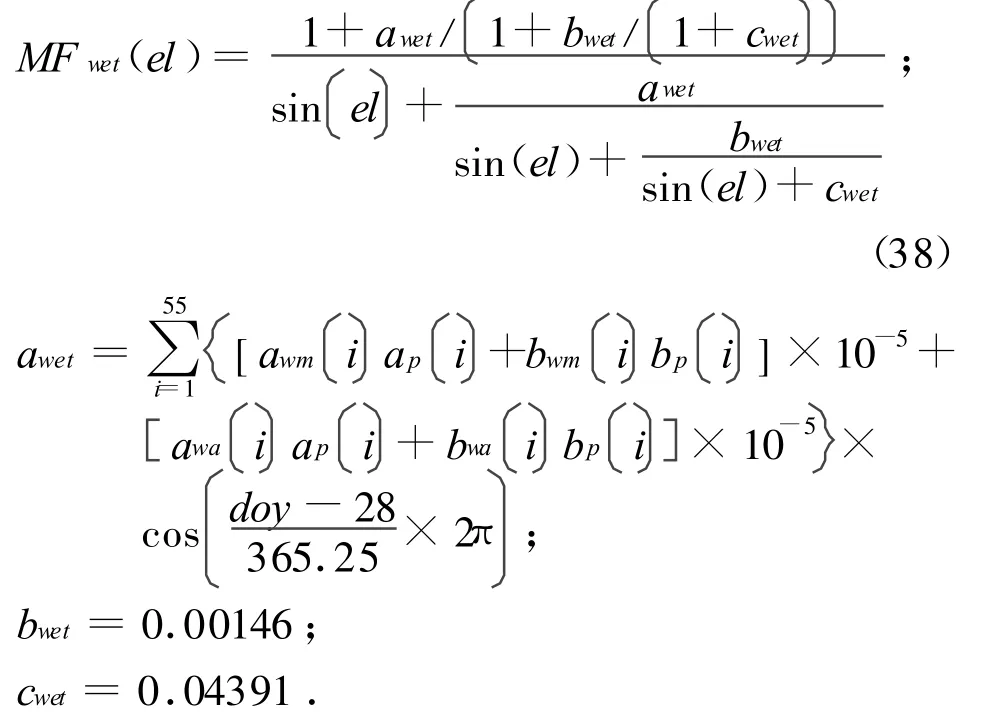
其中,系数ahm、bhm、aha、bha、awm、bwm、awa和bwa均可查表确定。

3 结 论

对流层延迟误差在GPS的精确定位中不容忽视,本文对对流层模型进行比较全面的介绍,对计算模型方法进行分类并给出相应模型公式,对模型应用也给出了必要的说明。其实,估算对流层误差最有效的方法是先在每点上估算对流层延时,然后按每时段去求平均值。具体应用以上误差模型还要根据实际情况和数据的处理情况决定。对流层的时延误差主要影响高程精度,两点之间高差越大,对流层误差越大。目前,对流层延迟的研究进展主要有反映水平不均匀的映射函数和基于数值天气预报的映射函数等,其对流层误差依然是提高GPS测量高程分量精度的主要障碍,研制出更精确的对流层模型是今后GPS科技工作者的一项重要任务。

[1] Brunner F K,Welsch W M.Effect of the troposphere on GPS measurements[J].GPS World,1993,4(1):42-51.

[2] Van Der Marel H.Virtual GPS reference stations in the netherlands[C]//ProceedingsION GPS-98,Nashville,1998:49-58.

[3] Hopfield H S.Applied Phys.lab report CPO 15[R].Baltimore,Maryland:JohnsHopkinsUniversity,1972.

[4] Hopfield H S.Two-quadratic tropospheric refractivity profile for correcting satellite data[J].Journal of Geophysical Research,1969,74(18):4487-4499.

[5] Hopfield H S.Tropospheric effect on electromagtically measured range:prediction from surface weather data[J].Rad Sci.,1971(6):357-367.

[6] 杨 力.大气对GPS测量影响的理论与研究[D].中国人民解放军信息工程大学,2001.

[7] Saastamoinen J.Contributions to theory of atmospheric refraction[J].Journal of Geodesy,1972,105(1):279-298.

[8] Saastamoinen J.Introduction to practical computation of astronomical refraction[J].Journal of Geodesy,1972,106(1):383-397.

[9] Saastamoinen J.Contributions to the theory of atmospheric refraction Part II.Refraction corrections in satellite geodesy[J].Journal of Geodesy,1973,107(10):13-34.

[10] 陈小明,刘基余.GPS动态定位的对流层改正模型.[J].导航,1996,32(2):44-46.

[11] Janes H W,langley R B,Newby S P.Analysis of tropospheric delay prediction models:comparisons with ray-tracing and implications for GPS relative positioning[J].Journal of Geodesy,1991(65):151-161.

[12] Niell A E.Global mapping functions for the amosphere delay at radiowavelengths[J].Journal of Geophysical Research,1996,101(B2):3227-3246.

[13] Boehm J,Niell A.Globalm apping function(GMF):A new empiricalm apping function based on num erical weather model data[J].Geophysical Research Letters,2006(33):1-4.

[14] Davis J L,Herring T A,Shapiro I I,et al.Effect of at atmospheric modeling errors on estimates of baseline length[J].Radio Science,1985(20):1593-1607.

[15] Marini J W.Correction of satellite tracting data for an arbitrary tropospheric profile[J].Radio Science,1972(7):223-231.

[16] Marini J W.Correction of satellite tracking data for an arbitrary tropospheric profile[J].Radio Science,1971,7(2):223-231.

[17] Herring T A.M odeling atmospheric delays in the analysis of space geodetic data[C]//Proceedings of Refraction of Transatmospheric Signals in Geodesy,Netherlands Geodetic Commission Series, The Hague,Netherlands,1992(36):157-164.

[18] Elgered G.Troposphericradio path delay from groundbased microwave radiometry[M]∥ Janssen M A.Atmospheric remotesending by microw are radiom etry,Wiley&Sons,1993:215-258.