多目标缓冲区生成算法
白 帆,张福浩
(1.兰州交通大学,甘肃 兰州730070 2.中国测绘科学研究院,北京100083)
0 引 言
缓冲区分析是地理信息系统重要和基本的空间操作功能之一[1]。其实现的功能就是在给定的地理实体集合周围建立起一定距离的多边形,以代表该地理实体集合对周围物体环境的影响范围及程度。缓冲区分析是GIS空间分析中基本的功能之一,是很多空间分析方法的基础。空间分析是基于地理实体的位置和形态特征而获取新的空间信息的数据分析方法。缓冲区分析广泛应用在地理信息系统的各种分析中,例如在水污染监测、城市规划与管理、地震灾害和损失估计、洪水灾害分析、矿产资源评估、道路交通管理、地形地貌分析等领域都有广泛应用[2-3],如评估城市中道路的噪声对附近的某居民区有无影响、海上漏油点对附近海域环境污染范围;计算一个国家领海的范围等。
1 缓冲区生成基本算法
缓冲区的生成算法有栅格和矢量两种基本方法。栅格方法又叫点阵法。其基本原理是将矢量图形栅格化,对要进行分析的地理实体进行像元加粗,然后提取其边缘。该方法在原理上比较简单,实现也容易,但是其精度受限,而且在面对大数据量的分析时内存开销大,受性能影响较大。矢量方法原理较栅格方法复杂,但其精度高,是本文讨论的对象。
矢量方式的缓冲区生成包括点、线和面三种目标缓冲区的生成。点的缓冲区生成是以该点为圆心,给定距离为半径的圆。通常是以正 n边形表示,缓冲区的精度取决于n的大小。线缓冲区生成算法常用的方法是角平分线法和凸角圆弧法。角平分线法的缺点是难以最大限度的保证平行曲线的等宽性,矫正过程复杂,不易完备的实现[4]。为了避免上述缺点,本文采用凸角圆弧算法。面缓冲区的生成是对面的外边界线的内外做平行线,实现方法同线缓冲区生成大致相同。其中线状目标的缓冲生成是缓冲区算法中的核心。
2 改进后的缓冲区算法
该算法是由缓冲半径绕点旋转生成目标缓冲区边界并将生成的缓冲区进行合并的一种可靠、简便的方法,简化了多目标缓冲区生成的过程。下面就点和线的生成过程及在缓冲区生成过程中出现的特殊情况进行讨论。
地理信息系统中的曲面通常是以有序点的方式表示,如圆形一般是以正n边形来近似表示的。因此只要得到了构建缓冲区曲线的有方向性有序点集,即可以得到缓冲区的曲面。
2.1 点缓冲区生成算法
点缓冲区是缓冲区生成中比较简单的一种,即用正n边形的相应折线段来近似表示点状的缓冲区。其中正n边形的边数可以代表点缓冲区的“平滑度”,即缓冲区多边形中曲线的分辨率。如果该值取的太小,放大后曲面的锯齿较为明显;如果取得较大,则运算量增大影响运算速度。通常在实现中取16及以上较为适宜,如图1所示。
在平面上任一点(X,Y)关于任意点(Xr,Yr)旋转θ角,得到新点的位置坐标(X′,Y′)的公式

此时X-Xr=r,Y-Yr=0,上面公式则变为
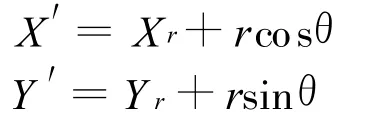
如图1所示,作点目标O的缓冲区边界多边形。以缓冲区半径作为AO的长度,根据上述公式取旋转角θ=0,δ,2δ,3δ…,n*δ,此时的步长 δ由正n边形的边数决定,即 δ=2π/n。从而就可以得到用来表示点缓冲区的正n边形的各点坐标。其中需要注意在最后应将首点加入到坐标点序列中,以使多边形闭合。

图1 点缓冲区生成
2.2 线缓冲区生成算法
线状目标缓冲区生成可以分为双侧缓冲区和单侧缓冲区,以及双侧不对称缓冲区。这里以使用最多的双侧缓冲区为例说明,其他类型与之类似。
线状目标是矢量,具有方向性。在生成线状目标缓冲区时先做第一个点的右侧缓冲区,然后按照线状目标的走向依次做相邻两点及最后一点的右侧缓冲区线段,然后将点顺序倒置,重复上述过程。所有目标缓冲区生成以后,依次判断各缓冲区有无相交。如果有相交则做相交处理;如果没有相交则将其从缓冲区队列中删除并加入到最后的结果队列中。
下面以一个例子来具体说明该算法生成线状目标缓冲区的实现过程。
1)沿线状目标前进方向,先做首端点的左侧缓冲区;
与上述的点缓冲区生成方法相似,使用正n边形来近似替代圆弧。应该注意圆弧段的起始角度和终止角度。连接首端点和第二个结点,形成向量AB。向量AB沿顺时针方向旋转到X轴正半轴扫过的角度为θ。起始角度是θ+π,终止角度是θ+3π/2,其中每次增加角度2π/n。图2中对应首端点生成了线缓冲区边界多边形上 A段上的若干点。

图2 线缓冲区生成
2)作线状目标首端点和末端点之间点的右侧缓冲区。
假设现在进行判断的点是B点,按照线状要素前进方向,其前一点是A点,后一点是C点。首先需要判断该点的凹凸性。按轴线方向可以得到该点之前的点和之后的点,与该点分别构成两个向量。由矢量代数可以知道,叉积的计算遵守右手法则。两向量AB和BC,
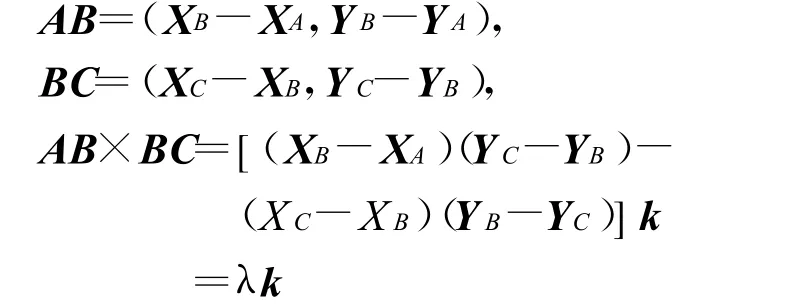
其中,k为垂直于AB和BC的单位正向向量向量积。即当 λ>0时,拇指朝上,该点为凸点;当 λ<0时,拇指朝下,该点为凹点;当λ=0时,三点共线。
若是凸点,则用半径为缓冲半径的圆弧段连接,方法类似于首端点缓冲区的生成,即用正n边形的部分边近似表示。其起始角度和终止角度的确定需要用两向量的数量积来确定。通过下面公式可以得到σ角,AB沿顺时针方向旋转到X轴所扫过的角度α,起始角度是α+3π/2,终止角度是α+3π/2+σ,其中每次增加角度2π/n。图2中对应凸点生成了线缓冲区边界多边形上C段上若干点。

若是凹点,首先判断该点是否是尖锐角。取得AB和BC两者中较小一个的长度L,AB和BC之间的夹角为β。如果L×tanβ/2大于半径值,是非尖锐角情况,否则就是按尖锐角情况处理。非尖锐角情况只需求出两段线段的右侧平行线的交点即可,将求出的点加入到结果点集中。右侧平行线可以根据已知线段的首末两点和线段方向及角度得出对应两点(这两点离原线段首末两点的距离为缓冲半径)。确定了平行线段的两点也就确定了平行线,从而得到两平行线的交点坐标,将其加入到结果点集中。图2中对应凸点生成了线缓冲区边界多边形上B点。如果是尖锐角情况所求点有三种情况,即是两弧段交点、弧段和延长平行线段交点或者两延长平行线段交点,如图3所示。这三种情况需要分情况判断,即用上文中所提到的判断一个点凹凸性的方法,分别做尖锐角两个边点的凹凸性判断。圆弧的生成类似于凸点的生成,该边沿顺时针方向旋转到X轴所扫过的角度α,起始角度是α+π/2,终止角度是α-π/2。平行线的生成类似于凹点非尖锐角情况,同时,因为在角度很小的情况下平行线段有可能在延长线上才可能与另一弧段(线段)相交,所以,需要将线段向两端延长若干倍数。这样得到两边的线段(弧段)坐标点(集),通过循环就可以得到交点坐标,将其加入到结果点集中。图2中对应凸点生成了线缓冲区边界多边形上D点。

图3 尖锐角情况
如果三点共线,则将中间点从线状目标中删除。
重复步骤2),直到线状目标的末端点。
3)线状目标的末端点的右侧缓冲区边界的方法和首端点的方法类似。
连接倒数第二个结点和末端点,形成向量AB。向量AB沿顺时针方向旋转到X轴正半轴扫过的角度为θ。起始角度是θ+3π/2,终止角度是θ+2π,其中每次增加角度2π/n。
4)将线状目标的顺序反转,重复上述步骤,就可以得到该线状目标的双侧缓冲区上所有的点。
5)这时得到的缓冲区点集中可能包含自相交的情况,需要进行自相交判断及处理。
该处理是一个双层循环的递归函数,在外层循环上,依次取的已得到的点集中相临的两点组成的线段,在内层循环上依次取外层循环确定的线段之后的相临两点。判断内外层两条线段是否相交,如果不相交则退出本次内层循环,执行下一次内层循环。如果相交则求出相交点,在交点处将原有的点集分割为两个点集,然后分别对这两个点集调用自相交处理函数。经过这样的处理,得到的是若干自相交多边形,需要判断多边形缓冲区的内外环。如果多边形是顺时针方向,则是岛屿多边形,构成缓冲区多边形的内环,如果是逆时针方向,则取其中面积最大的多边形作为缓冲区多边形的外环。
2.3 面缓冲区生成算法
面缓冲区生成算法是以线缓冲区生成算法作为基础。面状要素缓冲区生成可以分为面扩张缓冲区和面收缩缓冲区。面缓冲区生成算法可以按要素的单侧多边形进行处理,将生成的点集加上面的边界点,再进行自相交处理即为面状要素缓冲区。
2.4 相关算法
在上述算法中有很多算法都需要用到两线段相交算法,如自相交算法和尖锐角处理等。如果两线段相交算法失真或者低效对整个算法的影响较大。两线段相交算法中首先判断两线段的外接矩形是否相交,如果相交则继续判断两线段是否跨立。以两线段 AB和CD来说明跨立的计算。计算[(XC-XA)*(XC-XD)+(YC-YA)*(YCYD)]*[(XC-XD)*(XC-XB)+(YC-YD)*(YC-YB)],如果该值大于等于零则继续进行。接下来通过方程联立求得交点,并进行垂直、竖直等特殊情况的判断。这里要注意的是,在数据类型中精度是有限的,需要排除末位随机数对结果的影响。
3 缓冲区合并算法
通常需要处理的并非是单一目标,而预期结果是若干目标共同的缓冲区多边形。这就需要逐个实体生成缓冲区,然后进行缓冲区合并。合并以后可以得到一个整体的多边形或者若干个有共同边的多边形,这里就第一种情况进行讨论。上述算法解决了逐个实体的缓冲区生成,下面介绍缓冲区合并算法。经过第2节的处理,得到一个外环和若干个(或零个)多边形内环。这样在进行缓冲区合并的时候就要分为外环求并,内环求并以及内外环求差。
外环求交算法类似于自相交的处理函数。该函数中首先取两个多边形外环进行双层循环,在外层循环上,依次取第一个外环点集中相临的两点组成的线段,在内层循环上依次取第二个外环点集中相临的两点组成的线段。判断内外层两条线段是否相交,如果相交则求出相交点,在交点处将原有的点集分割为两个点集,然后分别对这两个点集调用自相交处理函数。经过这样的处理,得到的是若干自相交多边形,将其中最大的顺时针多边形加入到结果队列中。如果循环完毕后仍没有相交,将这两个外环都加入到结果队列中。然后依次取结果队列中的多边形与其他多边形循环。最后在结果队列中的多边形就是多目标缓冲区的外环。
内外环求差算法就是将一个缓冲区的内环与其他缓冲区的外环求差,求差结果就是缓冲区内环。具体算法就是首先判断内环与外环的外接矩形是否相交,如果相交则进行双层循环。首先判断内环第一个点是否在外环中,如果在外环中则判断下一个点,直到找到一个不在外环中的内环点,将其设为内层循环的起始点。内层循环依次取相临的两个点组成的线段,外层循环依次取外环上相临的两个点组成的线段。判断两条线段是否相交,如果不相交将内层循环第一个点加入到结果队列,如相交则将相交点加入到结果队列中。并将该点和下次相交点之间的外环点加入到结果队列中。
内环求并算法与自相交处理过程相同。
4 结 论
该算法在目标很小缓冲区半径很大的情况下效果有待改善。另外在自相交检查时,在多目标自相交情况较多的情况下效率有待提高,应考虑使用检索方式提高效率,即用网格将整个区域划分为若干小的网格,在小的网格内判断自相交。这是下一步所考虑实现的内容。
该算法考虑了含有内环的多边形的缓冲合并情况,并对一些特殊情况如尖锐角的情况进行了讨论。上述算法已经编程实现,经过测试算法可以满足用户对缓冲区生成的要求。
[1] 黄杏元.地理信息系统概论[M].2版.北京:高等教育出版社,1989:130-131.
[2] 刘湘南,黄 方,王 平,等.GIS空间分析原理与方法[M].北京:科学出版社,2005:104-107.
[3] 张成才.GIS空间分析理论与方法[M].武汉:武汉大学出版社,2006.
[4] 毋河海.关于GIS中缓冲区的建立问题[J].武汉测绘科技大学学报,1997,22(4):358-364.
[5] 陈学工,张文艺,张弛伟,等.一种GIS缓冲区矢量生成算法及实现[J].计算机技术与发展,2007,17(3):13-16.
[6] 董 鹏,毛东军,李 军,等.一种有效地GIS缓冲区生成算法[J].计算机工程与应用,2004,40(16)4-8.

