应用 EXCEL电子表格编制大地网转换程序
谭 君,陈尚云
(四川中水成勘院测绘工程有限责任公司,四川 成都 610072)
1 前 言
任何一个国家大地控制网的建立,都有一个历史的发展过程。在不同的时期采用的参考椭球及定位方式都不会相同,并总是逐步完善和精密化,因此就存在不同精度等级大地网的转换问题。以我们国家为例就有 1954年北京坐标系、1980西安坐标系以及现在推行的 2000国家大地坐标系。
在工程建设中,也经常存在不同坐标系的转换问题,如将国家坐标系的坐标转换为地方坐标系或工程坐标系的坐标等等。
解决坐标转换有两种方法,一是严密法,二是近似法。所谓严密法就是将旧的全部观测值在新坐标系中重新平差,算出各点的新坐标值。本文介绍的近似法是在旧资料不足或其它工程急需的情况下采用的一种方法。近似法要求新旧网中必须有足够的同名点用以解算新旧坐标系之间的转换参数,当同名点个数大于基本要求时采用最小二乘法求解。
2 坐标系转换的数学模型
坐标系转换数学模型有正形变换模型、仿射变换模型和赫尔默特变换模型。
正形变换模型的数学公式如下:

实际应用时计算至 P4、q4就可以了。由于每个重合点可以列两个误差方程,因此正形变换法进行坐标转换时最少需要 5个重合点。
仿射变换模型的数学公式如下:
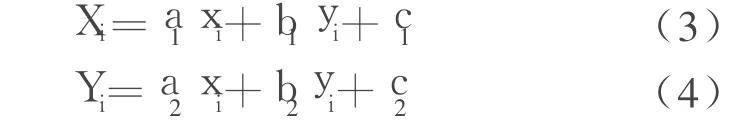
赫尔默特变换模型的数学公式如下:
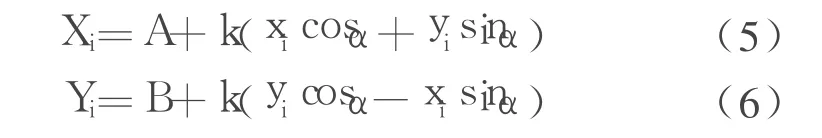
上述式中 X、Y表示新坐标系中的坐标;x、y表示旧坐标系中的坐标;Pi、qi表示正形变换中的各个变换参数;ai、bi、ci表示仿射变换中的各个变换参数;A、B表示赫尔默特变换中新旧坐标系之间的平移参数;k表示赫尔默特变换中新旧坐标系之间的缩放数;α表示赫尔默特变换中新旧坐标系之间的旋转角度。
3 程序编写
现以正形变换为例叙述程序的编写(本程序是在office-2003版 EXCEL电子表格中编写和运行)。
第一步:解求重心坐标,使用的函数为 AVERAGE(),把所有点的成果归化为重心坐标系的成果;
第二步:组成误差方程,按照公式(1)、(2)每点组成两个误差方程;
第三步:组成法方程,按照最小二乘法的原理组成法方程;
第四步:解法方程,使用函数 minVERSE()和MMULT();
第五步:求转换点新坐标,使用函数 MINVERSE()和 MMULT()。
为了使程序条理清晰便于使用,将整个程序分为四个工作表编写:第一个表是使用说明;第二个表是原始数据;第三个表是模型解算;第四个表是转换点计算。
本程序的特点是只要参加模型解算的点数大于5个,总点数(模型解算点 +待求点)-2≤电子表格的行数,就能一次性自动解算完毕。

图1 控制点布置
4 算 例
下面以 24个点组成一组正形变换算例说明程序的使用,点位分布见控制网布置图(图 1)。
第一例中参加模型解算的点数为 24个,待求点是 7个,从表中看出 24个点解求的模型内符合精度 mx=9.0(mm),my=13.2(mm)(见表1)。
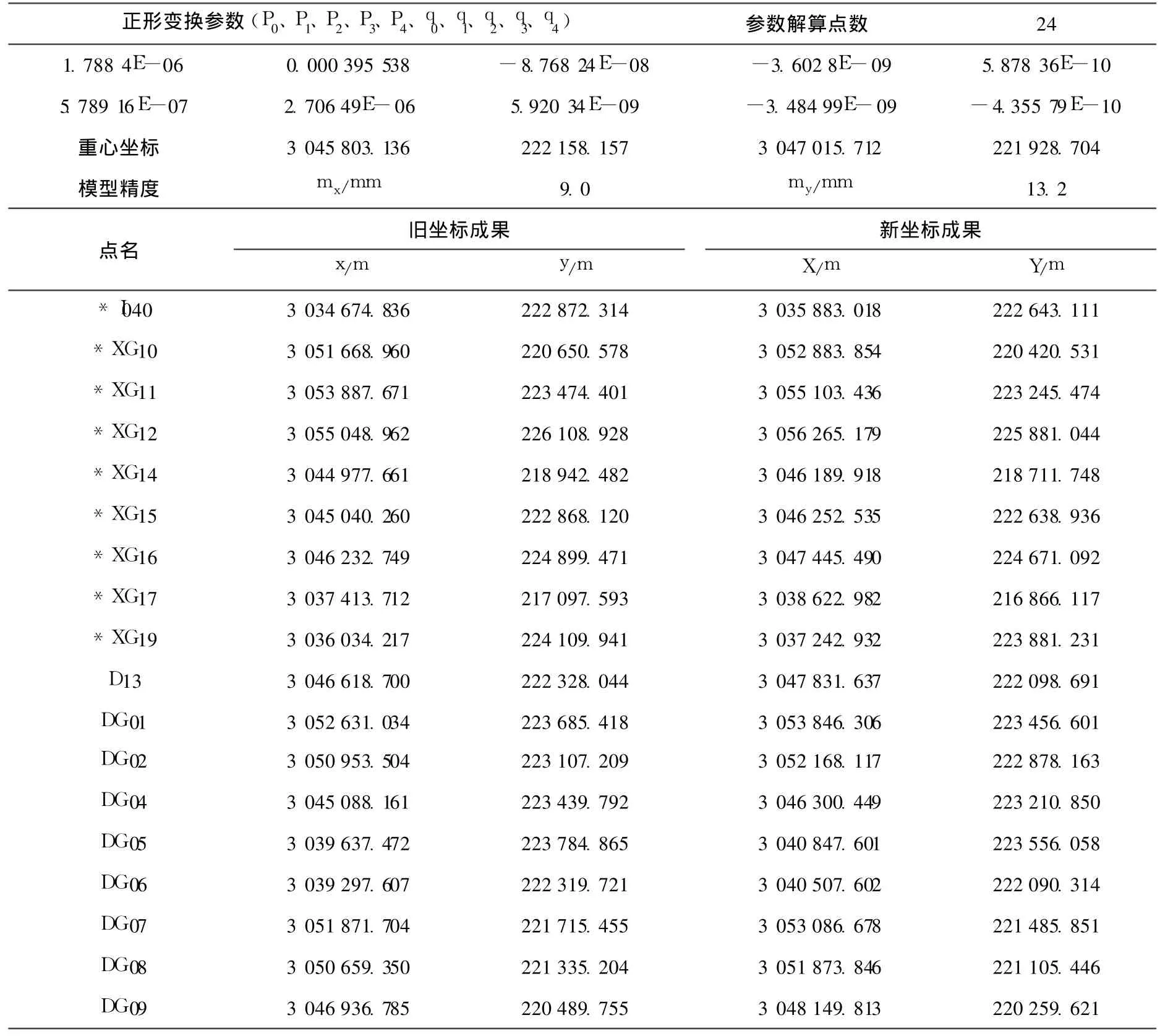
表1 不同系统间的坐标正形变换模型

续表1
第二例中参加模型解算的点数为 5个,待求点是 19个,由于模型解算无多余条件,所以内符合精度为 0(见表2)。
第三例中参加模型解算的点数为 8个,待求点是 16个,从表中看出 8个点解求的模型内符合精度 mx=5.1(mm),my=7.6(mm)(见表3)。
表4~6是三种模型解算的转换点坐标与已知坐标比较。
三个模型解算转换点成果较差见表7。

表2 不同系统间的坐标正形变换
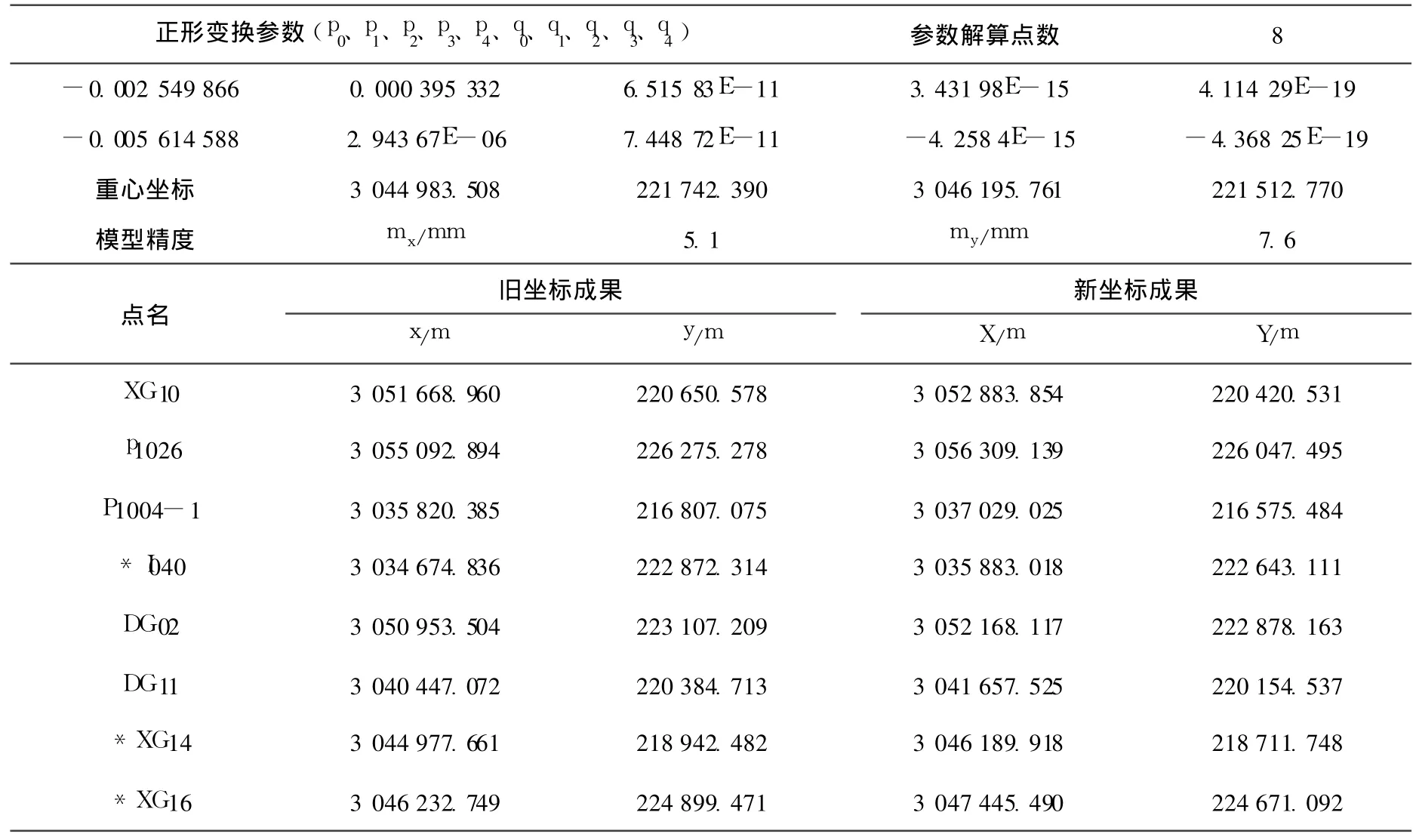
表3 不同系统间的坐标正形变换
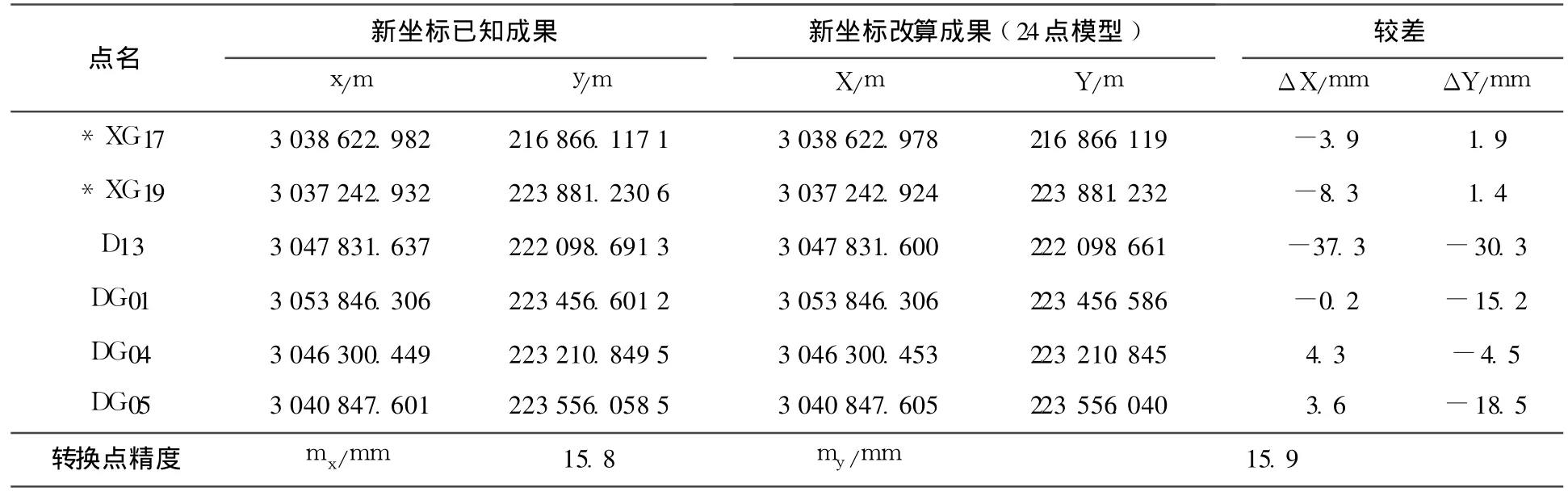
表4 24点模型改算点坐标的比较

表5 5点模型改算点坐标的比较

表6 8点模型改算点坐标的比较
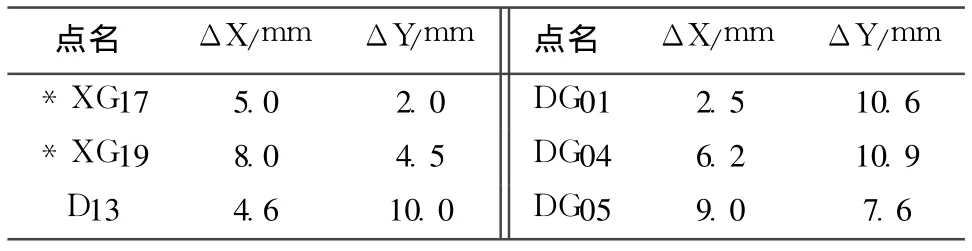
表7 三个模型解算转换点成果较差
5 结 论
从表4~6的转换点精度及表7的转换点成果较差分析可得出以下几点结论:
(1)模型解算点应均匀分布于整个转换区域,未知点应在模型解算点的控制范围内。
(2)当重合点的精度一定时,增加模型解算点数意义不大。
(3)本程序操作简单,界面友好,换算后得到的成果与专业测量平差软件得到的成果毫无差异。
(4)从正形变换的公式可知本程序也可用于仿射变换和赫尔默特变换,只是重合点数不能少于 5个,而仿射变换最少只需要 3个重合点,赫尔默特变换最少只需要 2个重合点。
(5)程序正确性验证算例(理论数据)见表8。
从验算模型可知程序是完全正确的,因为理论数据的内符合精度为 0mm。
[1]徐绍铨,吴祖仰主编.大地测量学[M].武汉:武汉测绘科技大学,1988.
[2]於宗俦,鲁林成.测量平差基础(增订本)[M].北京:测绘出版社,1983.
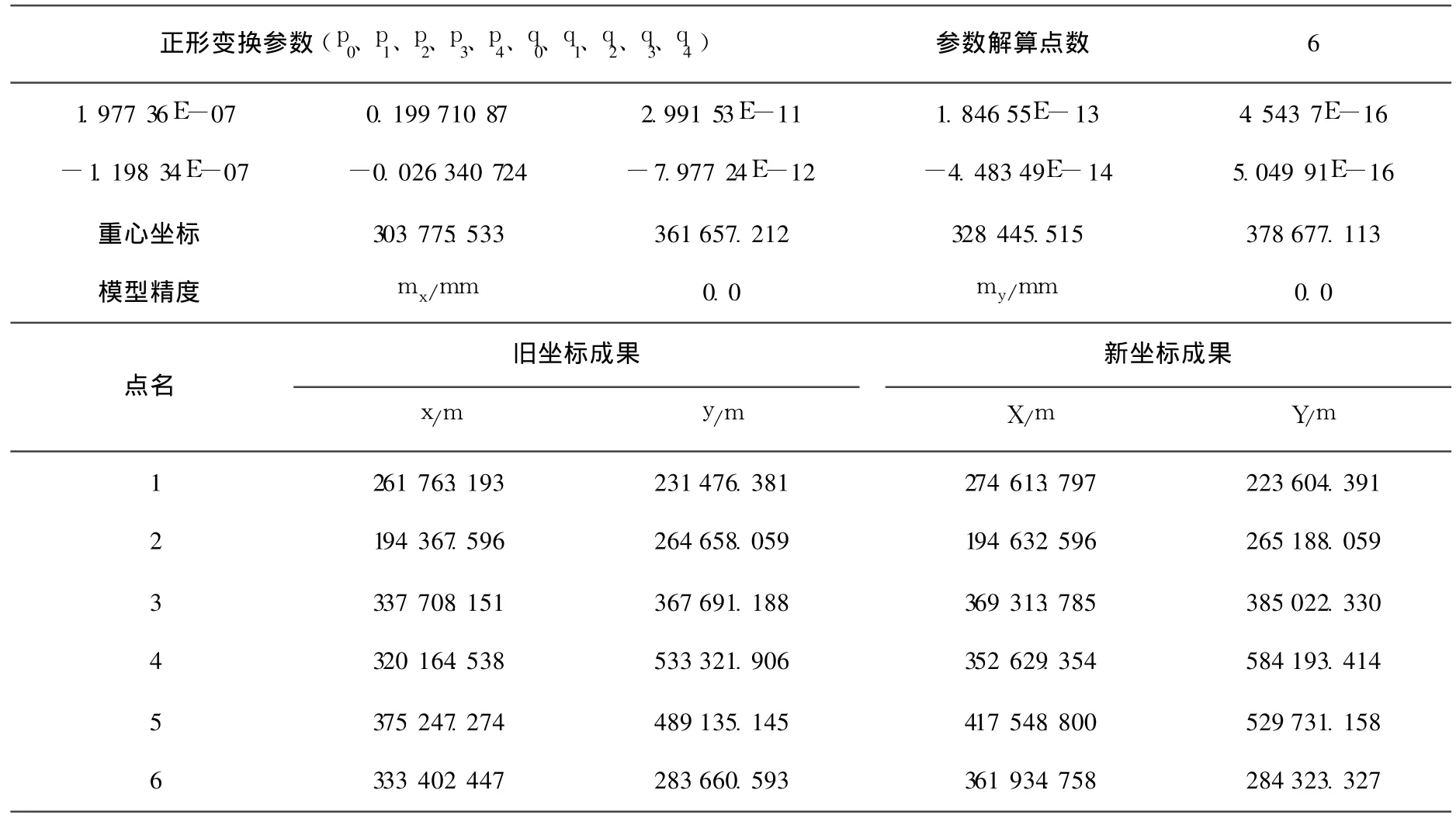
表8 不同系统间的坐标正形变换

