基于排队论的港口泊位服务系统优化仿真研究

王 健，胡碧琴（上海海事大学，上海 200127）

随着经济的一体化、全球化和市场经济的不断完善，中国国民经济和对外贸易得到迅速发展，港口业也进入快速增长期，港口货物吞吐量一直保持增长态势。2009年，中国规模以上港口完成货物吞吐量76.57万t，同比增长9.0%。其中，沿海港口完成48.74万t，同比增长8.6%；内河港口完成27.83万t，同比增长9.9%。随着国际贸易的迅速发展，港口吞吐量逐年上升，中国很多港口出现了拥挤现象。在中国港口吞吐量迅速发展的同时，许多港口码头能力严重不足的矛盾也日渐突出，实际完成的吞吐量常常要大于码头的通过能力，码头处于超负荷运行状态。摆在港口面前的重要问题是，在现有的码头规模下，如何尽可能地提高码头作业效率，充分挖掘码头的潜力，以满足港口吞吐量快速增长的需求。

1 泊位服务系统的特征

1.1 泊位服务系统是随机服务系统，船舶到港具有随机性

目前，航运市场上存在着租船运输、班轮运输等多种运输方式。租船运输挂靠港口的不确定性以及班轮在航行过程中易受风、浪、流的影响而不能保持恒定的航速，导致船舶无法按规定的时间到达港口。港口作业同样具有随机性。在港口生产营运过程中，易受气候条件、装卸能力、管理调度水平等许多因素的影响而不能准确地确定船舶的在港时间。

1.2 泊位服务系统是离散事件系统

泊位服务系统的状态变化只在时间的离散时刻发生，呈状态突变，是随机的离散事件系统，其动态特性需用一组离散状态方程来描述。船舶到达港口、进入锚地排队、离开锚地、靠近泊位、开始作业、作业结束、离开港口等事件均发生在时间的离散时刻，并具有随机性。

1.3 泊位服务系统是排队系统

由于港口作业的随机性和来港船舶的随机性，使得港口营运具有很大的不平稳性。在港口营运系统中，一个码头泊位在同一时刻只能为一艘船舶服务，并且要求码头泊位的靠泊能力不小于船舶的吨级，装卸的货种与船舶的类型一致，因此每种货物的装卸与转运是一个相对独立的子系统，船舶必须按类型排队，形成排队系统。

2 港口泊位服务模拟系统

港口泊位服务系统的模拟方案设计是根据港口实际情况，通过模拟的方法模拟影响因素发生变化时，对港口泊位服务系统服务质量的影响，由此分析最经济有效地提高泊位服务系统能力的方法。利用计算机模拟对港口运营进行模拟，是针对实际港口情况，模拟港口的运行状况，获得有关的港口数值特征值。

仿真系统的研制设计遵循以下基本原则：

2.1 系统模型应符合港口实际

只有建立切合实际的系统模型，才能得到合理可信的结果。因此在港口服务系统的模拟模型设计中，必须使系统的服务模式、船舶的排队模式及各随机变量的概率分布模型等尽量与实际情况一致，保证模型能够反映港口实际运营情况。

2.2 系统条件参数应可调

港口码头泊位的数量及属性（装卸效率等）、船舶平均到达率、各类来港船舶的类型分布，必须能够方便地进行修改和调整。本文以某港2009年到港船舶的相关数据为基础，并用excel对其泊位服务系统进行模拟优化研究。

3 港口泊位模拟服务系统

3.1 具有一个泊位的港口系统模拟

3.1.1 实际问题与数据

某港口只有一个可供装卸的泊位，但供船舶等待的泊位无限制。当船舶到达港口时，如果泊位内已有船舶，则需排队等待，排队的规则是先到先服务。根据100艘船舶来港口停泊的记录，它们到达港口的时间间隔分布和装卸时间分布分别用图1和图2的频数直方图表示。在图1中，横坐标为船舶到达时间间隔，纵坐标为具有不同到达时间间隔的船舶数（频数）；在图2中，横坐标为装卸时间，纵坐标为具有不同装卸时间的船舶数（频数）。

3.1.2 用excel进行模拟

船舶到港后，排队进入码头进行装卸，然后离开码头。服务台是泊位，这是一个单服务台排队问题。其中，不可控变量有两个，一个是船舶到达时间间隔，另一个是装卸时间。首先用随机数产生不可控变量的抽样值，然后对该系统进行模拟，最后得到关于该排队系统的性能指标的统计量。

（1）输入已知数据

首先在excel的工作表上输入已知数据（见表1）。由图1和图2可得到船舶到达的时间间隔和装卸时间这两个不可控变量的概率分布及其对应的随机数区间。

（2）模拟运算

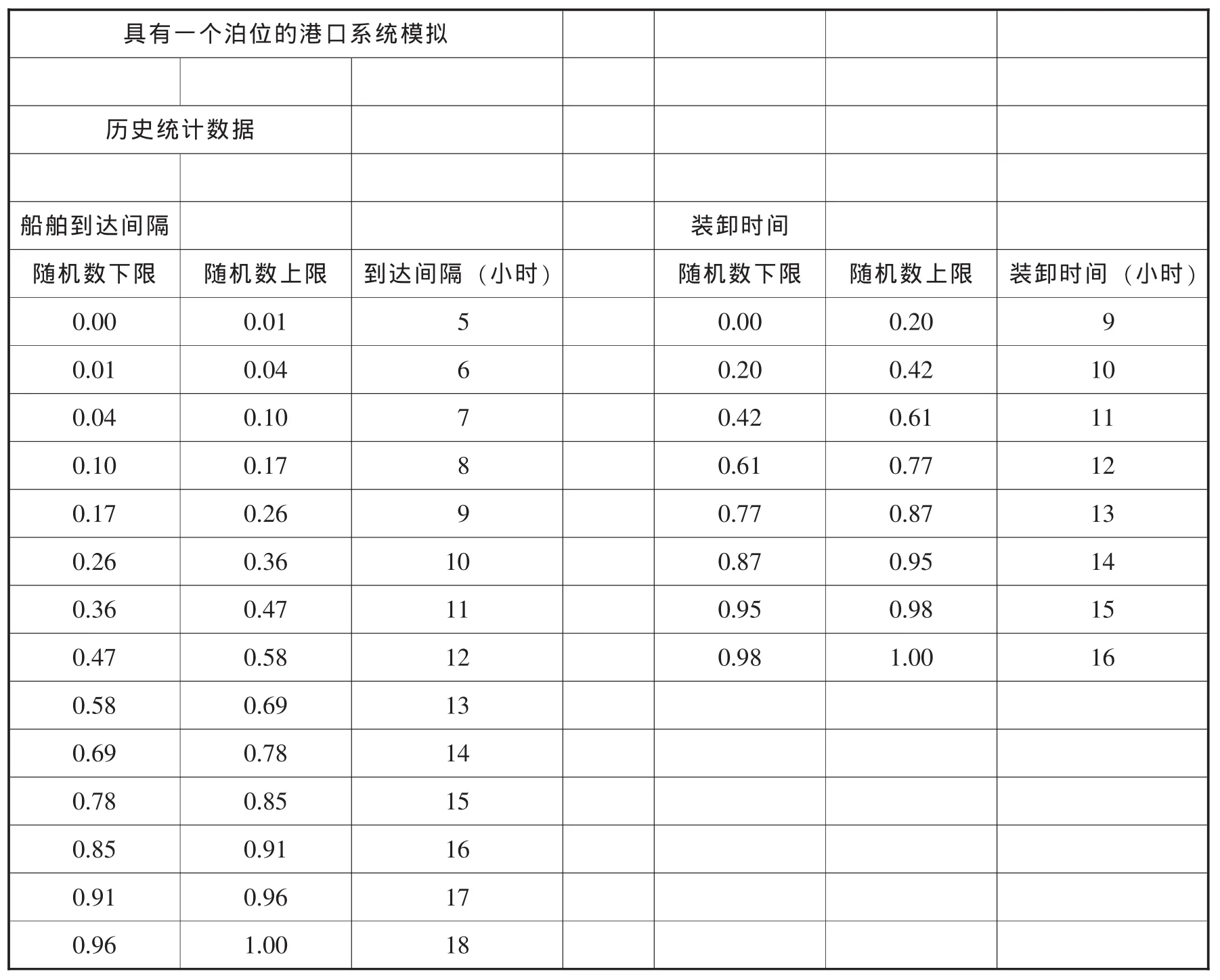
表1 输入已知数据

下面对泊位排队系统进行模拟（见表2）。泊位排队系统的主要过程是：

a.船舶到达；

b.当泊位空闲时船舶立即开始装卸，当泊位不空闲时船舶排队等待，直到泊位有空闲时开始装卸；

c.完成装卸，船舶离港。

（3）统计分析

对泊位进行了1 000次模拟，得到了1 000艘船舶的模拟运算结果。下面是对运行结果进行的统计分析。由于在模拟开始时泊位是空闲的，所以，前若干艘船舶的模拟结果往往不能确切反映泊位达到稳定工作状态时的行为，为此，在进行结果分析时，不计前100艘船舶的运行结果，而仅对后900艘船舶的运行结果进行统计分析。统计结果见表3。

3.1.3 模拟结论

根据模拟结果可作出如下分析：

（1）当前具有一个泊位的情况下，泊位利用率高达94.39%，船舶的平均等待时间为7.61小时，其中有24.22%的船舶需要等待10小时以上才能开始装卸。所以，可能造成失去部分客户。

（2）当前的情况难以满足日益增长的运输需求。但是否需要增加泊位，以及应增加多少泊位，则还需进行增加泊位后的模拟。

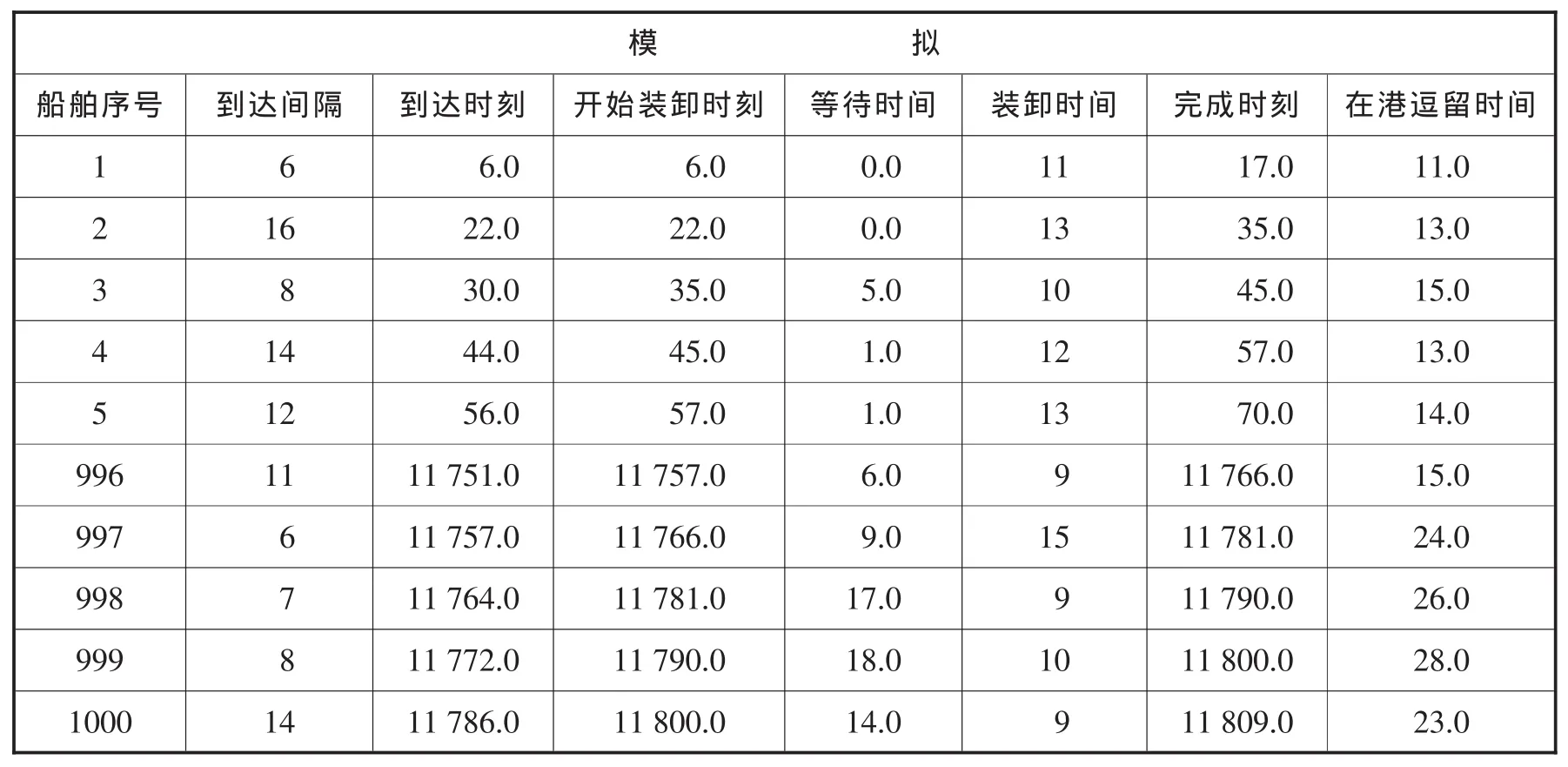
表2 具有一个泊位的港口排队系统模拟模型

表3 具有一个泊位的港口排队系统模拟的统计结果

3.2 具有两个泊位的港口系统模拟

在3.1中，由于船舶等待时间过长，港口考虑增加一个泊位，用模拟方法研究该港口排队系统具有两个泊位时的性能。

当港口有两个泊位时，情况要比只有一个泊位时复杂得多。这时排队系统的主要过程是：（1）船舶到达港口；（2）当两个泊位均为空闲时，船舶进入其中一个泊位并立即开始装卸；当只有一个泊位空闲时，船舶进入该泊位并立刻开始装卸；当两个泊位均不空闲时船舶排队等待，直到有一个泊位空闲时开始装卸；（3）完成装卸，船舶离港。

3.2.1 用excel模拟两泊位系统

两个泊位时的港口排队系统模拟模型与一个泊位时相比，其到达时间间隔、到达时刻、等待时间、完成时刻、在港逗留时间的计算方法都相同，两者的主要区别在于：

（1）开始装卸时刻的计算

a.船舶开始装卸时间=船舶到达时刻，船舶到达时刻＞泊位最早开始空闲时刻；

b.船舶开始装卸时间=最早开始空闲时刻，否则

（2）每个泊位的“开始空闲时刻”的计算

泊位1的开始空闲时刻=

a.本次装卸完成时刻，上次泊位1开始空闲时刻＜=上次泊位2开始空闲时刻；

b.上次泊位1开始空闲时刻，否则

泊位2的开始空闲时刻=

a.本次装卸完成时刻，上次泊位1开始空闲时刻＞上次泊位2开始空闲时刻；

b.上次泊位2开始空闲时刻，否则

根据以上分析，得到两泊位港口系统模拟模型如表4：

表4 两泊位港口系统模拟模型

3.2.2 统计分析（见表5）

表5 两泊位港口系统模拟模型的统计结果

3.2.3 分析结果

当该港口的泊位增至两个时，泊位利用率下降到47.29%，船舶的平均等待时间仅为0.01小时，在900艘船舶中只有4艘需要等待，其中只有1艘船舶的等待时间超过3小时。可见这时与一个泊位时相比，服务水平有明显改善。

模拟结果表明，在当前的需求水平下，拥有两个泊位，已经可以满足运输需要，但是泊位利用率略低，不过考虑到日益增长的运输需求，增加一个泊位是一个可取的方案。但是否需要增加泊位，还需要进一步的论证，例如进行可行性分析、财务分析与经济分析等。

4 结论与建议

排队模拟模型可以较好地应用于泊位系统规划中，借助于实际数据，解决为不同种类的集装箱船舶安排几个泊位，以及分析建设多少泊位比较经济等泊位分配问题，具有较强的实际应用价值。

[1]丁以中，Jennifer.S.Shang.管理科学——建模及实例分析[M].北京：清华大学出版社，2003.

[2]唐应辉，唐小我.排队论：基础与分析技术[M].北京：科学出版社，2006:18-30.

[3]张铭强，商剑平，王诺.计算机模拟在港口规划中的应用[J].水运工程，2005(2):33-36.

[4]张丽君，侯超惠，胡国强,等.现代港口物流[M].北京：中国经济出版社，2005:24-36.

[5]杨宏.港口生产系统方案设计仿真研究[D]．上海：上海海事大学（硕士学位论文），2006:5-8.

[6]蔡临宁.物流系统规划——建模及实例分析[M].北京：机械工业出版社，2003.