钢管混凝土拱连续梁桥的动力特性分析

唐 志，马晓锋，杜 镔，陈冠桦，丁作常

(贵州省交通规划勘察设计研究院，贵州 贵阳 550001)

随着桥梁跨度的不断增大，以及桥梁发展日趋轻薄型，大跨度钢管混凝土拱连续梁桥的抗震、抗风以及车辆荷载的冲击振动等许多动力问题越来越引起人们的关注。桥梁的动力性能主要取决于桥跨结构的组成体系、各构件的刚度、质量分布以及支撑条件等因素，因此对钢管混凝土拱桥进行参数分析，能够更好地了解不同参数对此类桥型动力性能的影响，从而可以合理地指导该类桥型结构的设计，对该类铁路桥梁的提速加固等都有指导意义。

1 工程概况

本文以某钢管混凝土拱连续梁桥为例进行了分析，该桥主跨跨度180 m，边跨梁长90 m，桥型布置如图1。拱肋中心距采用11.9 m。拱的计算跨径L=180 m，设计矢高f=36.0 m，矢跨比f/L=1/5，拱轴线为抛物线。主跨拱肋采用等高度哑铃形截面，拱肋高3.10 m，弦管外径1.10 m。两拱肋间共设9道横撑，横撑采用500×14 mm和250×10 mm空钢管。主梁采用单箱双室截面，中支点梁高10.0 m，主跨跨中及边支点梁高4.5 m。全桥共设18组双吊杆，吊杆间距9.0 m，吊杆采用PES(FD)7－61型低应力拉索(平形钢丝束)，其 fpk=1670 MPa，Ep=2.0 ×105MPa。

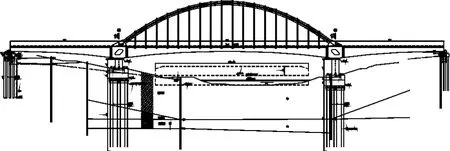
图1 桥型布置图

2 有限元模型及荷载简介

由于桥梁自振特性取决于结构的组成体系、刚度、质量分布以及约束条件等，所以计算模型的模拟关键在于结构的刚度、质量和边界条件的模拟。结构的刚度模拟主要指杆件轴向刚度、弯曲刚度、剪切刚度和扭转刚度的模拟，有时包括翘曲刚度和杆件间连接刚度的模拟等;结构的质量模拟主要指杆件的平动质量和转动质量的模拟;边界条件的模拟应和结构的支承条件相符。这三个主要因素直接决定了结构的动力特性。

钢管混凝土拱桥的结构比较复杂，本文用有限元建立桥梁模型，对于拱肋、主箱梁、桥墩、横撑采用空间梁单元建模。由动力学势能驻值原理及形成矩阵的“对号入座”法则，建立桥梁刚度、质量、阻尼矩阵，从而得到动力平衡方程。有限元模型如图2。

图2 全桥有限元模型

3 动力特性分析

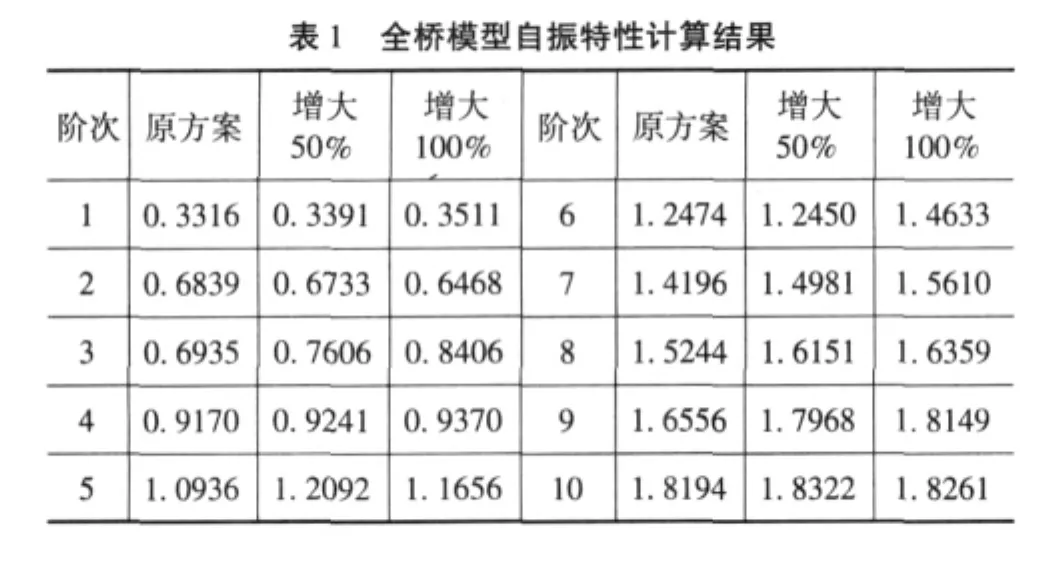
自振频率是反映桥梁结构刚度和质量的指标，它是桥梁结构进行动力分析的基础。主振型决定了结构动力响应状态的发生。根据上述桥梁计算模型，利用子空间迭代法求解桥梁前十阶自振频率及其振型，并描述了其相应的振型特征。

从表1可以看出:对于该钢管拱桥系杆拱桥，拱肋面外振型出现的最早，面外刚度弱于面内刚度，面内与面外的振动基频分别为1.2474和0.311，二者的比值为4.0。显然，桥跨结构面外横向振动影响要大于面内竖向振动影响，这也是钢管混凝土拱桥结构的共性所在。相对于公路桥梁来说，铁路桥梁的宽跨比较小，因此，该类桥梁的横向刚度问题表现的更为突出。

?

4 桥梁动力特性影响因素分析

由于钢管混凝土系杆拱桥是一种柔性结构，横向刚度弱，因此，在设计中，在一般设置考虑设置横撑以增强其横向稳定性。而拱肋作为桥梁的主要承重构件，拱肋的材料特性、截面形式和尺寸对桥梁自振特性有着重要的影响。以下分别从变更横撑，改变拱肋截面的尺寸和材料，更改约束条件等来探讨钢管混凝土拱连续梁桥的自振动力特性。

4.1 横撑布置对桥梁动力特性的影响

不改变横撑的材料特性和截面尺寸，现考虑以下几种模型:

方案1:去掉所有横撑，成敞口拱;

方案2:仅去掉两拱脚处两根横撑，保留中间5根横撑;

方案3:仅保留拱脚处两根横撑与拱顶处横撑，去掉中间4根横撑;

方案4:全桥设置9道横撑(原方案)。

?

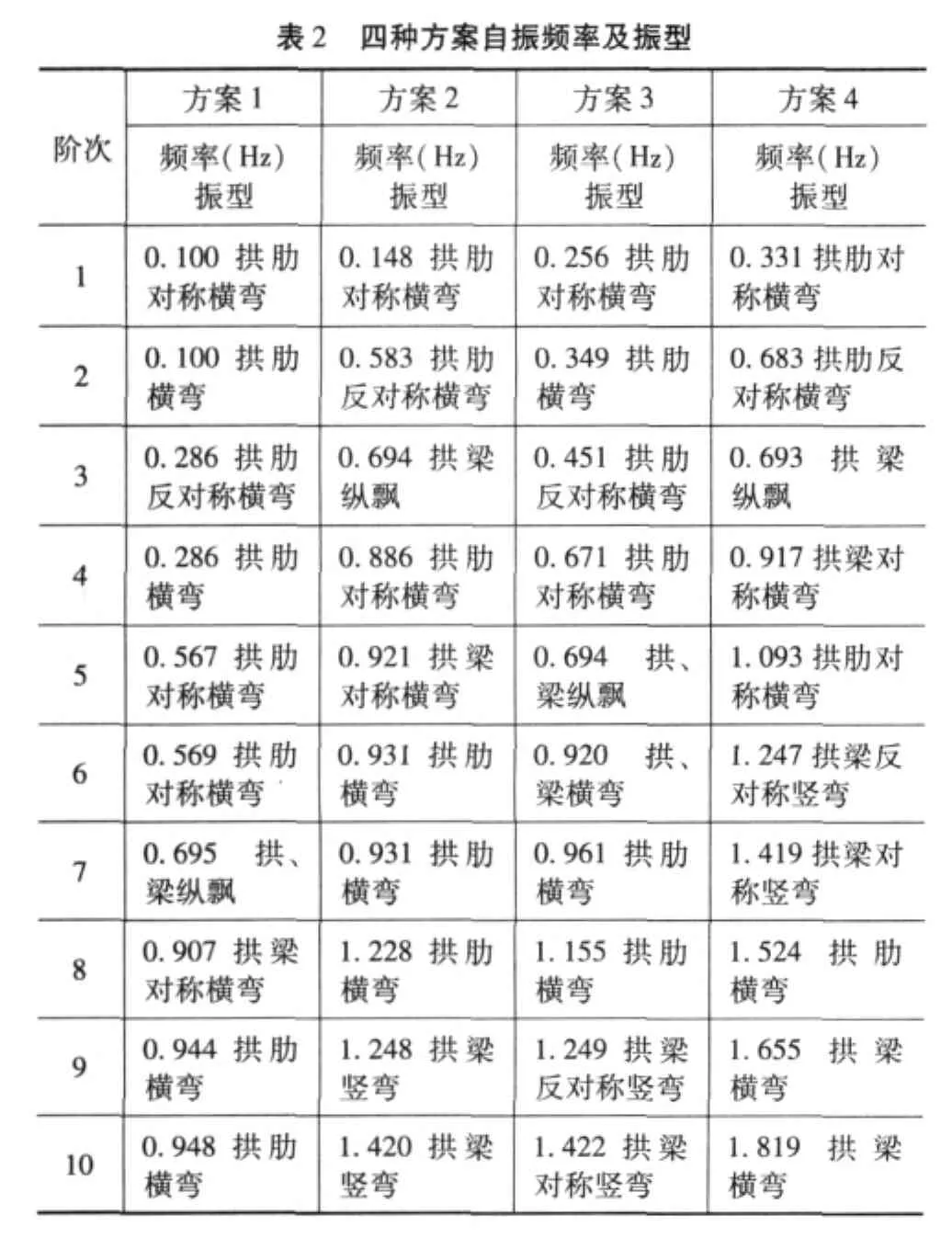
由计算结果可知:

(1)从方案1到方案4，桥梁的第一阶振型均为拱肋对称面外弯曲，说明其横向刚度比较弱，其自振频率分别为0.100，0.148，0.265，0.331 可见，随着横撑的增加，自振频率不断变大，说明横撑的设置可以明显提高钢管混凝土的横向刚度。方案2和方案3的自振频率为0.148和0.265，同时也说明对于本桥横撑布置在拱顶和1/4拱肋处时对桥梁的横向刚度贡献更大。

(2)对比桥梁的竖向基频和纵向基频可知，增减横撑和改变横撑位置对其影响不明显，纵向和竖向基频的数值没有发生任何变化(纵向为0.69左右，竖向为1.25左右)，说明横撑对桥梁的纵向和竖向刚度的影响可以忽略。

(3)横撑的多少和布置，还可以改变振型的次序和形状。

对于方案1，前五阶均为横向振型，而且横向基频最小，说明桥梁的横向刚度最弱。第6阶才开始出现纵向振型，竖向振型出现在第11阶;方案2在第3阶就出现了纵向振型，竖向振型出现在第9阶;方案3在第5阶就出现了纵向振型，竖向振型出现在第9阶;方案4在第3阶就出现了纵向振型，竖向振型出现在第6阶。可见，横撑的布置对桥梁的自振特性的影响较大。

综上所述，横撑的布设对全桥动力特性是有较大影响的。加设横撑，能显著提高全桥面外刚度;横撑设置位置对桥梁横向刚度也有影响，对于本桥来说，在横撑布置在拱顶和1/4拱肋处时对桥梁整体面外刚度贡献要大。

4.2 主拱肋对桥梁动力特性的影响

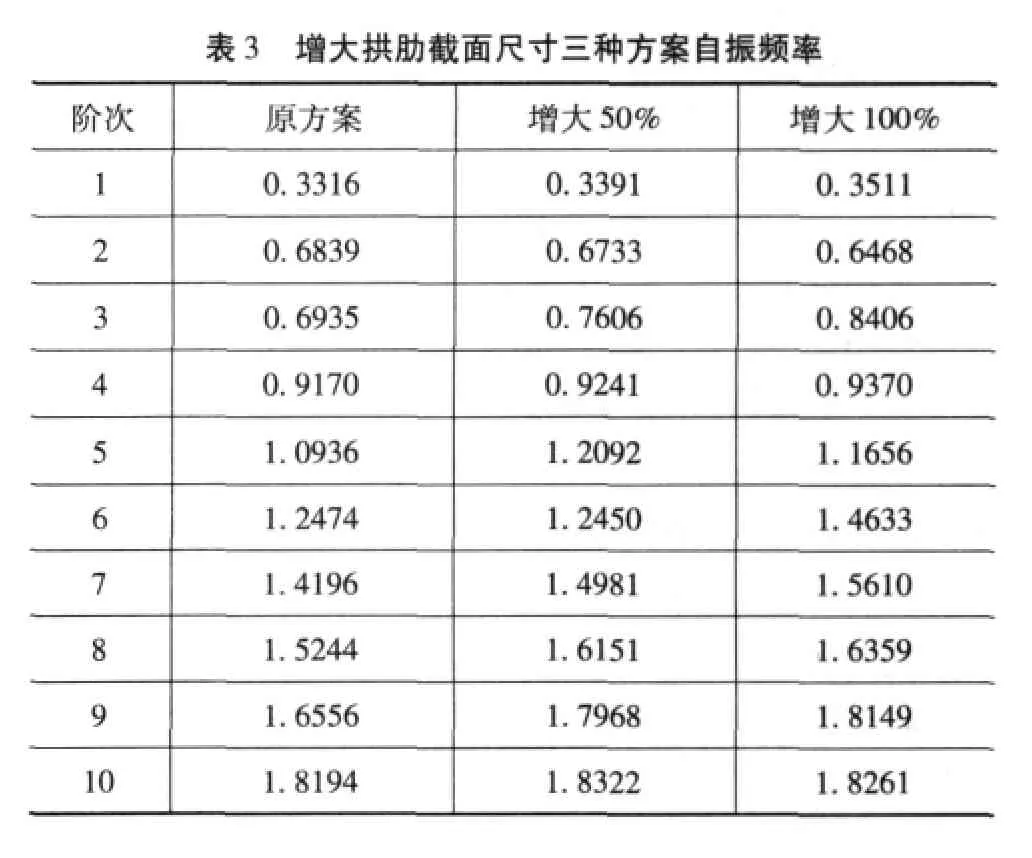
保证钢管材料性质不变，且钢管的含钢率保持不变，增大钢管的直径探讨以下几种方案。

由表3可以看出，随着拱肋截面的增大，桥梁的自振频率不断增大。当拱肋截面增大一倍时，其横向基频增大为13%，说明适当增大主拱肋的截面，能有效提高全桥自振频率。

?

4.3 约束条件对桥梁动力特性的影响

原模型的约束条件为:两拱肋固结，而两边墩采用铰接(约束横向和竖向线位移)，中墩采用单排支座，约束横向和竖向位移，约束一中墩的纵向线位移。考虑桩－土的弹性约束。在原模型的基础上对以下几种情形 进行了探讨:

(1)原模型约束边墩方式不变，两中墩采用双排支座即约束横向转角;

(2)在原模型约束基础上，约束两中墩的纵向线位移。

根据计算结果，对比模型1与原始模型，纵向频率影响明显，由0.6935增大到0.8642，增大了近25%，主要是由于两中墩采用了双排支座，约束了横桥向的转角，增大了两中墩对桥梁纵向刚度的贡献;对于横向刚度没有影响，竖向频率也略有变化，说明采用双排支座可使桥梁的整体刚度得到提高。对于本桥来说，从动力特性方面考虑采用双排支座要优于单排支座。

模型2对比原始方案约束两中墩的纵向线位移，这样使得桥梁的纵向频率增大，从0.6935增大至0.9170，增幅达32%，说明显著地提高了桥梁的纵向刚度。说明对桥梁的竖向刚度也有所贡献。

5 结论及建议

本文通过对钢管混凝土拱连续梁桥的动力特性分析，提出如下结论和建议:

(1)钢管混凝土拱连续梁拱桥跨结构面外横向振动影响要强于面内竖向振动影响，桥梁的横向刚度问题很突出，应引起重视;

(2)变化设计参数可以发现，横撑位置和数目的变化对钢管混凝土拱连续梁桥的自振特性有较大影响，跨中和1/4拱肋附近的影响更为明显，适当增加横撑数目可以有效地提高结构的面外刚度。主拱肋刚度的变化对该桥整体刚度影响较大，各振型的频率值随拱肋刚度的增大而明显增大;

(3)从动力性能方面考虑，对于钢管混凝土拱连续梁桥设置双排支座要优于单排支座。

［1］曾庆元.弹性系统动力学总势能不变值原理［J］.华中理工大学学报，2001，28(1)

［2］李国豪.桥梁结构稳定与振动［M］.北京:中国铁道出版社，1996

［3］陈宝春.钢管混凝土拱桥设计［M］.北京:中国铁道出版社，2001

［4］程海根，强士中.钢管混凝土提篮拱动力特性分析［J］.公路交通科技，2002，19(3):63 －65

［5］陈盛水，陈宝春.钢管混凝土拱桥动力特性分析［J］.公路，2001(2):10－14