基于移动最小二乘拟合大跨结构动载实验冲击系数分析

龙建旭，石东艳

(1.贵州交通职业技术学院，贵州 贵阳 550008;2.贵州大学土木建筑工程学院，贵州 贵阳 550008)

随着我国经济建设的高速发展，社会工业化水平提高，不仅车辆数量急剧增加，车辆重量增大，而且车速也相继提高，人们对道路的服务水平提出了新的要求。近20年来，尽管我国开始了对旧桥加固技术的研究，但由于旧桥数量庞大，加上20世纪80年代以后建设的桥梁随着运营年限的增加，也逐步进入了维修养护期，缺陷和病害开始显现发展。特别是大型、重型车辆与日俱增，超限、超载车辆越来越多，对桥梁的损伤和破坏日趋严重，大批桥梁又加入维修、动载试验通过测试桥梁在动荷载下的响应，通过分析动力响应和模态参数(频率、阻尼和振型)对桥梁承载力进行评定。

冲击系数计算时候常采用在汽车过桥时测得的效应时间历程曲线上，最大静力效应处量取的最大静力效应值与在效应时间历程曲线上最大静力效应处量取的最大动效应值进行比较得出。从时间历程曲线上读取最大动力效应值较为容易，但最大静力效应值往往为近似读取。因此常常带来较大误差。本文通过对某大桥进行动载试验，取了桥梁结构的基频、振型等动力响应参数，了解结构冲击荷载的动力特性。在计算冲击系数计算时候引入最小移动二乘法，使得拟合的效应时间历程曲线更加光滑，将计算误差降到最低。

1 移动最小二乘近似

在移动最小二乘(MLS)近似中，函数近似的形式为:

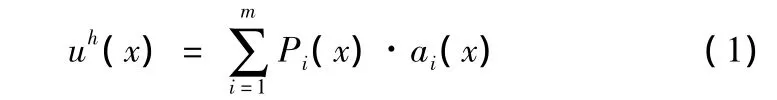
式中:m是基函数的个数，Pi(x)是基函数，ai(x)是相应的系数，并且它是空间坐标的函数。通常使用单项式作为基函数，当然，也可以使用任何其它函数。系数ai(x)的确定是根据加权最小二乘原则，要求对函数的局部近似误差最小。即:

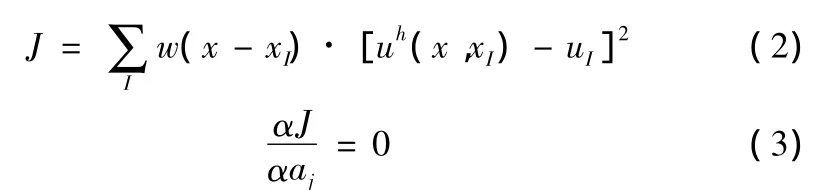
根据上式可求得系数 ai(x)，从而可建立 MLS的近似式:

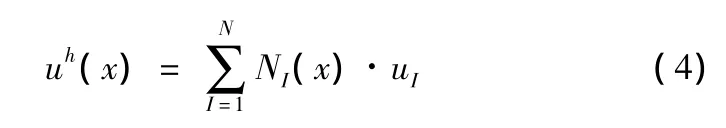
移动最小二乘近似能保证数值方法的收敛性与稳定性，由于其“局部”性质使得得到曲线更为光滑，并且能使曲线的导数曲线连续。

2 冲击系数

冲击影响与结构的刚度有关。一般来说，跨径越大、刚度越小对动荷载的缓冲作用越强，以往规范近似地认定冲击力与计算跨径成反比(直线变化)，无论是梁式桥还是拱式桥等，均规定在一定的跨径范围内考虑汽车荷载的冲击力作用。结合公路桥梁可靠度研究的成果，采用了结构基频来计算桥梁结构的冲击系数。汽车荷载的冲击系数可表示为:

当f＜1.5 Hz时，μ=0.05 当1.5≤f≤14 Hz时，μ=0.1767lnf－0.0157

当f＞14 Hz时，μ=0.45 (本论文中频率f采用桥脉动实验所得到的3.91 Hz)

3 实例分析

某分离式立交大桥(图1)，该桥为桥梁纵向按平坡设计，横向坡度均为2%。一联为2×40 m的装配式预应力混凝土连续箱梁。采用多箱单独预制，简支安装，现浇连续接头的先简支后连续的结构体系。为了便于模板制作和外形美观，主梁沿纵向外轮廓尺寸保持不变，设计荷载等级为公路－Ⅰ级。

采用一辆重为38.1 t的载重汽车，测点布置见图2、图3。在桥面无任何障碍的情况下，分别以40 km/h、50 km/h速度驶过桥跨结构，根据控制截面测点在行车试验时记录的动挠度曲线进行分析处理计算活载冲击系数。

根据结构动力学的基本原理，当荷载频率与结构的自振频率相等或接近时，体系将发生共振，共振引起很大的动力响应。为了研究采用最小二乘法拟合曲线的有效性，因此对不同跑车速度下桥梁动力响应曲线进行分析。

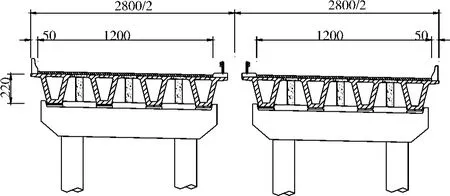
图1 桥梁剖面

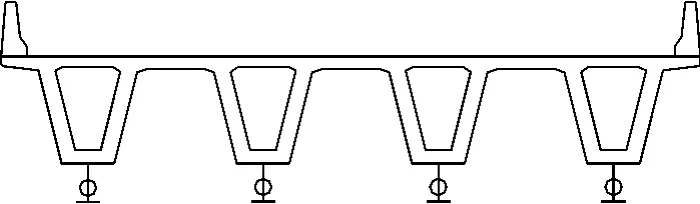
图2 挠度测点布置

图3 应变测点布置

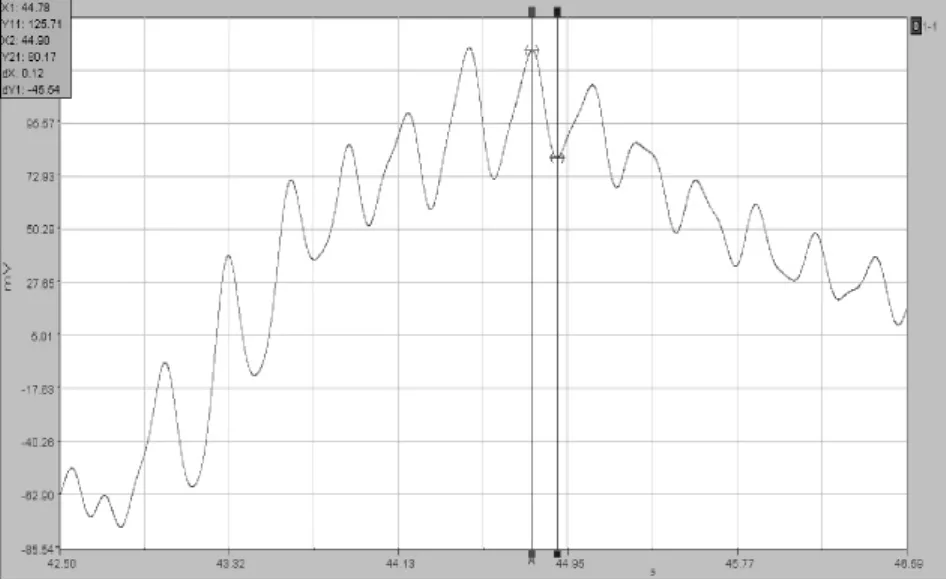
图4 40 km/h跑车时程曲线

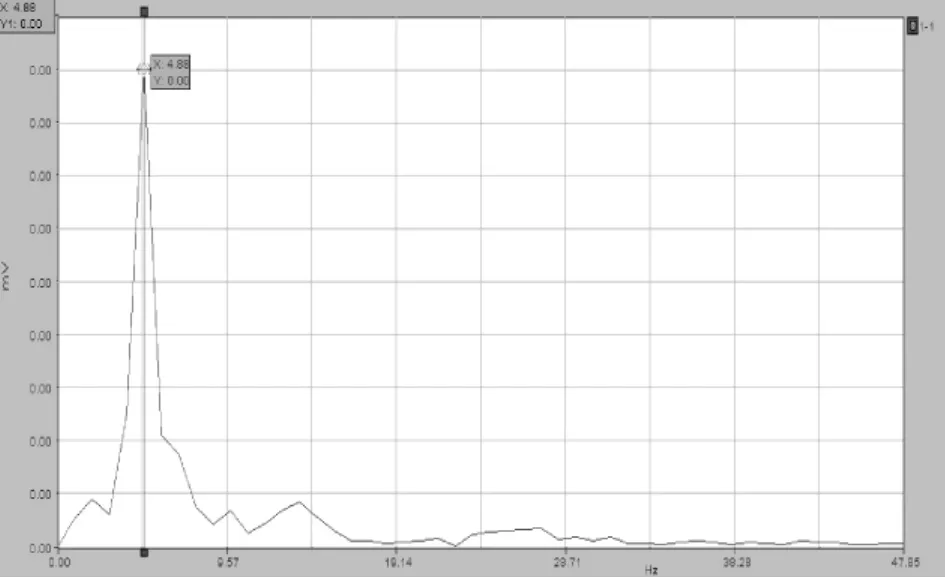
图5 40 km/h跑车频谱分析

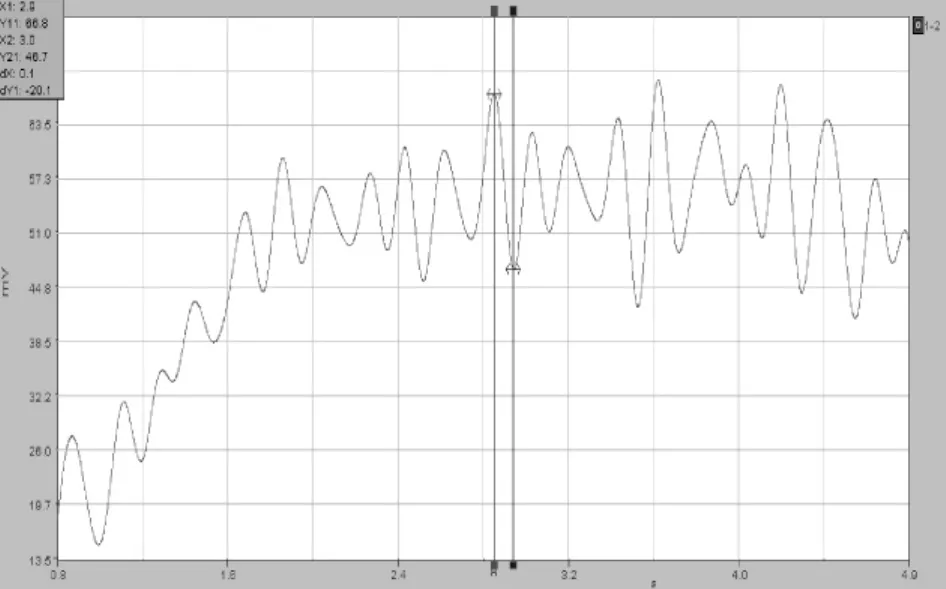
图6 50 km/h跑车时程曲线

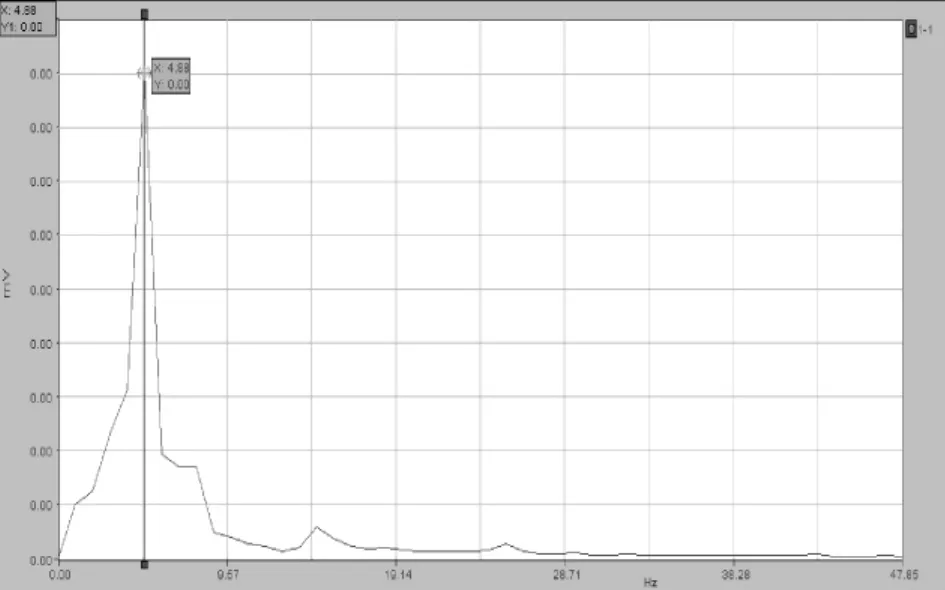
图7 50 km/h跑车频谱分析

图4～图7为最不利位置下冲击系数随车辆速度变化图，从图中可以看出，光滑路面下，车辆自振频率和跑车速度变化区别不大。

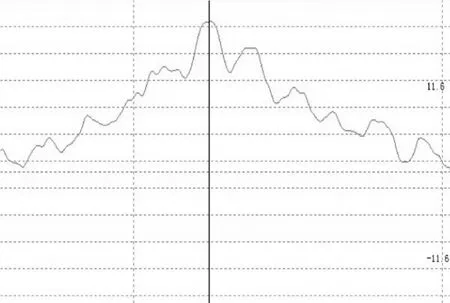
图8 移动最小二乘拟合40 km/h值

图8为采用matlab编写计算程序将实验仪器测出值进行分析得到图形。有图中可见经过移动最小二乘拟合图形较为光滑，有着更好的连续性。

?

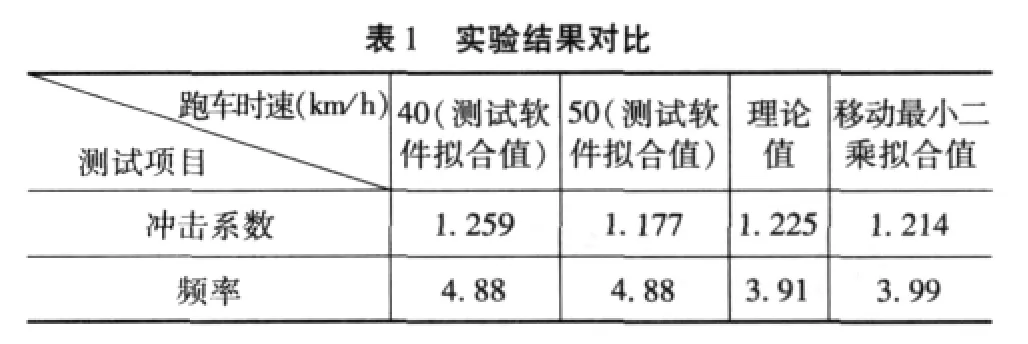
上表为将常规算法结果、理论计算结果与采用移动最小二乘拟合得到的结果进行对比，由计算结果可看出采用移动最小二乘拟合得到的值较常规方法计算出的值更为接近理论结果。

4 结论

通过理论计算同实际实验结果 进行比较，可知由于移动最小二乘法进行实验数据分析时，往往能得到可导阶次更高的曲线，因此能够更好的反映实际桥梁工作时候的“连续”特性，并又能很好的“体现冲击系数”的局部特性。不会只强调数据拟合时需要曲线更为连续而丢失其局部特征。能够更好地体现桥梁工作特性。

［1］T Belytschko，Y Krongauz，D Organ，M Fleming，P Krysl.Meshless methods:an overview and recent developments［J］.Computer Methods in Applied Mechanics and Engineering，1996，139:3 －48

［2］秦荣，谢肖礼.结构弹塑性分析的新方法［J］.广西大学学报(自然科学版)，1994(3)

［3］周小平，周瑞忠.无单元法研究现状及展望［J］.工程力学，2005，22(1):12 －20

［4］李秀梅，秦荣，王建军.样条无单元法在弹性薄板振动问题中的应用［J］.广西大学学报(自然科学版)，2007(1)

［5］李秀梅，秦荣，谢开仲.弹性地基板分析的样条无单元法及其C程序设计［J］.广西大学学报(自然科学版)，2004(3)

［6］张雄，宋康祖，陆明万.无网格法研究进展及其应用［J］.计算力学学报，2003(6)

［7］李双蓓，刘立国，倪骁慧.结构稳定性研究的现状和新方法的探索［J］.广西大学学报(自然科学版)，2004(2)

［8］龙建旭，石东艳.配点型无网格法的误差影响因素分析［J］.广西大学学报(自然科学版)，2009(2)