一种高超声速飞行器的再入约束非线性控制方法*

张 军，王 玫

(1.江苏大学电气信息工程学院，江苏 212013;2.上海机电工程研究所，上海，200233)

近空间无动力滑翔返回的高超声速飞行器再入段采用传统PID增益调度控制很难适应大包络、多任务模式飞行运动［1］.高超声速飞行器控制系统存在快时变、强非线性耦合、不确定性、多干扰、高实时性等特性.因此，非线性控制和鲁棒控制应用到控制器设计中，成为国内外理论和工程界研究热点.

由于再入走廊的防热和力学安全边界要求，高超声速飞行器控制系统必须满足严格的输入约束，包括力矩、舵机的偏角、带宽等;以及状态约束，包括角度、角速度等.动态逆控制、变结构控制［2］、神经网络控制［3］、自适应后退法鲁棒性强［4］，但是容易造成输入超限，没有系统地解决多约束问题，即使处理也是事后处理，影响高机动性的控制性能.基于反馈校正和滚动优化策略的预测控制是解决约束的有效方法之一，文献［5］将反馈线性化和线性预测控制结合起来解决高超声速飞行器的输入约束，虽然通过非线性变换把非线性预测模型转化为线性模型，但是控制约束转化成非线性的，处理仍然比较复杂.文献［6］将非线性动力学伪线性化，基于线性矩阵不等式优化解决输入约束，计算量较大.文献［7-8］将连续非线性时变预测控制应用到高超声速飞行器的上升段和再入段制导中，执行效率高，避免了复杂的数值计算，本文将该方法应用到高超声速飞行器的姿态控制中.

为减少设计复杂性，基于奇异摄动理论提出了内外环解耦控制系统.控制系统的外环姿态运动耦合较弱，在满足角速度约束的条件下采用非线性时变预测控制实现角度跟踪，并提出改进的一步滑模预测控制抑制大干扰.强耦合的内环采用动态逆跟踪外环角速度指令，动态逆期望动力学采用PI形式提高内环的鲁棒性，基于变结构抗饱和技术调整控制参数处理输入饱和约束.最后，通过仿真验证了算法的有效性.

1 模型描述

具有面对称外形的高超声速飞行器的再入无动力模型为:

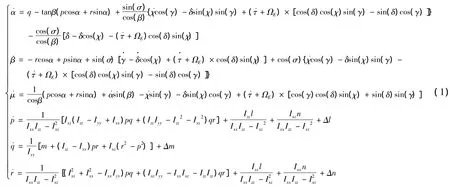
式中，α，β，μ分别是飞行器的攻角、侧滑角、倾斜角;χ是方位角，δ为纬度，τ为经度，ΩE为地球自转角速率;p，q，r分别是飞行器的滚动角速度、俯仰角速度、偏航角速度;Ixx，Iyy，Izz分别是飞行器的主转动惯量，由于飞行器相对于x-z平面对称，Ixz≠0.l，m，n分别是飞行器的滚动力矩，俯仰力矩和偏航力矩，由RCS(反作用控制系统，reaction control system)和气动舵面联合控制.Δl，Δm，Δn为气动力矩参数、惯量不确定性、结构干扰等带来的组合干扰，具体的形式参见文献［9］，这里省略.从式(1)可以看出，高超声速飞行器姿态动力学模型是时变的非线性系统，并且与轨道参数耦合［1-4］.

2 控制器设计

由于状态变量的动态响应过程具有明显时间尺度差异的特性，因此根据奇异摄动理论，采用分阶控制的思想，将状态变量分为两个层次:其中攻角α、侧滑角β和倾斜角μ为慢变量，频带在1～2rad/s;滚转角速度p、俯仰角速度q和偏航角速度r为快变量，频带在 5 ～10rad/s［10］;控制舵面或者 RCS 对于［α，β，μ］的作用是非常慢的，对于［p，q，r］的作用比较快.因此，在设计［p，q，r］的控制律时，可近似认为［α，β，μ］变量为常量;设计［α，β，μ］的控制律，不考虑［p，q，r］的动态响应过程.外环的输出期望p，q，r作为内环的输入跟踪命令(见图1).基于奇异摄动理论的动态逆方法是X-38成功返回应用的技术［11］，该方法综合的系统无需复杂的变增益调节，能够以固定增益自动适应飞行条件和构型的大范围变化，但是要求模型精确，鲁棒性较差，不能处理输入和状态约束.本节采用预测控制来解决鲁棒性和约束问题.

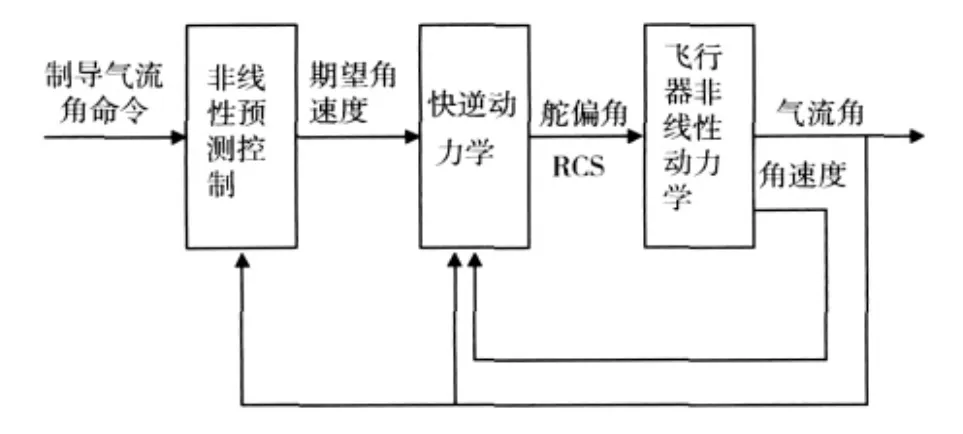
图1 控制系统结构

2.1 外环设计

将外环的姿态运动学方程写为下面的设计模型形式:

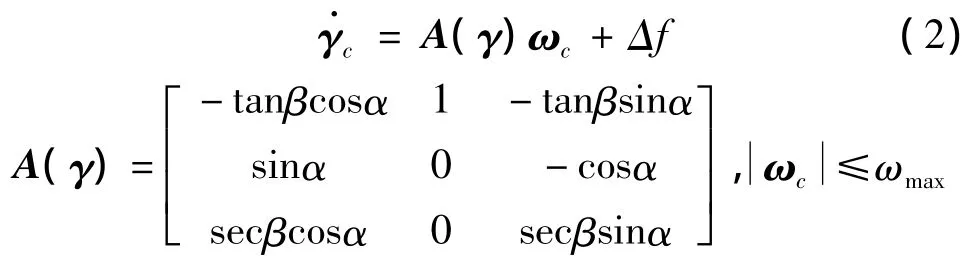
其中 γc= ［αc，βc，μc］T，ωc= ［pc，qc，rc］T，Δf为姿态运动方程中的轨道运动对姿态运动的时变耦合量，由于地球自转角速率ΩE以及轨道运动比姿态运动慢很多，因此Δf为时变的不确定小量，影响期望角速率的主要是=A(γ)ωc.由于再入过程中是大攻角往往大于10°)，因此姿态运动方程是三通道耦合，不能利用小攻角系数冻结法线性化.文献［12］给出外环的PI(比例积分)设计形式(2)，进行飞行包络内的控制可靠性分析，这意味传统的设计使控制系统具有一定的幅值裕度和相位裕度能抑止有界的耦合和干扰的影响，sat是饱和函数，但是这需要一定的经验值.

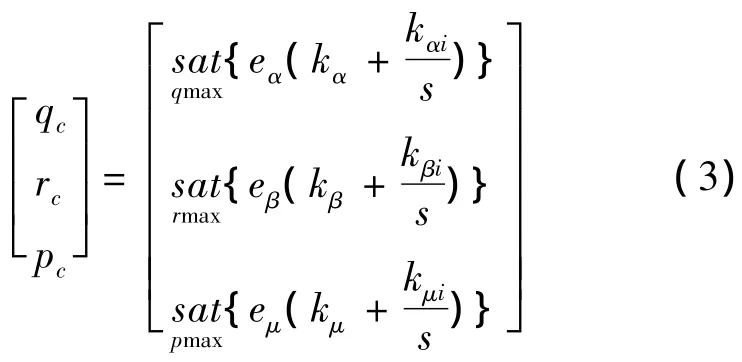
饱和函数定义:

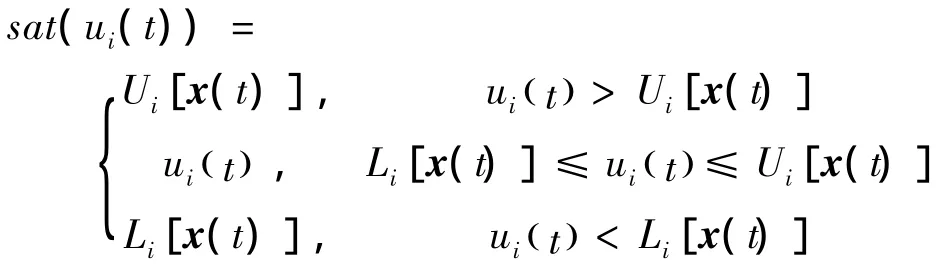
对于控制系统来说，外环控制的目的是气流系角无静差跟踪制导指令.预测控制是解决约束的有效控制方法之一，并且鲁棒性好，可通过在线反馈以抑制模型Δf的变化.有约束非线性系统的预测控制没有解析解，一般采用非线性规划数值求解;由于高超声速飞行器的实时性要求，这里采用计算时间最少的近似非线性连续的预测控制实现角度的跟踪［7］，在控制性能和实时性之间进行折中，提出基于一步误差和一步滑模预测两种方法.

(1)为了便于求解一步预测的近似连续控制律，将姿态运动学方程另写成下面的形式:

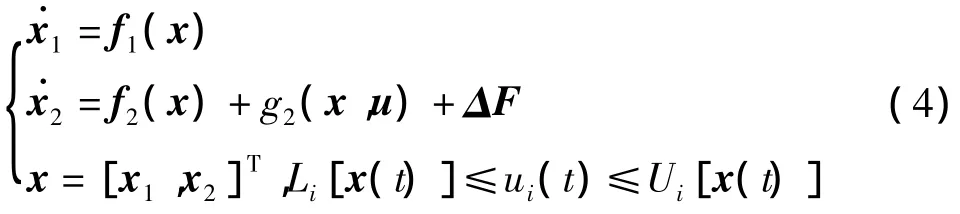
基于标称模型的一步预测误差近似为:

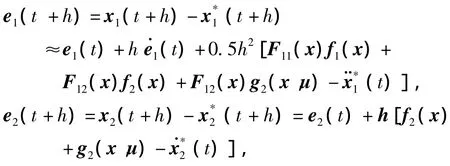
式中 F11= ∂f1［x(t)］/∂x1，F12= ∂f1［x(t)］/∂x2，为期望的状态.为减少计算量预测时域选为1，预测优化性能目标为:

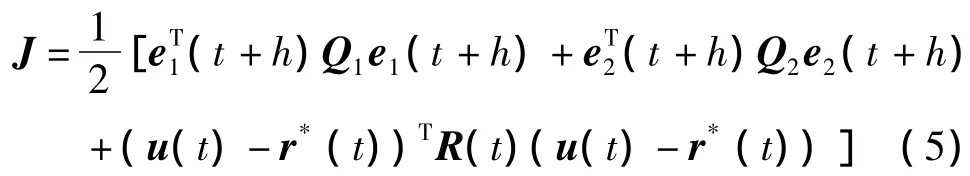
式中Q1，Q2，R分别为跟踪误差和控制量的加权项，e(t+h)是基于t时刻在t+h时刻的误差预测值，u(t)是当前时刻的输入，r*(t)是期望前馈输入.由最优化的必要条件得到控制量为:

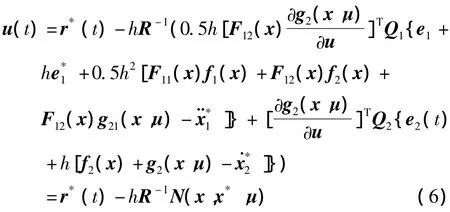
应用饱和函数处理输入约束得到:

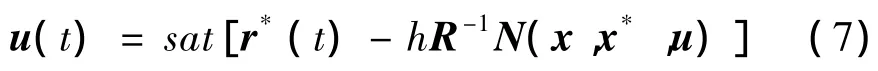
对于姿态运动学方程式(4)f1(x)，f2(x)为零，x1=0，x2=［α β μ］T，式(6)等价为:

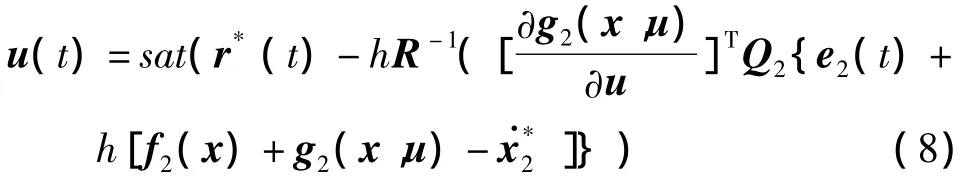
当式(2)时变耦合量Δf幅值较小且变化较慢时，可通过预测控制的在线反馈策略得到有效抑制［7］.当Δf较大时，基于标称模型预测的控制量式(7)有明显的跟踪误差，需要强鲁棒性的预测控制，这里通过引入增广积分变量来抑制干扰造成的跟踪误差.

定义误差γe=γc-γ，选择式(2)的滑模为:

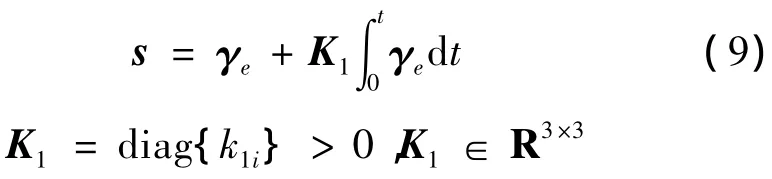
基于一步滑模预测的优化目标为:

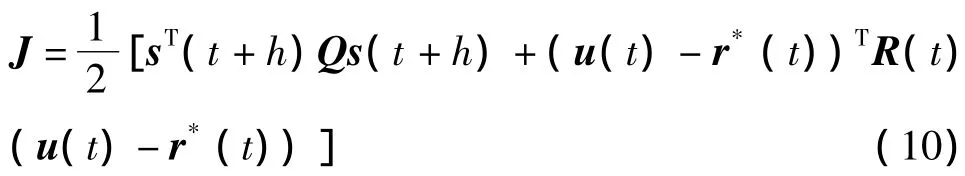
基于滑模预测的终端约束集sTQs≤1比状态预测的终端约束集xTQx≤1大，减小了预测时域和计算量［13］.同时，具有了滑动平面上滑动模态对干扰不变性的优点，优化了预测性能.

对滑模函数进行微分得到:

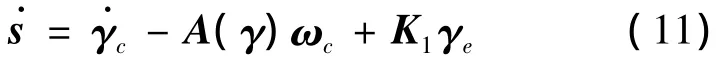
滑模的一步预测误差为:

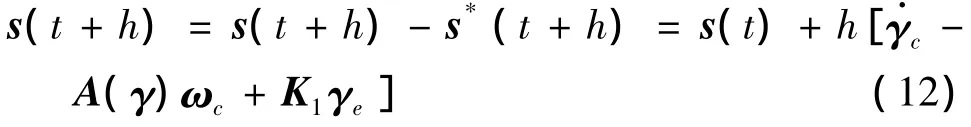
s(t+h)是基于t时刻在t+h时刻的滑模预测值，u(t)是当前时刻的输入，r*(t)是期望前馈输入.由最优化的必要条件，得到控制量为:

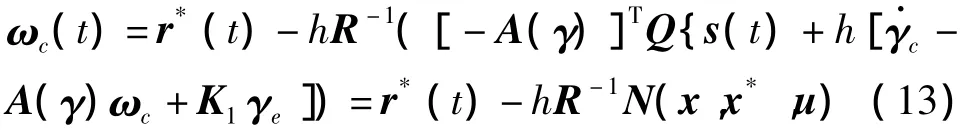
应用饱和函数处理输入约束得到

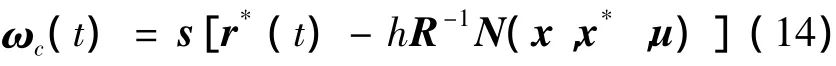
注释.预测步长h，加权矩阵Q，R与输入量大小和跟踪精度有关，选择需要注意［7］.基于滑模预测的优化控制律(13)是连续的控制律，不是滑模控制，不具有滑模控制的抖振和切换特点.

2.2 内环设计

pc，qc，rc作为内环的跟踪输入命令，从动力学模型(1)的后三个力矩与角速度关系知道，非对称体飞行器存在力矩和运动的强耦合，并且动力学模型随着飞行马赫数和动压快速变化，即Cl，Cm，Cn随着飞行马赫数和状态急剧变化，导致姿态动力学是快速时变的，需要大量地面人工计算，实现增益调度.内环采用式(7)或者式(13)求取力矩或者舵机偏角，但由于内环是快变量响应，实时性高，因此内环采用动态逆跟踪角速度指令［2］，无需复杂的变增益调节，能够以固定增益(反映带宽)自动适应飞行条件和构型的大范围变化.将姿态动力学方程中的动力学模型不确定(气动力矩参数，惯量)、不同的组合干扰力矩(结构干扰)合并为［Δl，Δm，Δn］T，得到:

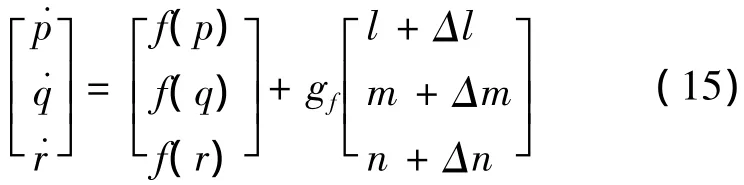
利用动态逆得到期望虚拟输入:

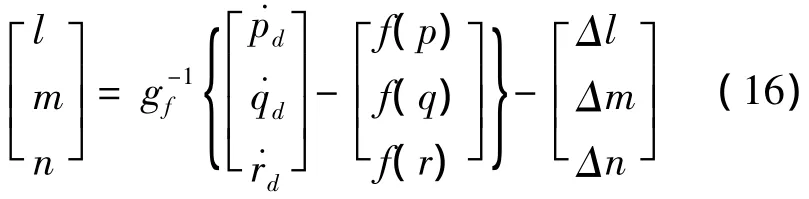
式(15)是内环跟踪期望角速度的需要总力矩，由RCS和气动舵面联合分配控制，根据不同的执行结构gf有不同的形式，具体的力矩分配方式不作讨论，见文献［10］.文献［14］通过低阶滑模观测器估计干扰力矩［Δl，Δm，Δn］T，直接进行前馈补偿，估计参数较多;一般文献选取比例形式，但是难以消除干扰力矩影响，这里选择期望特性为PI(比例积分)形式，抑制补偿干扰和不确定性的影响，以及逆计算的误差，期望形式如下:

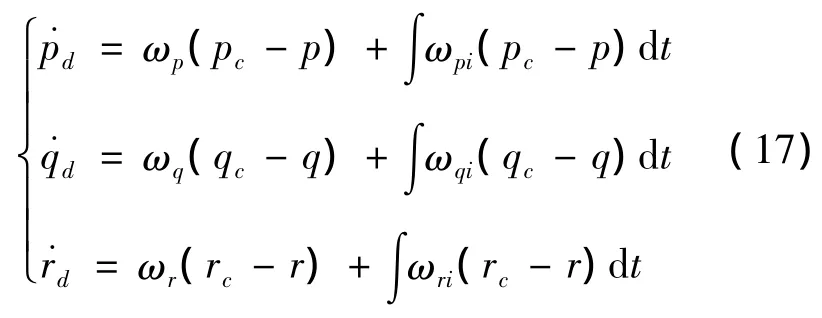
PI参数选择与内环的带宽相关，是时变的.由于实际力矩和舵机偏角往往有幅值约束，即或者，而动态逆PI期望闭环形式在角速度误差较大时，很容易造成饱和现象.为了既可以利用传统的PID理论设计期望控制器，又可以尽快使控制器退出饱和区，选择变结构Anti-Windup控制器.实现简单、鲁棒性好，适合于工程应用［15］.积分控制量调整为下面的形式:

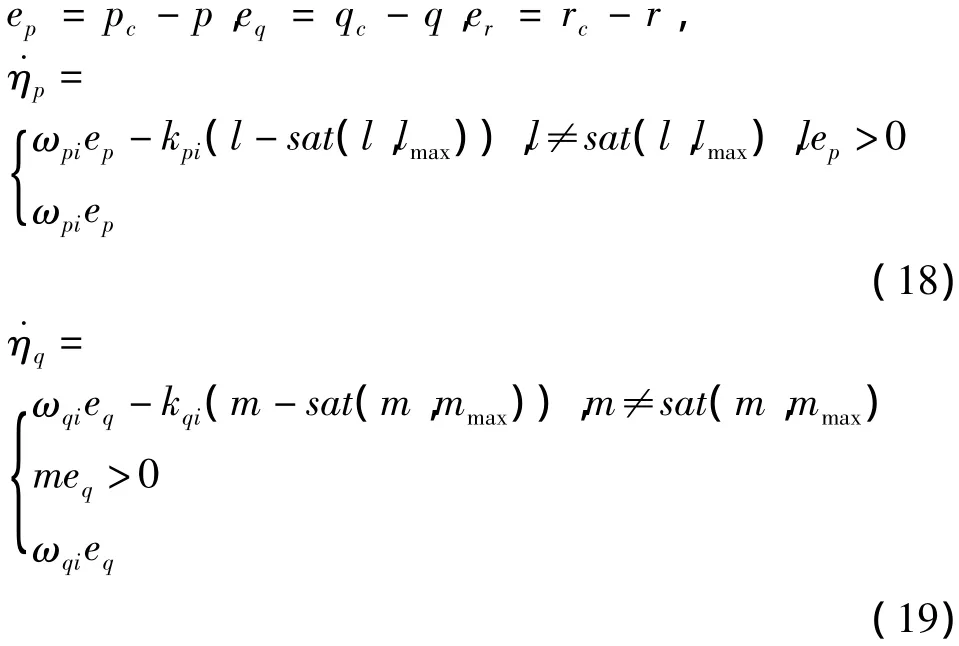
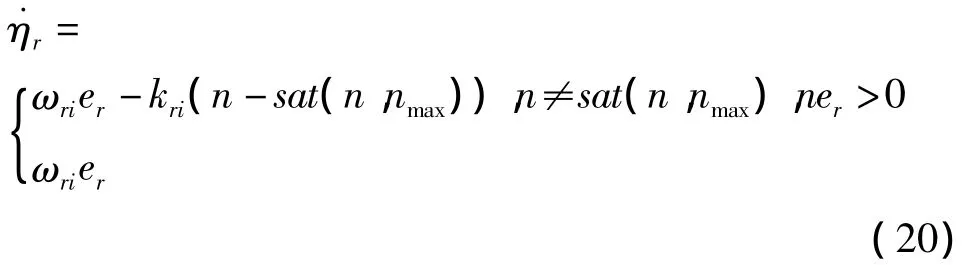
式中 kpi，kqi，kri是补偿系数.

3 仿真研究

飞行器模型和气动参数来自NASA的报告［16］，飞行器质量为63503kg，机翼参考面积334.73 m2.飞行器的V=3000m/s，γ =-3°.仿真条件初值:α =15°，β =3°，μ =5°期望值:α =12°，β =0°，μ=0°(滑翔无动力再入飞行器的攻角是大攻角，与巡航飞行不同).仿真周期20ms.α，β，μ三通道姿态运动分别加上惯量变化10%，常值力矩干扰为100000N·m.力矩最大约束值4×106N·m，角速度最大约束值100(°)/s(这里约束不是真实的数据，主要验证算法有效性).分两种情况仿真研究:

1)当 Δf=0.1sin(0.01t)［111］T时，图2～4是采用一步误差预测控制的角度、角速度、力矩仿真曲线，力矩和角速度满足约束要求，近似的连续预测控制具有一定干扰的能力.

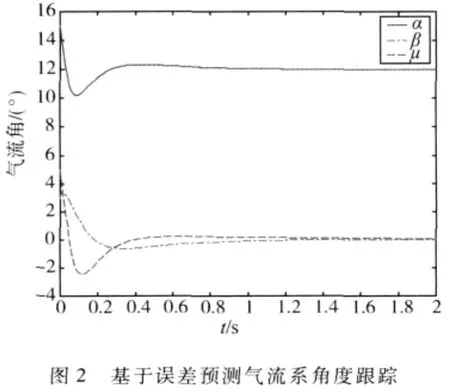
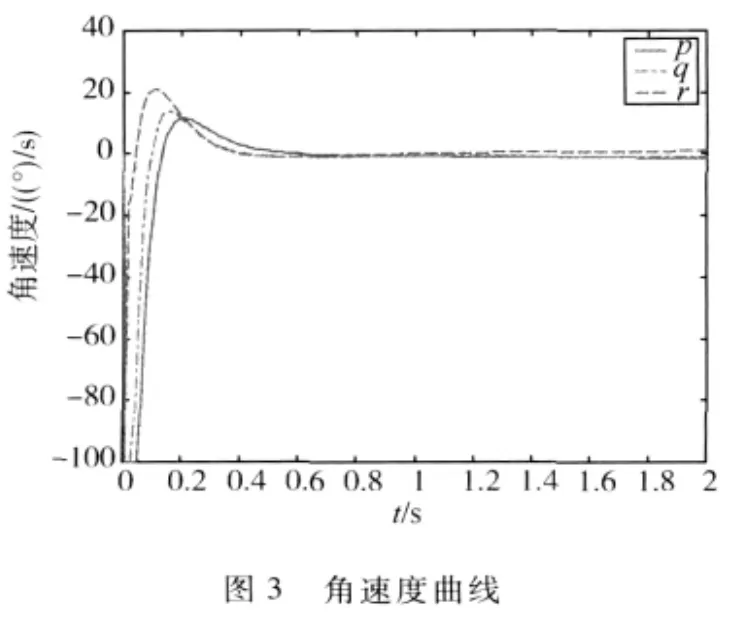
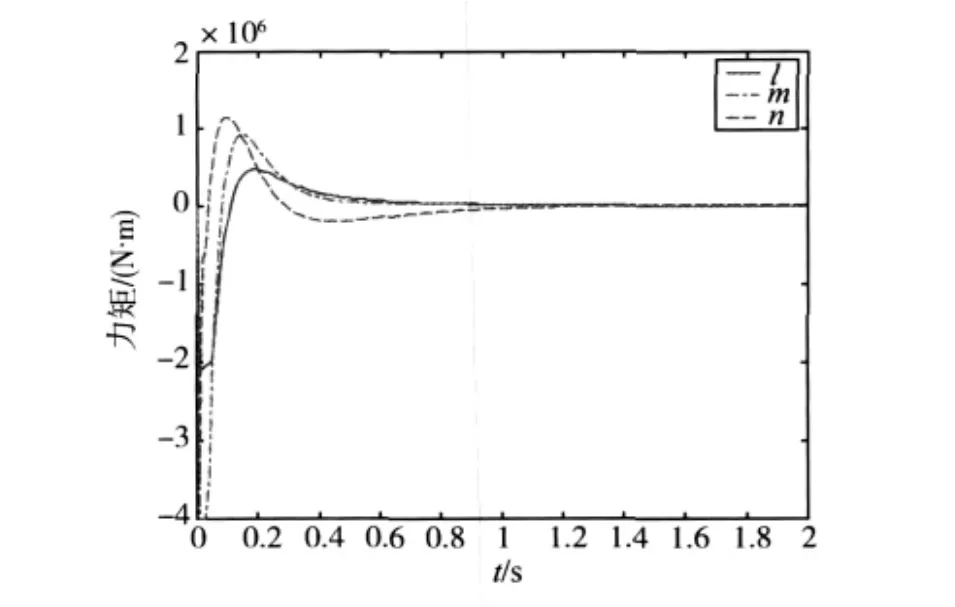
图4 力矩曲线

2)当 Δf=0.5sin(0.1t)［111］T时，采用式(7)有明显的稳态误差(图6);采用式(13)滑模预测控制量有较高的稳态性能(图5)，具有抑制大干扰的能力.

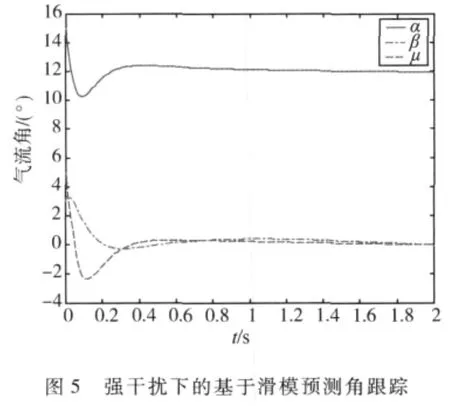
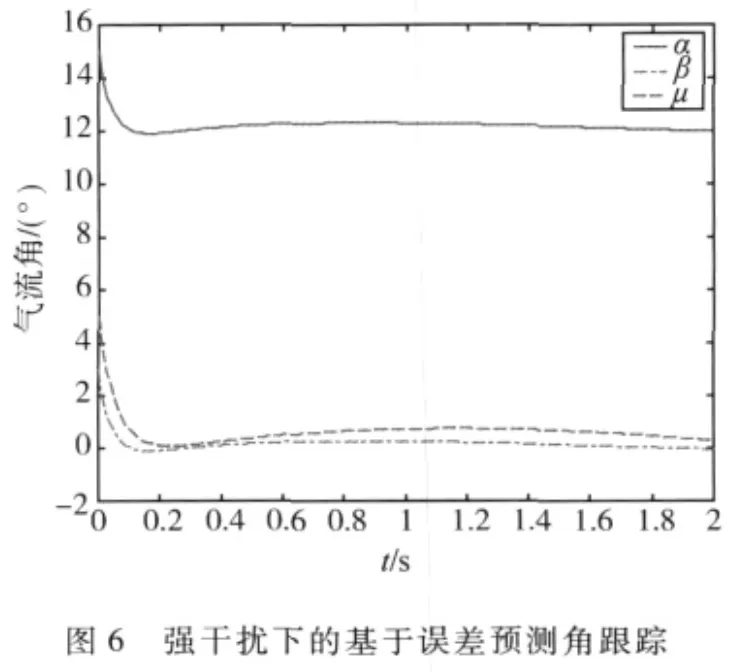
4 结论

针对高超声速飞行器非线性动力学模型，基于奇异摄动理论提出了内外环解耦控制系统.控制系统的外环姿态运动耦合较弱，在满足角速度约束的条件下设计高效率的非线性时变预测控制和滑模预测控制跟踪角度指令，控制律形式简单.强耦合的内环采用动态逆跟踪外环角速度指令，动态逆期望动力学采用PI形式提高内环的鲁棒性，基于变结构抗饱和技术处理执行结构的饱和约束.最后，通过仿真验证了算法的有效性.

［1］ Harpold J.Shuttle entry guidance［J］.Journal of the Astronautical Sciences，1979，28(3):239-268

［2］ Yuri B S，Charles E H.Reusable launch vehicle control in multiple-time scale sliding modes［J］.Journal of Guidance，Control and Dynamics，2000，23(6):1013-1020

［3］ 敬忠良，朱亮，陆平.基于轨迹线性化方法的近空间飞行器鲁棒自适应控制［J］.空间控制技术与应用，2008，34(1):38-43

［4］ 高道祥，孙增祈.高超声速飞行器离散模糊自适应控制［J］.空间控制技术与应用，2009，35(5):13-19

［5］ Van WR.Combined feedback linearization and constrained model predictive control for entry flight［J］.Journal of Guidance，Control and Dynamics ，2006 ，29(2):427-434

［6］ 邵晓巍，张军，牛云涛.高超飞行器的非线性预测姿态控制［J］.弹道学报，2009，(4):42-46

［7］ Lu P.Optimal predictive control of nonlinear systems［J］.International Journal of Control ，1995，62(3):633-549

［8］ Brinda V，Dasgupta S.Guidance law for an air-breathing launch vehicle using predicitve control concept［J］.Journal of Guiance Control and Dynamics，2006，29(6):1460-1463

［9］ 杨俊春，胡军，吕孝乐.高超声速飞行器再入段模跟踪控制设计［C］.第26届中国控制会议，张家界，2007

［10］ Ito D.Robust dynamic inversion controller design and analysis(using the X-38 vehicle as a case study)［D］.Houston:Department of Aerospace Engineering，Texas A＆M University，2001

［11］ Ert S U，Görlach T，Roenneke A.German contribution to the X-38 CRV demonstrator in the field of guidance，navigation and control［J］.Acta Astronautica，2004，56(8):737-749

［12］ Juliana S，Chu Q P，Mulder A.Reentry flight clearance using interval analysis［J］.Journal of Guidance，Control，and Dynamics，2008，31(5):1295-1307

［13］ Zhou JS，Liu ZY，Pei R .A New nonlinear model predictive control scheme for discrete-time system based on sliding mode control［C］.American Control Conference.Arlington，USA，June，2001，3079-3084

［14］ Charles E H，Yuri B S.Sliding mode disturbance observer-based control for a reusable launch vehicle［J］.Journal of Guidance，Control and Dynamics，2006，29(6):1315-1328

［15］ Hodel A S，Hall C E.Variable-structure PID control to prevent integrator windup［J］.IEEE Transactions on Industrial Electronics，2001，48(2):442-451

［16］ Shahriar K.Six-DOF Modeling and simulation of a generic hypersonic vehicle for conceptual design studies［C］.Modeling and Simulation Conference，Chicago.USA AIAA，2004