基坑降水对周边建筑物影响浅谈
付 丽 李晶岩
1 概述
进入21世纪,我国的城市建设发展迅速,城市的规模以及人口都有了巨大的增长。同时作为城市化的产物之一高层建筑不仅在数量上越来越多,而且在高度上也越来越高,基坑的面积和深度也向大而深的方向发展,而在地下水位高的地区,工人需要干燥的工作环境,其施工过程中必须降水。
有效降水可以给施工人员提供干燥工作面,避免水下作业,使基坑施工能在水位以上进行,为施工人员提供操作可能性,也有利于提高施工质量。消除及减少作用在边坡或坑壁围护结构上的静水压力与渗透压力,提高边坡或围护结构的稳定性。防止地下水因渗流而产生流砂、管涌等破坏作用。
但降水也有不利作用,对邻近环境有不良影响,主要是随着地下水位的降低,在水位下降的漏斗范围内,土体的自重将增大,这样在降水水位影响范围的地面,包括建(构)筑物就会产生附加沉降,该附加沉降在上部结构中再次产生附加应力增量,该结构内力大于结构的抗力时,上部结构发生开裂,对邻近环境总是会有或大或小的影响,如果不认真对待,就会造成严重的后果。
本文以实际深基坑降水工程为依托,研究邻近基坑降水引起的地面沉降对建筑物的影响。
2 降水引起沉降机理方程建立
测压管水头为:

其中,z为某点相对于任意选定的基准面的高度,称为位置水头,m;p为某点的水压力,在土力学中称为孔隙水压力,Pa;γw为水的容重,N/m3;为某点孔隙水压力的水柱高度,称为压力水头,m;总水头为测压水头和流速水头之和,即:

其中,vw为某点处的渗流速度,m/s;为流速水头,m。
由于土中渗流阻力较大,地下水的运动很缓慢,流速水头很小,可以忽略不计。因此在渗流计算中,可以认为总水头h等于测压管水头hn,即:

根据有效应力原理,某点处竖向有效应力σ'应为:

渗流的连续性方程:

渗流基本微分方程:

3 模型建立
地质条件:根据勘察设计院提供的地质资料,勘察期间场区地下水位:初见水位为-6.6 m~-7.2 m,静止水位为-6.6 m~-7.2 m,其稳定水位基本判定在-6.6 m,考虑到水位上涨等因素,地下静止水位按-6.0 m作为本工程的静止水位。拟建工程基底埋深9.0 m(自然地面起算),为保证在基础开挖及基础施工过程中正常施工,并考虑降水液面与基础最低点的安全距离为0.5 m,故其地下水位必须降至-9.5 m(自然地面起算)以下。
①杂填土:含碎石、灰渣、砂土建筑垃圾和生活垃圾,层底埋深2.0 m~3.6 m。②粉质粘土:黄褐色,饱和、流塑,中~高压缩性,层底埋深5.6m~6.8m,层厚3.5m~4.6m。③粘土、粉质粘土:黑褐色~黄褐色,可塑,中压缩性,层底埋深2.5 m~7.4 m。④粉质粘土:灰褐色,软塑,流塑,中~高压缩性,层底埋深4.7 m~8.2 m。⑤粉砂:黄色~灰色,可塑,稍密,湿~饱和,层底埋深7.0 m~14.0 m。⑥细砂:黄色~灰色,可塑,稍密,饱和,层底埋深12.2 m~16.8 m。厚度6.0 m~9.2 m。⑦中砂:黄色~灰色,可塑,稍密~中密,饱和,层底埋深16.7 m~20.1 m。最大厚度7.0 m。⑧粉质粘土:灰色,可塑,中压缩性,层底埋深18.2 m。⑨粉质粘土:灰色,可塑,中压缩性,层底埋深19.0 m~24.6 m。
本模型使用六面体单元,单元数量为153 600个。
初始条件:计算模型的应力初始条件由自重应力生成,计算模型的渗流初始条件为定水头,初始潜水位在地表以下6 m处。
边界条件:左右边界作为定水头边界(补给边界),左右计算边界为基坑深度的3倍(20 m),在基坑壁处有止水帷幕,所以降水对左右计算边界的水位影响很小。下边界作为流量为零边界,下边界取基坑深度的5倍(32 m),降水对此边界影响很小。
4 计算结果
图1为建筑物角点的竖向位移随井点至建筑物角点的距离改变的变化规律。由图1可见,在井点至建筑物角点的距离为29 m~39.5m时,曲线的斜率很缓,位移随井点至建筑物角点距离变化很小,位移增大趋势不明显;在井点至建筑物角点的距离为17m~29 m时,曲线斜率开始变陡,建筑物角点位移随井点至建筑物角点距离变化增大,位移增大趋势明显。图2是在井深发生变化的情况下,建筑物角点的竖向位移随其变化的规律。由图2得出,在井深为12 m~15m时,曲线斜率很缓,位移随井深变化很小,位移增大趋势不明显;在井深为15 m~24 m时,曲线斜率开始变陡,位移随井深增大开始增大,位移增大趋势较明显。
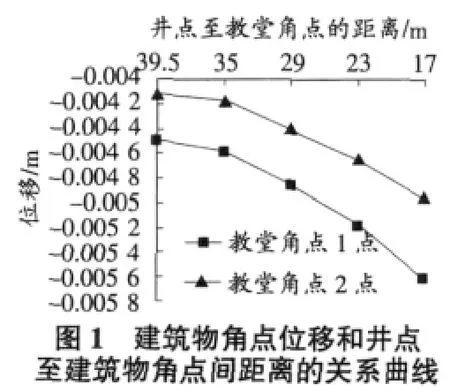
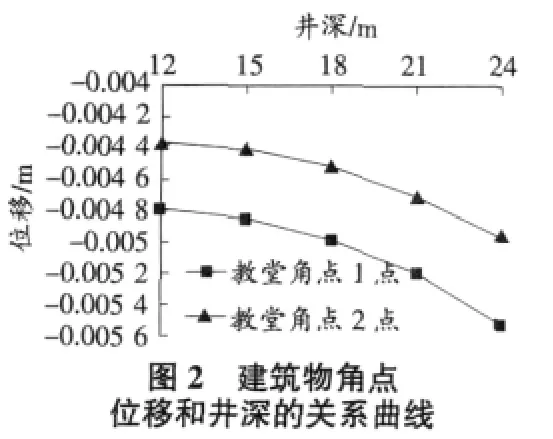
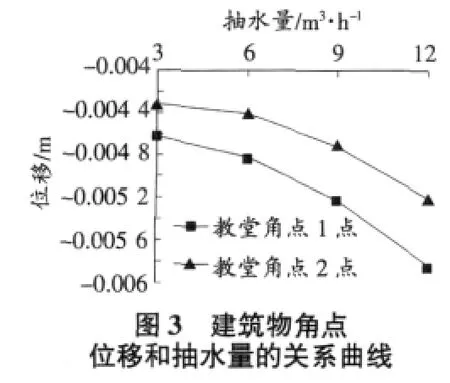
图3为建筑物角点的竖向位移随抽水量改变的变化规律。由图3得出,在抽水量为3 m3/h~6 m3/h时,曲线的斜率很缓,位移随抽水量变化很小,位移增大趋势不明显;在抽水量为6 m3/h~12 m3/h时,曲线斜率开始变陡,建筑物角点位移随抽水量增大开始增大,位移增大趋势明显;在抽水量为3 m3/h~6 m3/h时,曲线的斜率很缓,水位随抽水量变化很小,水位减小趋势不明显;在抽水量为6 m3/h~12 m3/h时,曲线斜率开始变陡,水位随抽水量增大开始减小,水位减小趋势明显。
图4为建筑物角点的竖向位移随渗透系数改变的变化规律。由图4得出,在渗透系数为3m/d~6m/d时,曲线的斜率很缓,位移随渗透系数变化很小,位移增大趋势不明显;在渗透系数为6 m/d~12 m/d时,曲线斜率开始变陡,建筑物角点位移随渗透系数增大开始增大,位移增大趋势明显。在渗透系数为3 m/d~6 m/d时,曲线的斜率很缓,水位随渗透系数变化很小,水位减小趋势不明显;在渗透系数为6 m/d~12 m/d时,曲线斜率开始变陡,水位随渗透系数增大开始减小,水位减小趋势明显。

5 结语
本文通过对实际工况条件下的计算,得到建筑物角点处竖向位移的变化规律。
1)随着井群距离建筑物角点越来越近,井群对建筑物角点处的降水作用越来越强,建筑物角点处土中地下水位降低较大,地面沉降增加较大。
2)随着井点深度越来越大,渗流路径长度不断减小,井点对建筑物角点处的降水作用越来越强,使建筑物角点处土中地下水位降低越来越大,地面沉降增大。
3)随着单井抽水量的逐渐增大,外界机械能量逐渐增大,井点对建筑物角点处的降水作用增强,建筑物角点处水位降低,地面沉降增大。
4)随着止水帷幕深度的增大,渗流路径长度越来越大,井点对建筑物角点处的降水作用减弱,建筑物角点处土中地下水位降低越来越小,地面沉降逐渐减小。
5)本工程采用井深15 m,单井抽水量6 m3/h,止水帷幕16 m,进行降水工程是合理的。
6)工程中使用回灌和止水帷幕两种技术措施有效地减小了沉降变形速率。最终邻近基坑降水引起的地面沉降仅为0.004 m,对建筑物上部结构没有影响。
[1] 胡其志,何世秀.基坑降水引起地面沉降的分析[J].湖北工学院学报,2001,16(1):66-69.
[2] S.S.Kishnani,R.I.Borja.Seepage and soil-structure interaction in braced excavations[J].Journal of Geotechnical Engineering,ASCE,1993,19(5):912-928.
[3] 顾慰慈.渗流计算原理及应用[M].北京:中国建材工业出版社,2000:2-16.
[4] A.Leontiev,W.Huacasi.Mathematical programming approach for unconfined seepage flow problem[J].Engineering analysis with boundary elements,2001(25):49-56.
[5] Nunzio Romano,Bruno Brunone,Alessandro Santini.Numerical analysis of one-dimension unsaturated flow in layered soils[J]. Advances in Water Resources,1998(21):315-324.
[6] 王 滨,贺可强.阶梯流量法在深基坑降水中的应用[J].施工技术,2002,31(1):23-25.
[7] 王翠英,殷坤龙,王家阳.建筑工程基坑降水设计方案优化的探讨[J].施工技术,2005,34(1):15-17.
[8] 胡 静.复合单元法在深基坑降水井设计中的应用[J].水力发电,2005,31(2):41-43.
[9] 张立杰,秦紫东,东迎欣,等.基坑降水的三维非稳定渗流数值模拟[J].低温建筑技术,2005(4):79-80.
[10] 庞景兰.基坑开挖工程中渗流场的三维有限元分析[J].水科学与工程技术,2006(6):24-26.
[11] 纪佑军,刘建军,薛 强.基坑地下水渗流数值模拟[J].武汉工业学院学报,2006,25(1):72-77.
[12] 谢康和,柳崇敏,应宏伟,等.成层土中基坑开挖降水引起的地表沉降分析[J].浙江大学学报,2003,36(3):239-242.
[13] 何世秀,胡其志,庄心善.渗流对基坑周边沉降的影响[J].岩石力学与工程学报,2003,22(9):1551-1554.

