适用于宽温度和压力范围的湿空气热力性质分段计算方法

袁 智, 陈坚红, 盛德仁, 李 蔚, 杨 扬, 周晓宇

(1.浙江大学 能源工程学系,杭州 310027;2.杭州华电半山发电有限公司,杭州 310015)

热力循环工质的热物理性质数据是工程热物理学科领域中进行科学研究、工程设计等工作的基础,随着实际应用的需要,对其的研究也不断深入和发展,对于湿空气这种工质的研究也是如此.1983年,由日本学者M ori首先提出的湿空气透平循环(HAT)具有造价低、效率高及污染物排放少等优点,在其关键部件——饱和器中,高温喷雾水滴(或填料上的水膜)与高压压缩空气接触,部分吸热蒸发,形成高温、高含湿量的饱和湿空气,其出口温度可达523.15 K,压力高于 5 MPa[1-3].在 HAT循环过程中,饱和器的主要作用是增加工质流量,从而增大比功、降低水温以及回收系统的余热.因此,分析饱和器的性能十分重要,但其前提是要对湿空气的热力性质进行准确计算.在上世纪50年代提出的压缩空气储能[4](CAES)是一种新型高效储能技术,CAES系统在电力供应中起着削峰填谷的作用,其工质(湿空气)的压力要求达到20 MPa.

目前,湿空气的热物理性质计算模型有三类:理想模型、经验模型和半经验模型.通常,理想模型把湿空气看作理想气体或理想混合气体,基于理想气体状态方程,焓、熵等热物性只与温度相关.Buonanno等[5]用理想气体模型计算标准大气压和-50～50℃内的饱和湿空气的热力性质参数,其计算结果误差小于0.7%.严家騄等[6]提出了比相对湿度的概念.但当超出上述范围的高温高压时,其计算结果误差明显增大.根据有限的实验数据,采用经验模型建立了量关联式,但关联式不能外推.Giacomo[7]和Davis[8]给出了湿空气密度的关联式,Garotenuto等[9]建立了增强因子和压缩因子的关联式,但建立的模型有效范围小,且热物理性质参数不够完整.半经验模型具有较充分的理论根据,且适用范围更广.Harry等[10]和Hy land等[11]选用维里方程建立了湿空气的热物性模型.上述研究者对维里系数进行计算所得到的结果相差不大,但模型的计算范围有局限性,如Harry模型不能计算0℃以下湿空气的热物理性质.

目前,对于湿空气热物理性质参数的计算离工程热物理学科领域进行科学研究及工程设计等实际需要尚有差距,主要表现在计算范围不够宽、热物理性质参数不全、计算的偏差较大或计算繁复不利于计算机程序实现以及不便于全范围分析应用等方面.因此,为适应新型热力循环科学研究及工程设计等工作的需要,进行宽温度、压力范围以及涵盖较多湿空气热物理性质参数的研究具有积极意义.

1 湿空气热力性质的计算

1.1 湿空气模型

湿空气可以看作是干空气与水蒸气混合而成的二元混合气体.干空气包含N2、O2、A r、CO2以及其他一些微量气体,因为CO2和其他微量气体的含量极其微小,笔者所采用的标准干空气不包含CO2和其他微量气体,标准干空气中N2、O2和A r的体积分数[12-14]见表1.

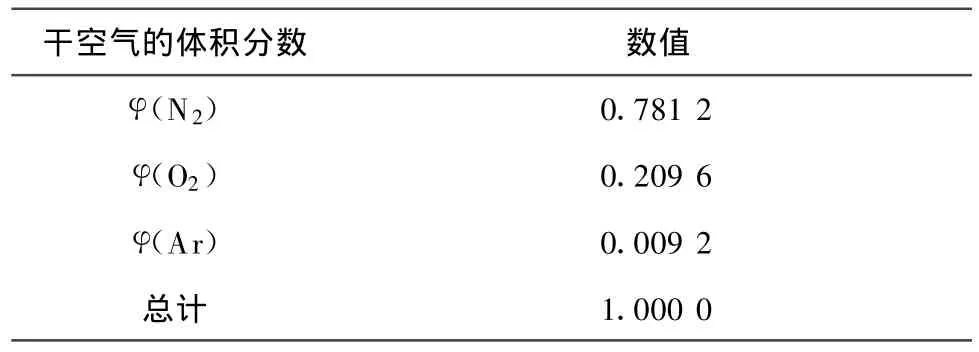
表1 标准干空气中各成分的体积分数Tab.1 Volumetric fractions of various gases in standard dry air %

N2、O2和A r均是非极性分子,水分子是具有氢键的极性分子.当压力约为单位大气压、饱和湿空气含湿量较低时,水分子氢键的缔合作用不大,此时可以将湿空气看作理想气体混合物,其组分适用理想气体状态方程,焓等热物性参数只是温度的函数.随着压力升高,水分子氢键的缔合作用逐渐加强,此时可以将干空气看作单一气体,湿空气看作水蒸气和干空气的实际二元混合气体,采用维里方程作为状态方程,建立湿空气的半经验模型.

1.2 湿空气各热力性质的计算

1.2.1 分段计算模型及其连续性

当压力为单位大气压时,实际湿空气非常接近理想气体,理想气体模型与维里模型计算得到的比焓值几乎一致.图1给出了压力为100 kPa时饱和湿空气的比焓值.

图1 压力为100 kPa时饱和湿空气的比焓值Fig.1 Specific enthalpy of saturated moist air at p MA=100 kPa

但是,维里模型采用的标准IAPWS-IF97在计算水蒸气热力性质时常会受到其计算范围的约束,只能计算0℃以上的范围;当理想气体模型在高温、高压范围内计算时,常与维里模型出现明显的偏离.为了克服这些局限,笔者采用理想气体模型和维里模型进行分段计算,结果见表2.由表2可知,两种模型在0℃处进行比焓值计算得到的结果误差很小,仅为1.4%,可以认为两种模型在此处是连续的;在压力为常压、温度为0℃时,两种模型计算的比焓值在此处的导数相差7%,因此也可以认为两种模型在此处是可微的.

表2 分界点比焓值计算的连续性Tab.2 Continuity of enthalpy calculation at demarcation point

因此,选择压力为单位大气压、温度为0℃作为分界点:当压力小于和接近单位大气压、温度低于0℃时采用理想气体模型;当压力和温度超出该范围时采用维里模型.

图2给出了压力为5 MPa时饱和湿空气的比焓值.从图2可知:在高压时,随着温度的升高,维里方程计算得到的饱和湿空气比焓值大于理想气体模型计算的饱和湿空气比焓值,并且两者的差值随着温度的升高而增大,这是因为随着温度的升高,饱和湿空气的含湿量增多,而理想气体模型仍认为含湿量只与水蒸气的分压力和饱和水蒸气压力有关,因此采用维里方程模型计算得到的含湿量大于理想气体模型计算得到的含湿量,且两者的差值随着温度的升高而增大.在高压下,随着含湿量增多,水分子间极性键的作用力更加明显,分子间距离减小,因此将水蒸气看作理想气体计算得到的饱和水蒸气分压力会偏小.

图2 压力为5 MPa时饱和湿空气的比焓值Fig.2 Specific enthalpy of saturated moist air at p MA=5 MPa

图3给出了相对湿度为50%时湿空气的比焓值.从图3可知:随着温度的升高,理想气体模型开始偏离维里模型;压力越大,理想气体模型与维里模型的偏离越明显.

图3 相对湿度为50%时饱和湿空气的比焓值Fig.3 Specific enthalpy of saturated moist air atψ=50%

图4给出了含湿量为0.002 kg/kg时的湿空气偏差焓.图5给出了压力在1 MPa时维里模型的湿空气偏差焓.分析图4和图5得到如下结论:压力越高,水分子极性键作用得到强化,分子间的距离越小,偏差焓越大;温度越高,分子动能越大,分子间距离越大,水分子极性键的作用变小,偏差焓越小.

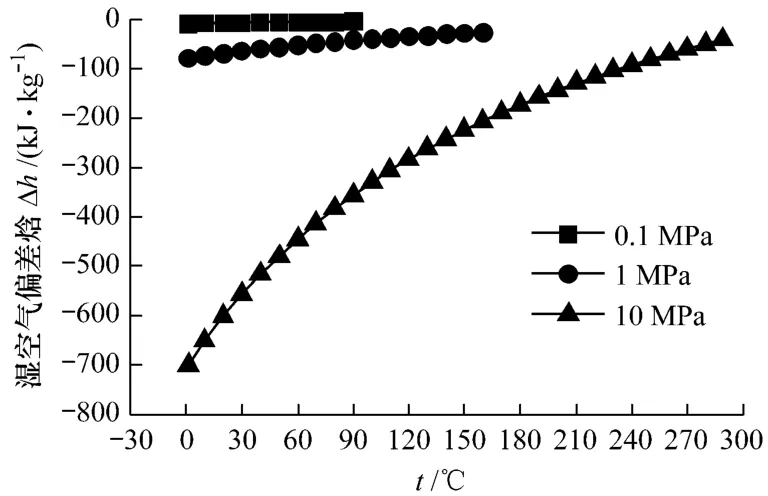
图4 含湿量为0.002 kg/kg时的湿空气偏差焓Fig.4 Enthalpy departure of moist air at d=0.002 kg/kg

图5 压力为1M Pa时维里模型的湿空气偏差焓Fig.5 Enthalpy departure of moist air at p MA=1M Pa

1.2.2 低温低压湿空气

将温度为-50～0℃、压力约为单位大气压的湿空气看作理想气体混合物,并用理想气体状态方程建立模型,比焓等热力性质只与温度有关,且计算过程简单方便.当温度低于0℃时,采用严家騄等[6]拟合的0℃以下的饱和蒸汽压力方程:

比相对湿度ψ:

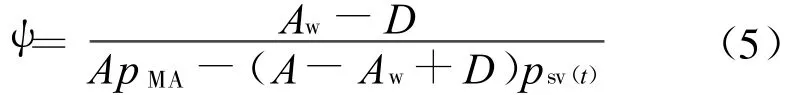
其中:参数 A、A w和D采用文献[6]的计算式进行计算.

低压湿空气露点(t d)[12]可采用式(6)迭代进行估算.

低压湿空气绝热饱和温度t w[12]可采用式(7)迭代进行估算.

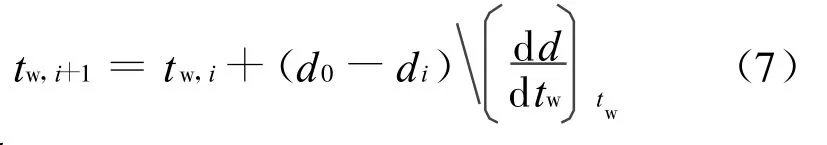
的值由式(8)近似计算.初值可取t w,1=(t+td)/2.

其中:Δt w取t w1×10-5,t w x=t w1+Δt w.

1.2.3 高温高压湿空气

对于高温高压的湿空气,强极性水分子氢键的缔合作用增大,此时压强对湿空气的焓等热力参数的影响达到不可忽视的程度,并且这种误差随着压力的增大和缔合作用的增强而加大.所以,笔者将湿空气看作干空气和水蒸气的实际二元混合气体,并采用维里方程建立湿空气的半经验模型来计算湿空气的热物理性质参数,该方法在计算湿空气比体积时具有较大的优势.

维里方程[14]

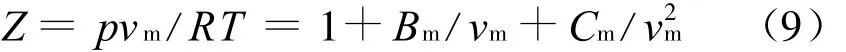
式中:Z为压缩因子;vm为湿空气比体积;Bm和Cm分别为第二、第三维里系数.

对于湿空气二元混合气体,第二和第三维里系数分别为:

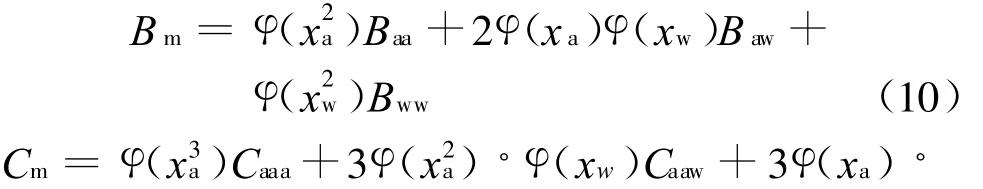
式中:φ(x a)为空气的体积分数;φ(x w)为水蒸气的体积分数.

计算第二和第三维里系数的参数采用文献[6]中的计算式.

湿空气比体积:

由维里方程推导得到比焓与比熵的计算式:

理想气体的比焓 h′a和比熵 s′a是由实际干空气的比焓和比熵[13]减去维里方程的余函数修正项得到的 ,h′w和s′w是由 IAPWS 计算得到的实际水蒸气的比焓和比熵减去维里方程的余函数修正项得到的,po是单位大气压.

高压湿空气的含湿量:

2 计算结果与分析

采用本文分段模型对压力为100 kPa饱和湿空气的热力性质参数进行计算,将水蒸气压力、含湿量和比焓值计算结果与文献[15]中数据进行了比较.

图6为压力100 kPa时饱和水蒸气的压力.由图6可知:在可比范围内(文献[15]所给出的范围),饱和蒸汽压力计算值的最大误差为4.5%,平均误差为0.3%;误差大于1%的区域仅在-20℃以下,而在这个区域内,饱和蒸汽压力低于100 Pa,其绝对误差非常小,在0～90℃区域的误差不到0.1%.

图6 压力为100 kPa时饱和水蒸气的压力Fig.6 Pressure of saturated steam at p MA=100 kPa

图7为压力在100 kPa时饱和湿空气的含湿量.从图7可知:在可比范围内(文献[15]给出的),饱和湿空气含湿量计算值的最大误差为4.5%,平均误差为0.4%,计算误差大于1%的区域集中在含湿量几乎为0 g的-20℃以下区域,大部分区域的计算误差小于0.1%.

图7 压力为100 kPa时饱和湿空气的含湿量Fig.7 Humidity ratio of saturated moist air at p MA=100 kPa

图8为压力在100 kPa时饱和湿空气的比焓值.从图8可知:在可比范围内(文献[15]所给出的范围),饱和湿空气比焓值的计算最大误差为2.1%,平均误差为0.2%,大部分区域的计算误差均小于0.1%.

图8 压力为100 kPa时饱和湿空气的比焓值Fig.8 Specific enthalpy of saturated moist air at p M A=100 kPa

利用本文介绍的湿空气热力性质计算方法可以在可比范围内计算出宽温度、压力范围的湿空气热力性质,且绘制出的焓湿图(包括温度、比焓值、水蒸气分压力、比体积、含湿量和相对湿度的等值曲线)能直观地显示出不同状态湿空气的热力性质及它们间的相互关系.图9为焓湿图.从图9可看到:当温度对应的饱和蒸汽压力高于湿空气压力时,加速上升的相对湿度曲线突然变为向右的平行直线.当湿空气温度所对应的水蒸气饱和压力高于湿空气压力时,干空气的分压力已趋于零.

图9 焓湿图Fig.9 Psychrometric chart

3 结 论

(1)根据计算范围的不同,提出湿空气热力性质分段计算方法:在低温、低压范围内采用理想气体混合物状态方程模型;在高温、高压范围内将湿空气看作干空气和水蒸气的实际二元混合气体,采用维里方程建立湿空气的半经验模型来计算湿空气的热物理性质参数.采用湿空气热力性质分段计算法一方面克服了单纯维里模型采用IAPWS-IF97计算水蒸气热力性质时,只能计算0℃以上的范围,即计算范围受到限制的问题;另一方面,在高温、高压、高湿范围,理想气体模型可以解决与维里模型出现明显偏离的局限,实现了宽温度、压力范围内的湿空气热力性质的计算(包括湿空气的相对湿度、含湿量、比体积、比热容、比焓以及比熵等).

(2)选择了分段计算方法的分界点.通过对分段计算模型计算结果的比较,表明分段计算模型在分界点处的连续性.本文的分段计算模型在低温、低压区域的计算结果具有较高的精度,能直接应用于工程计算.将高压湿空气看作实际气体,采用维里方程半经验模型进行计算可得到较好的计算结果.

(3)采用本文提出的湿空气热力性质分段计算方法能够进行全范围的理论研究、工程实际应用优化计算与设计,能够绘制出不同压力的湿空气焓湿图,且能直观地显示出不同状态湿空气的热力性质以及它们之间的相互关系,还能估算出未饱和湿空气的露点与绝热温度,且计算过程简便快捷,易于程序实现.

[1] 翁史烈,陈汉平.湿空气透平循环的基础研究[M].上海:上海交通大学出版社,2008:1-19.

[2] 肖云汉,蔡睿贤,林汝谋.HAT循环的模化与热力学评价[J].工程热物理学报,1996,17(3):255-260.XIAO Yunhan,CAI Ruixian,LIN Rumou.Globally thermodynamic model and assessment o f HAT cycle[J].Journal of Engineering Thermophysics,1996,17(3):255-260.

[3] BRIESCH M S,BANNISTER R L.A combined cycle designed to achieve greater than 60 percent efficiency[J].ASME Journal of Engineering for Gas Turbines and Power,1995,117(4):734-741.

[4] COHN A,EHRLICH S,DARGUZAS J,et al.Compressed air storage with humidication:an economic analysis[C]//ASME International Gas Turbine and Aeroengine Congress and Exhibition.Indianapolis,Indiana,USA:ASM E,1999.

[5] BUONANNO G,GAROTENUTO A A,CROV INI L,et a l.A comparison of ideal and real moist air models for calculating humidity ratio and relative humidity in the 213.15 to 473.15 K range and up a pressure of 1 M Pa[J].International Journal of thermophysics,1994,15(3):483-504.

[6] 严家騄,尚德敏.湿空气和烃燃气热力性质图表[M].北京:高等教育出版社,1989:1-20.

[7] GIACOMO P.Equation for determination of the density of moist air[J].Metrologia,1982,18:33-40.

[8] DAVISR S.Equation for determination of the density o f moist air(1981/1991)[J].Metrologia,1992,29(1):67-70.

[9] GAROTENUTO A,DELL'ISOLA M.Simplified relationships for the enhancement and compressibility factor of moist air[J].Ashrae Transactions:Research,1996,102:242-246.

[10] HARRY JS,NEISON H F,HUANG X H.High temperature properties of moist air[J].Ashrae Transactions,2001,107(2):780-791.

[11] HYLAND R W,WEXLER A.Formulations for the thermodynamic properties of dry air from 173.15 K to 473.15 K and of saturated moist air from 173.15 K to 372.15 K,at pressures to 5 MPa[J].Ashrae Transactions,1983,89(2):520-535.

[12] 刘志刚,刘咸定,赵冠春.工质热物理性质计算程序的编制及应用[M].北京:科学出版社,1992:97-109.

[13] ERICW L,RICHARD T J,STEVEN G P,et a l.Thermodynamic properties of air and mixtures of nitrogen,argon,and oxygen from 60 to 2 000 K at pressures to 2 000MPa[J].JPhys Chem Ref Data,2000,29(3):331-385.

[14] 胡英.流体的分子热力学[M].北京:高等教育出版社,1982:140-161.

[15] 沈志光.制冷工质热物理性质表和图(SI制)[M].北京:机械工业出版社,1983:86-88.