垂直轴风力机叶片翼型结冰的数值计算
李声茂, 李 岩
(东北农业大学 工程学院,哈尔滨 150030)
风力机是获取风能的关键部件,主要分为水平 轴和垂直轴两种形式.大型风力机多以水平轴螺旋桨式为主,对小型风力机而言,水平轴和垂直轴风力机都有一定的市场.近年来,垂直轴风力机,尤其是直线翼型垂直轴风力机以其结构简单、成本低廉、不需要偏航装置和便于维护等优点受到广泛关注[1-3].然而在使用中发现,当该种风力机被安装在寒冷地区时,叶片表面会出现积雪、结霜甚至结冰的现象,从而影响风力机的性能,甚至会出现事故和故障[4].笔者通过对风力机叶片野外结冰试验的观测发现,叶片表面结冰多出现在秋冬和冬春的交替季节,气温大多在-8~0°C,结冰要求空气湿度大,即空气中过冷水滴的含量很重要.试验观察发现雨夹雪的天气最容易结冰,且结冰的厚度和面积相对较大[5].目前,国内外对风力机叶片结冰问题研究较少,通常只参考一些飞机叶片结冰的计算结果,但飞机叶片与风力机的运行情况差距很大[6-8].为研究风力机叶片表面的结冰规律和影响叶片表面结冰的环境因素,笔者应用计算流体力学(CFD)方法,参照风力机叶片结冰野外观测的气候条件,主要是针对在冬季出现冻雨,即空气中水滴含量较大的情况,对直线翼垂直轴风力机叶片经常采用的NACA 0015翼型进行了翼型结冰数值模拟计算,获得了在不同风速和过冷水滴流量的条件下,8种典型攻角情况下的翼型表面结冰分布,得到翼型表面最大结冰厚度和结冰面积,并对比分析了风速、气流中的过冷水滴流量以及翼型攻角等参数对叶片表面结冰的影响.
1 计算机仿真方法
1.1 数学模型
由于小型风力机工作时的雷诺数和马赫数较小,可以将空气视作不可压缩流体.湍流模型采用k-ε双方程模型,压力-速度耦合方式采用Simp le算法.同时,在计算中添加离散相模型(DPM)来模拟空气中过冷水滴.计算基于二维不可压缩定常流体的连续性方程和动量方程,表达式如下:

式中:ρ为流体密度;xi、xj为坐标分量;ui、uj是评价相对速度的分量;p为压强;Si为生成项.
离散相模型用来计算散布在流场中的过冷水滴的运动和轨迹.在本研究的计算过程中,首先计算了空气的连续相流场,再根据流场变量来计算过冷水滴受到的作用力,并确定其运动轨迹.
在计算翼型结冰过程中,对过冷水滴进行如下假设:①水滴均匀分布,以球形存在,运动过程中水滴尺寸保持不变;②温度、黏性和密度等介质参数在水滴运动过程中保持不变;③水滴的初始速度与自由流的速度相等,水滴体积很小以至于它们的绕流不会影响流场的性质;④悬浮在运动空气中水滴的附加质量力、压差力、Saffman升力等与气体阻力和重力相比可以忽略.
根据牛顿第二定律,水滴运动方程为:

式中:md为水滴质量;ρa为空气密度;Cd为阻力系数;u为当地气流速度;u d为水滴速度;A d为水滴的迎风面积.
式(3)经整理后可简化为:
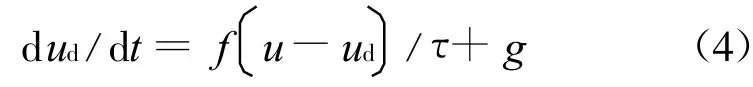
获得水滴运动速度后,对其积分即可获得水滴运动轨迹.
1.2 计算方法
叶片翼型选择直线翼垂直轴风力机通常采用的NACA 0015对称翼型,叶片翼型周围网格采用三角形网格,如图1所示.叶片翼型弦长c为30 mm.流场计算范围如图2所示.

图1 叶片翼型周围网格Fig.1 G rid division around the blade aerofoil

图2 计算范围Fig.2 Flow field area for com putation
1.3 计算条件
计算条件如表1所示.水滴流量是指在气流中加入的过冷水滴的流量,该参数代表液滴含量(liquid water content,LWC).LWC是 ISO12494—2001中规定的大气中物体结冰时的水滴含量参数.本文选取的水滴流量值相当于冬季有小冻雨时的情况,湿度在90%以上,依据是风力机野外结冰试验的报告[5].通常,有关结冰的风洞试验多是采用控制水滴流量的方法,所以本文亦采用水滴流量作为参数.设定风速有3种,为风力机通常的工作风速.选用3种风速是为了比较雷诺数的影响.翼型攻角α的定义见图3.直线翼垂直轴风力机与水平轴风力机不同,其叶片攻角在0°~180°.所以本研究选取了8种典型的攻角,包括翼型前缘迎风和尾缘迎风的各4种角度.

表1 计算条件Tab.1 Computational conditions
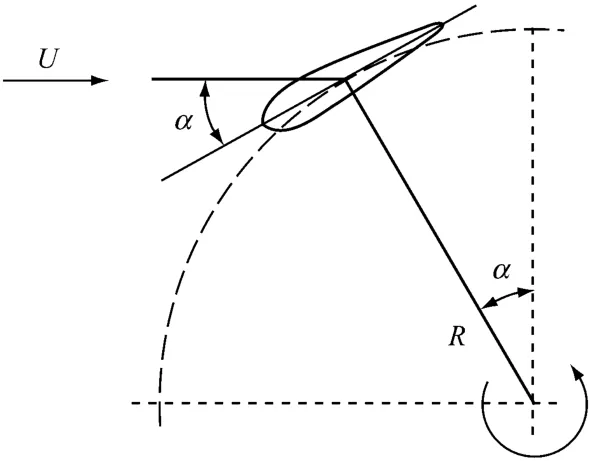
图3 叶片攻角的定义Fig.3 Definition of blade attack angle
2 计算结果与分析
2.1 攻角的影响
图4给出了风速U=4m/s、水滴流量Q=1 L/min时在各攻角下的翼型表面结冰分布情况.从图4中可以看出,在其他条件相同的情况下,攻角不同时,翼型表面的结冰情况也不同.当攻角为0°时,翼型上下表面结冰分布基本一致,冰面生长得比较均匀,一直从前缘至尾缘,冰层厚度也较一致.当攻角为10°时,上下表面的冰层发生了很大变化.前缘结冰明显增多,冰层累积得很厚,且冰层在上表面的分布明显多于下表面,但上表面的冰层没有生长到尾缘,只是到翼型中部位置为止.当攻角为30°时,翼型前缘的结冰厚度小于攻角为10°时的情况,但上表面的结冰一直生长到尾缘附近,且在下表面的尾缘附近也有一定的结冰.
当翼型尾缘迎风时,翼型表面的结冰情况与前缘迎风时有很大不同.当攻角为180°时,翼型表面的结冰只集中在尾缘附近很小的范围内,冰层比较厚,且有迎风生长的趋势.攻角为170°时与攻角为180°时的情况类似,结冰的情况没有因为攻角变化而发生很大变化,结冰还是主要集中在尾缘附近很小的范围,这与前缘迎风时的情况有很大差别.当攻角为150°时,翼型下表面完全结冰,并一直延伸至前缘附近,而且冰层较厚,但上表面的结冰很少,只在前缘附近有少量的结冰.

图4 各攻角下叶片翼型表面结冰分布情况Fig.4 Icing on blade surface at various attack angles
2.2 水滴流量和风速的影响
以翼型前缘迎风、攻角45°(图5)和尾缘迎风、攻角135°(图6)情况为例,分析水滴流量和风速对翼型表面结冰的影响.
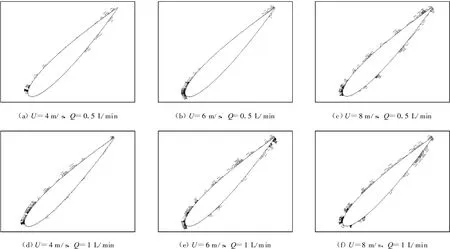
图5 不同风速和水滴流量时叶片翼型表面结冰分布情况(α=45°)Fig.5 Icing on b lade surface at various wind speeds and liquid water contents(α=45°)
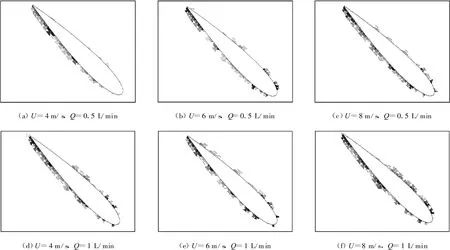
图6 不同风速和水滴流量时叶片翼型表面结冰分布情况(α=135°)Fig.6 Icing on b lade surface at various wind speeds and liquid water contents(α=135°)
由图5可知,翼型前缘迎风时,在同一风速下,空气中水滴流量对翼型表面结冰的影响很大.图5(d)大水滴流量情况下翼型前缘部分和上表面的结冰明显比图5(a)小水滴流量情况时的结冰面积大,甚至比图5(b)小水滴流量、风速6 m/s时结冰还要多.该趋势也可从图5(e)、图5(b)和图5(c)的比较中发现.但当风速从4m/s增加至8 m/s时,图5(c)所示的翼型表面结冰面积明显比图5(d)所示的结冰面积大.由此可以推论出,对于翼型前缘迎风的情况,空气中的水滴流量和风速都是影响翼型表面结冰的关键因素.在低风速时,流量的影响起主导作用,而当风速较高时,风速对结冰的影响也起到关键作用.
尾缘迎风时的情况与前缘迎风时有一定的差别(图6).不同风速和水滴流量对翼型表面结冰的影响主要体现在翼型背风面的结冰面积上.增大水滴流量和风速都可以使翼型背风面结冰增多,而迎风面的结冰情况变化不大.
2.3 前缘与尾缘处最大结冰厚度
为了定量分析各因素对叶片表面结冰的影响,定义无量纲系数:冰厚比β,即翼型前(尾)缘最大结冰厚度与叶片弦长之比,如式(5):
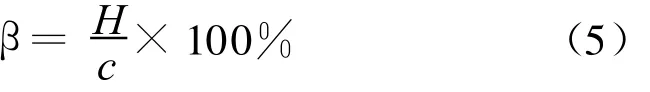
式中:H为前(尾)缘处的最大结冰厚度;c为叶片弦长.
图7和图8给出了各计算条件下的冰厚比.总体来看,无论是翼型前缘还是尾缘处的最大结冰厚度均占翼型弦长的4%以内,但前缘迎风和尾缘迎风时的冰厚比变化规律存在很大差别.当叶片前缘迎风时(图7),无论水滴流量的大小,攻角0°时的冰厚比最小,只有1%,10°时最大,可达 4%,而攻角为30°和45°时,冰厚比维持在2%~ 3%.可见,当前缘迎风时,前缘的最大结冰厚度不随着攻角的增大而增大.另外,由图7(a)可知,当水滴流量较小时,风速的增加有时并不会使翼型前缘结冰厚度增加,如攻角为 10°和30°的情况.由此可知,水滴流量对结冰厚度起关键作用.对于尾缘迎风的情况(图8),各攻角的情况比较类似,冰厚比均在3%~4%.可见与前缘迎风不同,尾缘迎风时,水滴流量和风速对翼型尾缘部分的结冰影响不大.

图7 前缘迎风时叶片翼型冰厚比Fig.7 Icing thickness ratio at leading edge of aerofoil
2.4 翼型表面结冰面积
为了分析在不同条件下翼型表面的结冰面积,定义另一个无量纲系数:结冰面积比γ,即翼型表面结冰的面积与翼型面积之比,如式(6)所示:

图8 尾缘迎风时叶片翼型冰厚比Fig.8 Icing thickness ratio at trailing edge of aerofoil

式中:A1为结冰面积;A为翼型面积.
图9和图10给出了各计算条件下的翼型结冰面积比.当前缘迎风时,在4 m/s较小风速情况下,不论水滴流量的大小,攻角0°时的结冰面积最小,30°时最大.增大风速对攻角 0°和10°时的结冰影响较小,但对大攻角(30°和45°)时的影响很大.尤其是风速为8m/s时,其结冰面积的变化趋势发生了变化.这说明在大攻角和雷诺数较大时,翼型表面的结冰情况变得很复杂.另外,从数值计算的方法来考虑,由于大攻角时翼型背面的流场变得复杂,其计算误差也逐渐增大,再加之有结冰的计算,因此,大攻角时的计算结果可能存在一定程度的误差,这需要在后续的研究中加以解决.但目前本研究的主要目的在于对比分析,因此该计算结果仍具有一定的参考价值.

图9 前缘迎风时叶片翼型结冰面积比Fig.9 Icing area ratio at leading edge of aerofoil
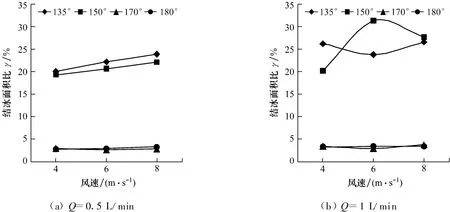
图10 尾缘迎风时叶片翼型结冰面积比Fig.10 Icing area ratio at trailing edge of aerofoil
当尾缘迎风时,攻角170°和180°时的结冰面积情况非常相似,而攻角 135°和 150°时的结冰面积变化要大很多.而且当水滴流量不同时,结冰面积也有很大不同.当水滴流量较小时,结冰面积呈现出一定的线性关系;当水滴流量增大时,变化规律变得很复杂.
当攻角很大时,翼型表面结冰面积变化规律变得复杂,但从总体来看,在一定攻角范围内,翼型表面的结冰面积随翼型迎风面积、风速和空气中水滴流量的增加而增大.在本研究的计算条件下,翼型表面的结冰面积最大可达到翼型面积的32%,而最小也超过3%.因此,翼型结冰后必将对翼型的载荷分布产生影响,使得叶片受力和气动特性发生变化.
3 结 论
(1)气流中所含的过冷水滴量和风速是影响风力机翼型表面结冰及其在叶片表面生长的关键因素.在低风速时,水滴流量的影响占主导作用.
(2)翼型攻角不同,其表面结冰的厚度、面积和其生长趋势也不同.尤其是在前缘和尾缘处的结冰规律有很大不同.
(3)从总体来看,在一定攻角范围内,翼型表面的结冰面积随翼型迎风面积、风速和空气中水滴流量的增加而增大.在一定条件下,结冰面积可达到翼型面积的30%以上.
[1] ISLAM M,TING D S K,FARTAJ A.Aerodynamic models for Darrieus-type straight-bladed vertical axis wind turbines[J].Renewable and Sustainable Energy Reviews,2008,12(4):1087-1109.
[2] PARASCHIVOIU I.Wind turbine design with emphasis on Darrieus concept[M].Montreal,Canada:Polytechnic International Press,2002.
[3] 李岩.垂直轴风力机技术讲座(一):垂直轴风力机及其发展概况[J].可再生能源,2009,27(1):121-123.LI Yan.vertical axis wind turbine technical lecture(1):Vertical axis wind turbine and its development[J].Renewable Energy Resources,2009,27(1):121-123.
[4] 李岩,田川公太郎.叶片附着物对直线翼垂直轴风力机性能影响的实验研究[J].动力工程,2009,26(3):31-33.LI Yan,KOTARO Tagawa.wind tunnel test on the effects of attachment on blade surface of a SB-VAW T[J].Journal of Power Engineering,2009,26(3):31-33.
[5] 杨柏松,李岩,冯放,等.直线翼垂直轴风力机静态叶片结冰的观测与分析[J].可再生能源,2009,27(6):20-23.YANG Baisong,LI Yan,FENG Fang,et a l.Observation and analysis of icing on static blade of straightbladed vertical axis wind turbine[J].Renewable Energy Resources,2009,27(6):20-23.
[6] 张大林,陈维建.飞机机翼表面霜状冰结冰过程的数值模拟[J].航空动力学报,2004,19(1):137-141.ZHANG Dalin,CHEN Weijian.Numerical simulation of rime ice accretion process on airfoil[J].Journal of Aerospace Power,2004,19(1):137-141.
[7] 陈维建,张大林.瘤状结冰过程的数值模拟[J].航空动力学报,2005,20(3):472-476.CHEN Weijian,ZHANG Dalin.Numerical simulation of glaze ice accretion process[J].Journal of Aerospace Power,2005,20(3):472-476.
[8] BRAGG M B,BROEREN A P,BLUMENTHAL L A.Iced-airfoil aerodynam ics[J].Progress in Aerospace Sciences,2005,41(5):323-362.

