下承式钢箱系杆拱桥局部结构有限元分析

吕成林，曾 嵩，向明航，陈 璨

(重庆交通大学土木建筑学院，重庆400074)

近年来，下承式钢箱系杆拱桥在我国发展得很快，其具有良好的受力性能，造型优美，并具有钢结构自重轻、建筑高度小、跨越能力大、施工周期短等特点，因而此种桥梁在跨越高等级公路及河流的桥梁中具有较好的优越性，尤其是应用在跨度为100～150m范围内的城市主干道、高速公路和铁路中。钢箱系杆拱桥是一个受力十分明确的结构，其各部分构造要求传力明确且有足够的强度和刚度，各部分构造既重要又复杂，因此在进行此类桥梁设计时，有必要对各局部结构的受力情况进行分析。本文结合江津滨江新城滨州路一号桥，对其吊杆锚固结构进行有限元分析。

1 工程概况

江津滨江新城滨州路一号桥是滨洲路上的一座重要的城市桥梁。其桥型为主跨120m的下承式钢箱系杆拱桥。桥横向全宽35m，纵坡为2.549%。拱肋为钢箱结构，跨径120m，计算矢高37.2m，矢跨比1/3.2。拱肋截面为等截面箱型截面，顶、底板厚度为32mm，腹板厚度为24mm。其中拱肋高2.8m，宽1.8m。拱轴线根据吊杆的索力和高低拱脚情况，按实际压力线确定拱轴线。拱轴线由多段直线形成，直线与直线之间用圆曲线过渡。吊杆与拱肋锚固连接处局部结构如图1所示。

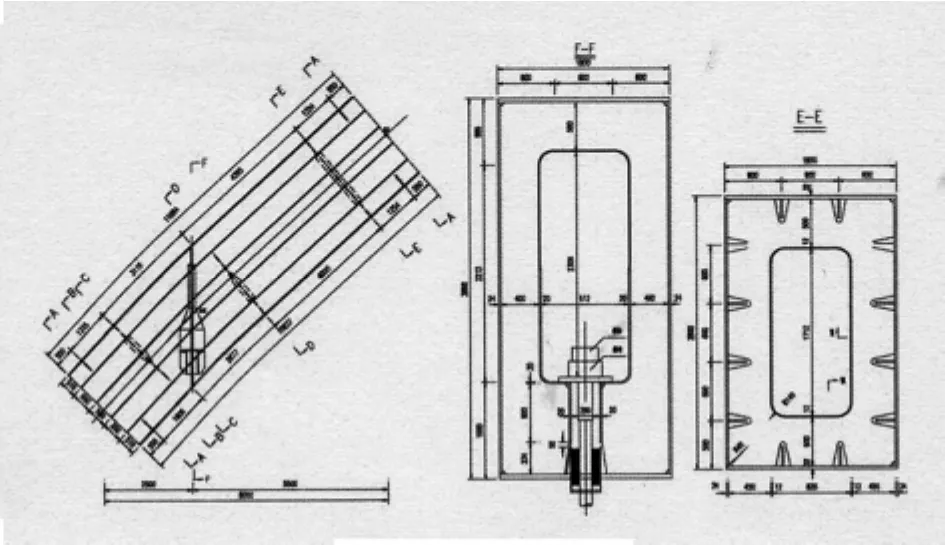
图1 局部结构图

2 局部模型的建立与计算方法

2.1 计算方法

局部模型受力以及约束状态都受到全桥模型结果的影响，因此在进行局部分析时，必须先计算出全桥整体分析所得的吊杆内力，再根据圣维南原理将各杆件内力静力等效地加在局部模型上，在局部模型上再加上相应的位移约束条件，计算可反映局部受力的应力分布情况。本模型采用ANSYS软件建立模型并划分网格产生局部有限元模型，根据全桥有限元分析结果确定局部分析的荷载及边界条件，然后把整体分析计算所得的相关吊杆内力，作为外力加在节点局部模型上进行计算，分析节点应力水平和分布情况。计算理论采用弹塑性非线性理论，应用弧长法进行迭代计算。

2.2 建立局部模型

根据全桥的计算结果选取具有代表性的节段，本模型选取拱脚处第一个吊杆与钢箱拱肋锚固连接处作为计算模型。连接处各个板件包括:拱肋顶板、底板和腹板，横隔板和加劲肋，圆管、锚杯等。其中拱肋高2.8m，宽1.8m。为了提高计算效率对结构进行适当简化，钢箱拱部分计算长度取标准长度8m。钢箱拱、横隔板以及加劲肋采用SHELL181板壳单元。材料采用Q345D钢材，其弹性模量取2.1×105MPa，泊松比取 0.3，屈服强度345 MPa。模型一:圆管与拱肋底板不连接。模型二:圆管与拱肋底板连接成整体。其局部模型如图2所示。

2.3 边界条件以及加载方法

计算模型以拱肋轴向为X轴，横桥向为Y轴，竖向为Z轴。其模型边界条件为，约束拱肋前端部截面的X轴、Y轴、Z轴方向位移及绕X轴转角，约束拱肋后端部截面的Y轴方向位移，Z轴方向位移。

根据有限元软件Midas/Civil对全桥在一期恒载+二期恒载+全桥双线满布荷载作用下计算出吊杆的最大索力作为外荷载进行局部分析。

加载方法为锚垫板与螺母重叠处节点与截面中心节点刚性连接，并在中心节点施加吊杆方向的荷载。

3 计算结果分析

3.1 计算结果

吊杆锚固结构局部模型极限承载力计算结果显示，模型一:锚固位置圆管周边横隔板部分截面开始屈服时强度为5368kN，全截面屈服强度为9282kN。模型二:锚固位置圆管周边横隔板部分截面开始屈服时强度为5371kN，全截面屈服强度为12170kN。

图2 局部模型图

吊杆锚固结构加载点的荷载/索力－位移曲线如图3所示。图中竖坐标表示加载节点的荷载与最大索力的比值，横坐标表示加载节点的加载方向位移(mm)。

图3 加载点的荷载/索力－位移图

两种模型局部结构的von Mises应力分布分别如图4、图5所示step1(荷载大小为最大索力)即荷载达到4300kN时锚固位置圆管周边横隔板部分截面及底板的应力分布情况;step2即加载结束时锚固位置圆管周边横隔板截面及底板的应力分布情况。

图4 模型一局部结构Von Mises应力分布图(×10－3MPa)

3.2 结果分析

根据上面两种模型的计算结果，对其局部结构的受力进行比较分析。

由图3可知，两种模型的荷载/索力－位移曲线都是由直线段和曲线段构成，即结构受力先进入弹性阶段，然后进入塑性阶段，满足弹塑性非线性理论。

当结构加载时，加载点开始发生位移，结构开始发生微小变形。随着荷载的不断加大，加载点位移逐渐变大，当荷载达到最大索力4300kN时，模型一加载点的位移为2.00mm，模型二的位移为1.96mm，两者相差0.04mm。当荷载继续加大直到极限承载力时，材料进入塑性阶段，结构发生破坏，此时模型一加载点的位移为5.78mm，模型二的位移为12.10mm，比前者位移大6.32mm。

由图4可知，荷载为step1时，模型一吊杆锚固结构的应力分布较均匀，锚固处结构的最大等效应力达到345Mpa，出现在锚固位置横隔板小部分截面上;其它大部分区域的等效应力在115MPa以下;锚固位置下方及圆管周边的横隔板应力水平稍高些，应力值主要在115～191Mpa之间;横隔板与圆管下端连接区域应力值较大，达230Mpa;拱肋底板与横隔板连接区域等效应力值都在76 Mpa以下。荷载为step2时，结构进入破坏状态，锚固位置圆管部分截面以及周边横隔板部分截面已屈服，其它大部分区域的等效应力在76～268Mpa之间;横隔板与圆管下端连接区域已经屈服;拱肋底板与横隔板连接区域等效应力值不大，在38～153Mpa之间。

图5 模型二局部结构Von Mises应力分布图(×10－3MPa)

由图5可知，荷载为step1时，模型二吊杆锚固结构的最大等效应力为337Mpa，出现在锚固位置横隔板小部分截面上;其它大部分区域的等效应力在112MPa以下;锚固位置下方及圆管周边的横隔板应力值主要在112～187Mpa之间。拱肋底板与横隔板连接区域等效应力值不大在75 Mpa以下，而与圆管连接区域应力值较大，最大达到112Mpa。荷载为step2时，结构进入破坏状态，锚固位置圆管大部分截面以及周边横隔板大部分截面已全截面屈服，其它大部分区域的等效应力在77～269Mpa之间，且圆管受压变形严重;拱肋底板与横隔板连接区域等效应力值在39～230Mpa之间，而与圆管连接区域已经屈服。

4 结论

通过以上计算结果分析表明:

⑴当荷载达到最大索力时，模型一最大等效应力达到屈服应力345Mpa，比模型二大。出现的位置基本相同，且整体应力水平相当，局部变形很小。

⑵当荷载达到极限承载力时，模型二结构屈服区域比模型一大，且局部变形也比较大，尤其是圆管受压变形。

⑶模型一中拱肋底板的应力水平较低，横隔板的应力分布较均匀，横隔板与圆管下端连接处有应力集中现象。

⑷模型二中圆管对拱肋底板的影响比较大，底板的应力水平较高，变形大，圆管与底板连接处容易出现应力集中。

⑸模型一的极限承载力虽比模型二小，但满足设计要求;其吊杆锚固结构受力合理，传力顺畅，且进入破坏模态时，局部变形较小，稳定性好。

［1］顾安邦.桥梁工程［M］.北京:人民交通出版社，1999.

［2］陈建荣，张捷，王吉英，等.钢箱拱肋系杆拱桥的稳定分析［J］.铁道建筑，2007(4):4－5.

［3］王月.140m下承式钢箱系杆拱桥关键部位局部受力分析［D］.长沙:中南大学，2009.

［4］叶梅新，李一可.下承式钢箱系杆拱桥拱脚局部受力分析［J］.西部探矿工程，2007(7):65－67.

［5］郭建勋，袁明，陈列，等.福厦铁路钢箱系杆拱桥设计构思与研究［J］.桥梁建设，2006(S2):97－04.

［6］郭建勋，袁明，陈列，等.福厦铁路钢箱系杆拱桥设计构思与研究［J］.桥梁建设，2006(S2):97－04.

［7］黄帅.下承式钢箱拱肋系杆拱桥受力性能研究［D］.西安:长安大学，2010.

［8］金福海，文功启，徐勇.武广铁路客运专线140m钢箱系杆拱桥设计及其在高速铁路中的应用［J］.桥梁，2010(1):107－110.