通勤班车出行线路优化研究＊

韩 艳 关宏志 赵红征

（北京工业大学交通工程北京市重点实验室 北京 100124）

单位通勤班车（以下简称班车）作为城市公共交通方式之一，属于辅助公共交通系统［1］.近年来国内外学者们从多角度对班车线路进行研究.Jerby Shai［2］等对中央火车站循环线路设置进行优化设计研究.郭强［3］等人以社区儿童接送服务车辆的路线优化问题为研究对象，建立了多目标非线性整数规划模型，通过启发式最优算法找出最优路径.王细元［4］等人对GIS技术应用于超市班车线路优化进行研究.宇仁德［5］基于企业运营的总消耗费用最小的优化原则对最佳通勤车车辆数的确定进行了研究.本文对通勤班车出行者出行特性进行调查，建立了基于多项Logit模型的通勤班车前端衔接方式模型，确定班车出行者班车前端出行方式和衔接时间，并以满足最大出行需求、班车出行者总体通行时间最小为路径寻优的双重目标，建立了通勤班车线路优化模型.

1 班车运营特点及线路设置要求

班车主要是单位通过购置或租赁社会车辆用于接送本单位职工上下班、团体公务活动的9座（含）以上客车.利用班车出行总时间可分为两部分：出发点至班车站点时间t1和各站点至单位运行时间t2.因此，对于每一位通勤出行者而言，需要考虑采取何种交通方式到达某条班车线路的某站点和出发时间，同时考虑该出发时间是否早于自己的意愿最早出发时间，与其他出行方式相比，班车效用是否具备优越性.而上述问题属于通勤出行者出行方式及班车出行前端衔接方式选择问题.基于班车运营特性及班车出行者特性做如下假设.

假设1.班车使用者希望尽可能迅速地从家到达班车站点.

假设2.班车使用者通常就近选择班车站点换乘班车，确保班车发车时间之前达到班车站点，并希望出发时间不早于意愿最早出发时间，对从其他交通方式转向班车的出行者而言尤其如此.

假设3.为了保证足够的服务水平，线路设计应确保运行时间符合预先确定的时间限制.因此，班车线路运营沿途实现大站停靠，路线不能重复，且为往返线路.

2 班车前端衔接方式选择模型

2.1 班车出行行为调查及分析

基于上述分析，为研究班车线路优化问题，需先对班车出行者的出行行为（revealed preference，RP调查）进行调查［6］.调查问卷主要包括如下：（1）乘客基本信息（性别、年龄、收入、小汽车拥有情况等）；（2）利用班车出行信息.乘车频率（次／周）、出发时间、家至班车点的出行时间出发地地铁线路可利用情况、行程时间、出行方式（步行、公交、地铁）、交通费用等；（3）意向调查.可以接受的最早出发时间、对原班车线路站点调整，乘客选择意向线路及站点.

调查于2009年4月工作日开展，采取面对面调查方式.调查结果表明，约93%的班车通勤者乘坐频率在每周3次以上；班车出行者家至单位的距离30km以内约占70%；从图1可看出步行在衔接方式中占59.22%，地铁约7%；67%的人可以在20min之内达到班车站点，8%的乘客需50min以上的时间.约占78.1%的班车出行者前端衔接时间占总出行时间的比例主要集中在0.2～0.5之间；从图2可看出85%以上的班车出行者希望（容忍）最早出发时间不早于实际出发时间，通过线路优化站点合理设置来减少出行时间.

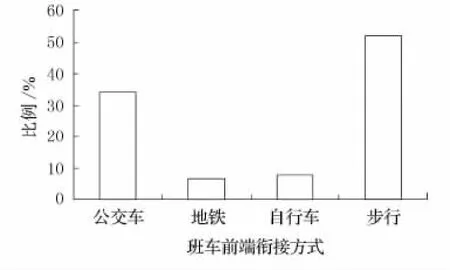
图1 衔接方式分布图

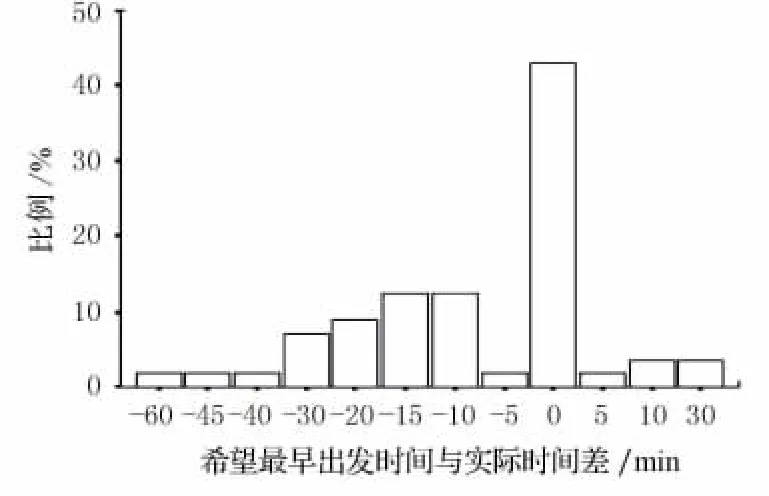
图2 希望最早出发时间与实际出发时间差

2.2 出行前端方式选择模型

通勤者到达班车站点，属于前端衔接，因后端交通方式单一，因此选用ML（multinomial logit）模型来预测前端衔接方式，以确定前端衔接时间，为班车线路优化设计提供准确的数据［7］.通过调查分析，本文选择步行、公交车、地铁3种交通方式作为ML模型的选择肢.对代入模型中的自变量进行筛选，经过模型检验，最终标定结果如表1所列.从模型的标定的结果可以看出，均达到0.40以上，表明模型精度较高.

表1 ML模型标定结果表

3 班车线路优化模型

3.1 优化目标

在班车用户需求调查的基础上，对班车线路进行设置或对已有线路进行优化调整.班车线路优化目标包含了运输管理机构、乘客、班车设置单位三者的目标.

1）运输管理机构 通常是满足最大需求反应，希望通过班车站点及线路的优化设计，吸引更多的通勤出行者由其他交通方式转向班车出行，尤其是小汽车使用者.

2）乘客 出发时间不早于自己的意愿最早出发时间.

3）班车设置单位 出于经济效益考虑，提高班车运营效率和利用率，满足职工通勤出行需求，并能够降低通勤费用.

上述目标整合为：对于城市路网，班车线路应设计用来最大程度地覆盖乘客从各个路网需求中心至交通中心的潜在需求，并确保整条线路运行的时间不要超过某阈值.

3.2 班车线路优化流程

基于上述原则，班车线路设计分为如下6步：（1）城市路网特性分布，获取班车路线设计的基本路网；（2）获取路网各节点间的平均运行速度；（3）确定班车线路服务范围；（4）确定班车线路上潜在的出行需求；（5）班车线路设置及调整方案；（6）线路目标优化及其求解.优化流程如图3所示.

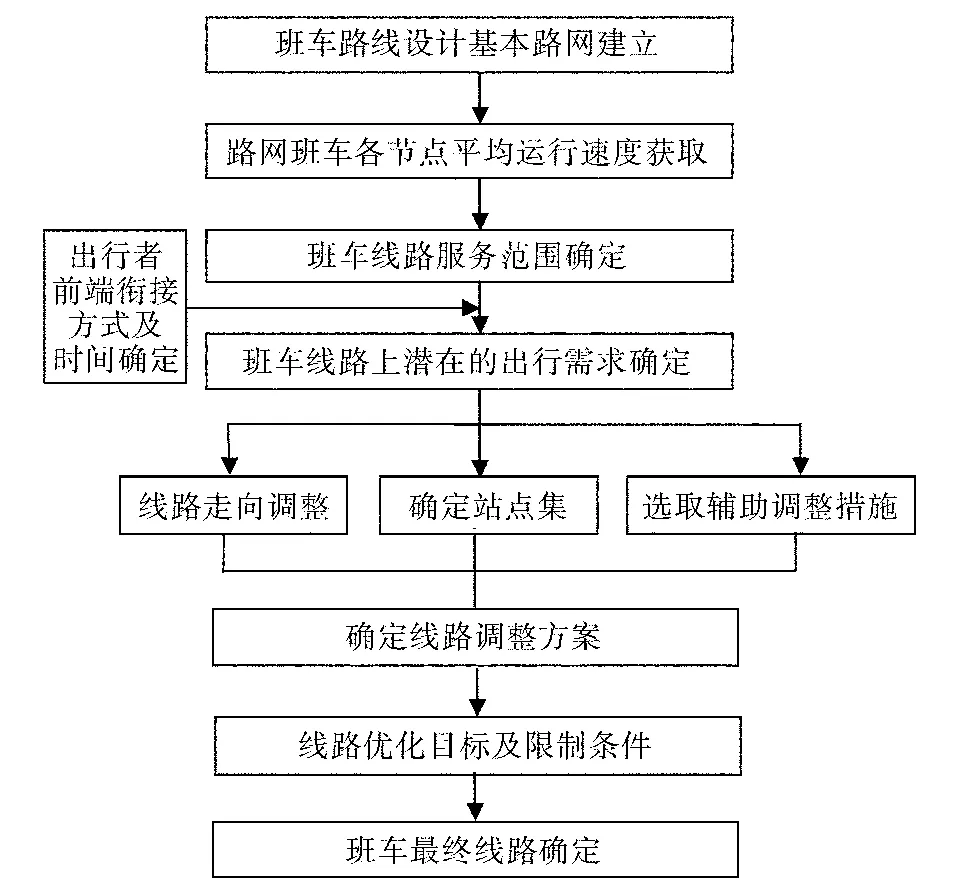
图3 优化调整流程图

3.3 优化模型

设G（N，A）为城市路网，节点N＝｛1，2，…，n｝，路段A＝｛（i，j）：i，j∈N；i≠j｝，对于每一路段（i，j）∈A，车辆运行时间tij根据路网历史交通资料获知.

以满足最大出行需求，乘客总体时间最小为目标函数来达到线路优化.其目标函数为

式中：tij为从站点i到站点j的时间，i，j∈｛站点集｝；tmoi为第m 个乘客从出发端到达班车站点i的时间；dmi为第m个人到达i点的距离；Rm为班车到达终点的最晚时刻；Tm为乘客现状出发时刻为乘客可接受最早出发时刻；Mmax为班车的容量.

模型中定义式（1）决策变量yij以表征通勤班车线路是否经过路段（i，j），Ymi表征乘客m 是否选择在站点i乘车的决策变量.式（2）为线路的最长运行时间限制；式（3）为站点有乘客上车的约束；式（4）为乘客只能选择一个站点乘车的约束；式（5）为车辆容量约束；式（6）定义S为路网节点组合，每个节点组合中至少包含两个节点，并且不包括终点n1.式（7）确保线路中路段数量少于节点数量，避免部分线路重复；式（8）乘客出发时刻的约束以及式（9）、（10）相关变量的0－1约束和非负整数约束.通过启发式算法［9］，可对班车线路优化模型进行求解.

4 案 例

本文的班车线路网络在无事故或异常天气的正常条件下，基础路网如图4所示，各边的时间参数和节点的上车人数参数作为边单元属性文件进行设定.其中1为终点，各站点间间距为dij，根据历史交通量数据，各站点间运行时间为tij，对于每一位通勤出勤者m，其可选的交通方式有常规公交、地铁和步行，其相应的时间和费用分别为｛trail，Crail｝、｛tbus，Cbus｝和｛twaik，Cwaik｝，每个人最早的意愿出发时间为T′m，班车到达终点的最晚时刻Rm为07：50，班车容量限制为45人，班车运营时长限制为50min.

根据乘客的基本资料数据，利用ML模型，可计算出每位乘客自出发点至意愿班车站点i的采取的交通方式，相应的时间tmoi和费用及其出发时刻，并可初步统计出各站点的意愿乘客数

将以上数据代入目标函数中，得出相应线路的总体运行时间及乘客数，其中满足约束条件的为：4－5－6－3－2－1，4－3－2－7－1，6－7－2－1.根据满足最大需求，总体时间最少的目标函数可知，4－5－6－3－2－1为最优线路（见图5）.

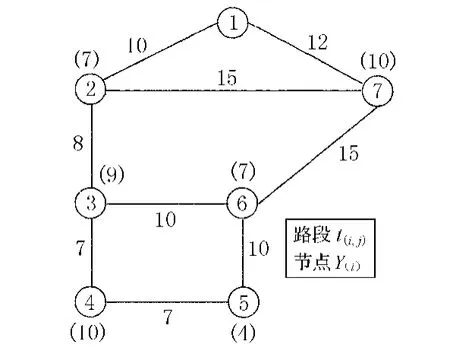
图4 基本路网图

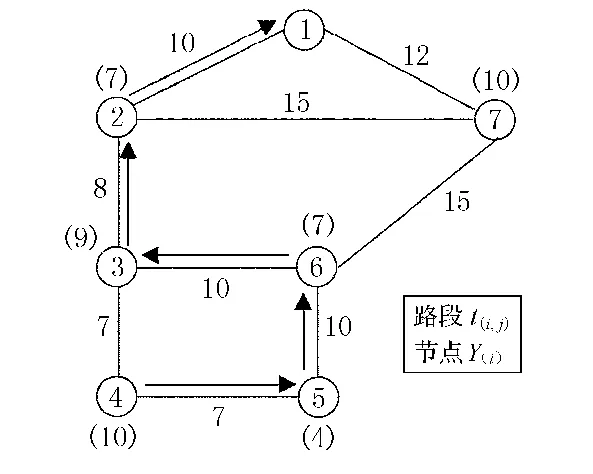
图5 优化路线图

5 结束语

论文对通勤班车出行者出行特性进行了调查，约占78.1%的班车出行者前端衔接时间占总出行时间的比例主要集中在0.2～0.5之间；85%以上的班车出行者希望（容忍）最早出发时间不早于实际出发时间，希望通过线路优化站点合理设置来减少出行时间，建立了基于ML模型的通勤班车前端衔接方式模型，计算每位班车出行者班车前端衔接时间，并建立了以满足最大需求、班车出行者总体通行时间最小为路径寻优的双重目标的班车线路优化模型，路径寻优过程中考虑出勤者出发时间不早于意愿最早出发时间.通过启发式算法对班车线路优化模型进行求解，通过实例表明启发式算法的合理性及有效性，可通过通勤班车线路的优化设置来提高公共交通出行.

［1］Yan H，Hongzhi G.Study on models of commuter mode choice beyond fuel prices based on ordered logit models［J］.Journal of American Science，2010，6（8）：230－235.

［2］Shai J，Ceder A.Optimal routing design for shuttle bus service［J］.Transportation Research Record，2006，1971：14－22.

［3］郭 强，李育安，郭耀煌.社区儿童接送服务车辆的线路优化［J］.西南交通大学学报，2006.41（4）：486－490.

［4］王细元.超市免费班车最优路线的选择［J］.技术与市场，2007（6）：86－87.

［5］宇仁德，刘 晃.最佳通勤车车辆数的确定［J］.山东工程学院学报，2000，6（2）：66－68.

［6］关宏志.非集计模型－交通行为分析的工具［M］.北京：人民交通出版社，2004.

［7］殷焕焕，关宏志，秦焕美.基于非集计模型的居民出行方式选择行为研究［J］.武汉理工大学学报：交通科学与工程版，2010，34（5）：1 000－1 003.