内燃机连杆机构的建模与运动仿真

万苏文，陶 莉，刘永利

WAN Su-wen1,TAO Li2,LIU Yong-li1

（1. 淮安信息职业技术学院，淮安 223001；2. 淮阴工学院，淮安 223001）

0 引言

曲柄连杆机构是内燃机实现工作循环、完成能量转换的传动机构，既是用来传递力和改变运动方式的最关键组成部分之一，也是构成往复运动活塞式内燃机的基础机构组成。柴油机曲柄连杆机构由活塞组、连杆组和曲轴飞轮组等三大部件组成。其中活塞组包括活塞、气环、油环、活塞销、销挡圈等零件，沿气缸做往复直线运动；连杆组由连杆及附件组成，做平面运动；曲轴飞轮组包括曲轴、飞轮等，绕曲轴轴线做旋转运动，具体组成如图1所示。由于该机构是在高温高压下作变速运动，其工作过程中的受力情况非常复杂，其中有作用在活塞顶部的气体作用力、运动零件的质量惯性力与离心力、各摩擦表面的摩擦力以及外界阻力等，因此在分析和设计内燃机连杆机构的结构强度、刚度等方面带来了巨大挑战，传统的分析方法是采用解析法或图解法，人工计算量大、耗时、易出错和不直观，随着Pro/E和MATLAB等软件的发展，现在可以利用软件工具进行机构建模与分析，从而能够快速、精确、直观地反映机构的运动和受力情况。本文以MATLAB为研究工具，用闭环矢量二介导数法建立曲柄滑块机构的数学模型，应用Simulink模块建立仿真模型；同时以Pro/ENGINEER为研究工具，创建实体零件及其装配模型，如图2所示为单缸内燃机的Pro/E结构图。同时推导出活塞对气缸的侧向力、活塞的惯性力、连杆对活塞的作用力以及内燃机的转矩等方程式。这样的研究方法可以应用于各种机构的运动分析，对内燃机活塞环和气缸套摩擦力大、使用寿命低、发动机噪音大、燃油热效率不高等问题也具有广泛的意义。

图1 柴油机曲柄连杆机构组成

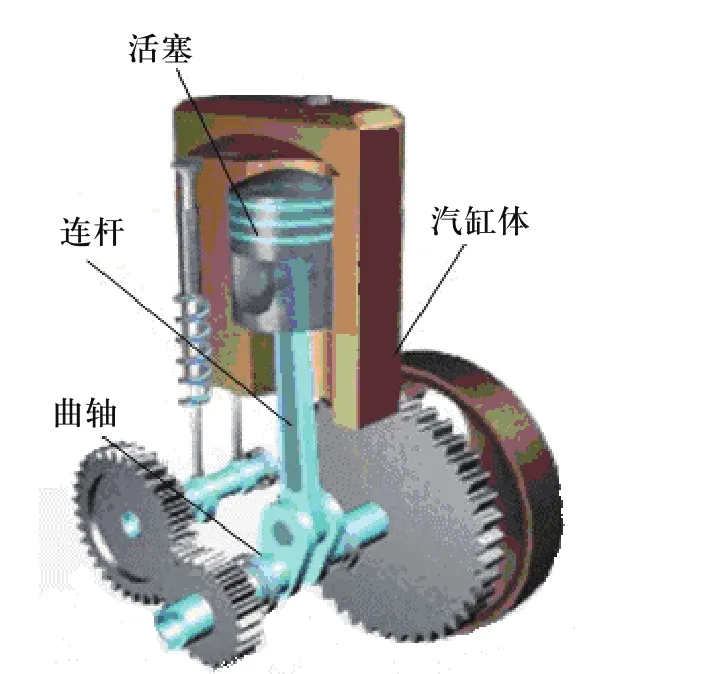
图2 单缸内燃机PRO/E结构图

1 曲柄连杆机构数学模型的建立

曲柄连杆机构向量模型如图3所示。其中滑块的位移r1；曲柄长度r2、转角θ2；连杆长度r3、转角θ3；将曲柄连杆机构的闭环矢量在坐标轴上投影为：

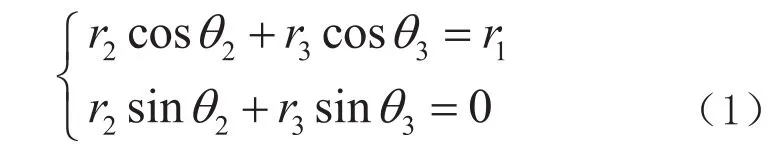
设曲柄长度r2=50mm，连杆长度r3=150mm， 曲柄以角速度ω2=188.5rad/s（n =1800r/min）匀速转动，代入消元后求解得（2）式。

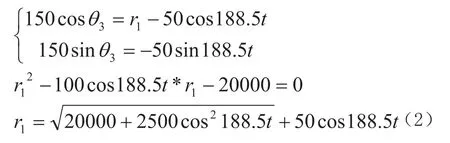
程序：function r=tl0(t)

r=sqrt (20000+2500*cos (188.5*t)^2) + 50*cos(188.5*t)

fplot (’tl0’,[0,0.10])

将（2）式对时间t求导数，得到曲柄连杆机构的速度方程如下：

即可得到滑块位移的仿真曲线图， 如图3所示。同理也可以得到滑块速度仿真曲线图，如图4所示，滑块加速度仿真曲线图，如图5所示，连杆转角仿真曲线图，如图6所示。

图3 曲柄连杆机构向量模型

图4 曲柄连杆机构活塞位移

图5 活塞往复运动速度

2 积分方程初始条件的建立与simulink仿真

Simulink仿真工具的算法主要是数值积分，所以在仿真之前必须为积分器建立适当的初始条件。否则将会导致仿真失败。已知曲柄滑块机构中曲柄长度r2=50mm，连杆r3=150mm， 曲柄以角速度ω2=188.5 rad/s匀速转动，α2= 0。利用速度方程可以计算出t=0起始时刻机构中各构件的位置和速度解分别为：θ2=0，θ3= 0，r1=200mm，ω3=-62.833rad/s。

图6 活塞往复运动加速度

根据积分方程的初始条件和加速度矢量方程，建立Simulink仿真模块如图7所示， 其中以曲柄的角速度ω2和角加速度α2作为输入，各构件瞬时位置、角速度及滑块每个时刻的位移、速度和加速度作为输出，并以向量的形式存储在工作空间simout中。其中仿真模块符号对应关系如下：

图7 Simulink仿真模块

3 各构件的惯性力分析及活塞的受力分析

在对机械进行受力分析时，对于低速机构常由于惯性力小而略去不计，只作静力分析；但对于高速及重型机械，因其惯性力很大（常超过外力），故必须对它作动态静力分析[5]（即将惯性力视为一般外力加在相应构件上，在按静力分析的方法进行分析）。在车用柴油机曲轴连杆机构的运动过程中，发动机的最高转速可达4000～6000r/min，活塞每分钟要要行走几十个行程，线速度非常快，因此引起的惯性力也非常大[6]。活塞顶部在作功行程时，承受着燃气带冲击性的高压力，对于柴油机活塞，其最大值可达6～9 MPa。再加上高速运动而产生的惯性力，使得活塞对气缸壁的侧压力非常大，加速活塞和气缸套的磨损，也容易引起活塞变形。车用柴油机曲轴连杆机构各构件产生的惯性力，不仅与各构件的质量 ，绕过质心轴的转动惯量 ，质心 的加速度 及构件的角加速度 等有关，且与机构的运动形式有关，下面以图5为例来说明各构件的惯性力的计算方法：

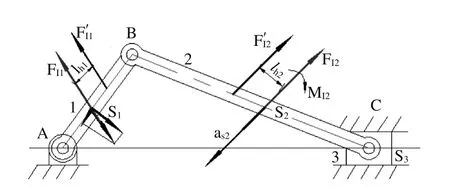
图8 各构件的惯性力

连杆BC由于作平面复合运动且平行于运动平面的对称面，其惯性力系可简化为一个加在质心 S2上的惯性力FI2和一个惯性力偶矩MI2，即FI2＝-m2as2，MI2＝-JS2a2，或简化为总惯性力F′I2＝FI2，而作用线为距质心s2的距离为lh2＝MI2/FI2。

作变速运动的滑块3是作平面移动的构件，所以有一个加在心S2上的惯性力FI3＝-m3as3。而绕定轴转动的曲柄1，若其轴线不通过质心作变速转动时其上作用有惯性力FI1＝-m1as1和一个惯性力偶矩FI1＝-JS1a1，或简化为一个总惯性力F′I1；若其回转轴线通过质心，则只有惯性力偶矩MI1＝ -JS1a1。

内燃机的活塞有承压传力、组成燃烧室的功能，由顶部、头部和裙部三部分组成。其中裙部起导向作用，并承受侧压力，其长短取决于侧压力的大小和活塞直径，具体组成如图9所示。活塞构件常在高温（600～700K）、高压（3～9MPa）、高速(8～12m/s) 、润滑不良的条件下工作，其受力情况十分复杂，主要受力分为气体工作压力、活塞组往复运动惯性力、侧压力及摩擦力，其中惯性力造成发动机周期性附加载荷，引起发动机强烈振动，对柴油机而言相当于活塞重量的300～600倍。

图9 内燃机活塞的结构

现将活塞作为隔离体，图7所示为活塞受力简图，其中，F1(θ)为气体对活塞的作用力；F2(θ)为连杆给活塞的力；F3(θ)为气缸壁对活塞的侧向力；F1(θ)为活塞的惯性力；pg(θ)为气体压力随转角的变化；d为气缸直径； r为曲柄半径；α为连杆转角。由活塞的平衡方程可得

由于一般内燃机所用的曲柄连杆机构中曲柄连杆比λ＜1/3，通过运动学分析，此时活塞运动加速度可以足够精确地简化表示为[7]。在图8中，A点、B点和C点分别表示曲轴中心、曲柄销中心和活塞销中心，θ表示为曲柄转角，α表示为连杆摆角。对式（4）、式（5）联立求解即可得到F1(θ)、F2(θ)、F1(θ) 及单缸内燃机转矩 M (θ)，对于多缸内燃机，总转矩等于不同相位的各缸转矩的叠加。

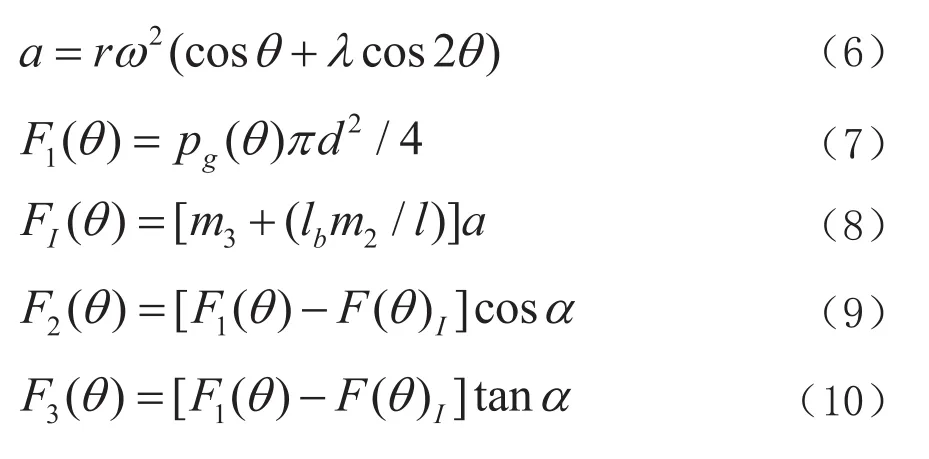
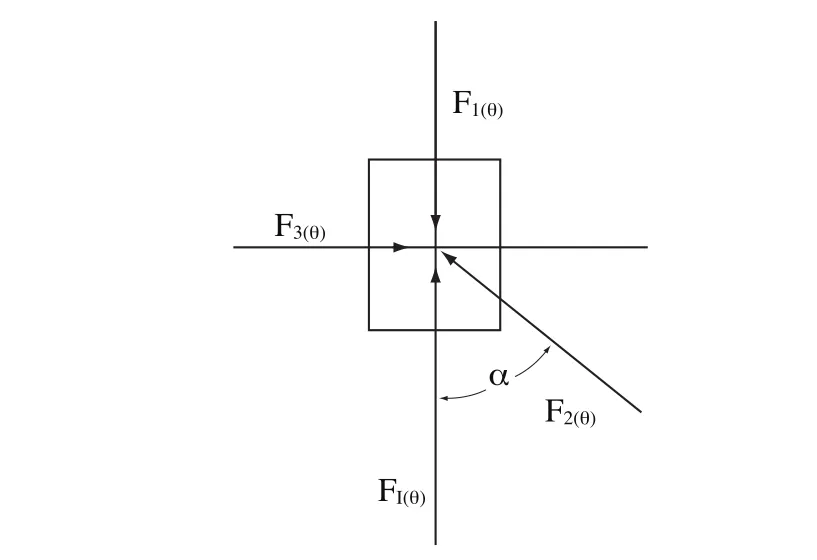
图10 活塞受力简图

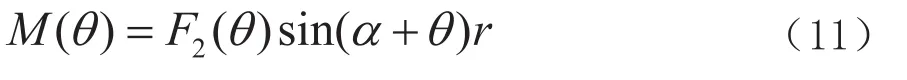
a─活塞运动加速度；

α─表示为连杆摆角；

r─曲柄半径；

θ─曲柄转角；

ω─曲轴旋转角速度；

l─连杆长度；

lb─连杆重心到连杆大头的距离；

m2─连杆质量；

m3─活塞组质量。

图11 内燃机扭矩曲线

4 软件分析在柴油机开发中的应用

本文通过实施正确的软件机构分析方法， 快速而准确地求解复杂多变工况下内燃机连杆机构的运动参数，分析各运动部件的运动规律，从而为后续的多种关键零部件( 如机体、曲轴、连杆、轴承等) 的强度、变形、疲劳和润滑等专门分析提供了正确的输入条件。文章还对曲柄连杆机构的受力状态进行研究，将为内燃机曲柄连杆机构进行优化设计以降低噪声和减少磨损奠定基础；也为曲轴轴承及连杆轴承润滑分析提供前提条件。

[1] 薛定宇,陈阳泉. 基于MATLAB/Simulink的系统仿真技术与应用[M]. 北京： 清华大学出版社,2002.

[2] 孙恒,陈作模. 机械原理. 6版[M]. 北京： 高等教育出版社,2001.

[3] 周进雄,张陵. 机构动态仿真——使用MATLAB和SIMULINK[M]. 西安： 西安交通大学出版社,2002.

[4] 戴旭东,等. 内燃机系统动力学与油膜动力润滑的耦合分析[J]. 西安交通大学学报,2003,37(1)： 55. 58.

[5] 覃文洁. 内燃机曲轴系振动响应的多体系统动力学分析方法[J]. 安全与环境学报,2002,2(2)： 51. 53.

[6] 曹卫彬,梁安波,李江全. 液压挺柱配气机构动力学模型计算的研究[J]. 内燃机工程,2002,23(3)： 58. 60.

[7] 周龙保. 内燃机学 [M]. 北京： 高等教育出版社,2005.