传感器安装偏差对功率流测试误差的影响分析

李朝晖 刘 彦 彭伟才

中国舰船研究设计中心，武汉430064

传感器安装偏差对功率流测试误差的影响分析

李朝晖 刘 彦 彭伟才

中国舰船研究设计中心，武汉430064

为分析传感器安装偏差对功率流测试误差的影响，将安装偏差分解为位置偏差和角度偏差两个部分，并分别基于互功率谱法和波分解法建立传感器安装偏差与功率流测试误差之间的数学模型。仿真分析结果表明：所建立的互功率谱法和波分解法功率流测试误差模型完全一致；位置偏差对功率流的影响由两个传感器位置偏差之差决定，角度偏差对功率流测试误差的影响与频率无关，但始终使得功率流向更小的方向变化，而总误差为两种安装偏差各自产生误差之积。

功率流；互功率谱法；波分解法；测试误差；安装偏差

1 引言

管路系统承担着水、油、蒸汽的输送任务，是现代舰船中不可或缺的重要辅助系统。然而由于其纵横交错、遍及全船，且往往与船体直接相连，因此一旦管路振动出现异常，这种振动和噪声就会通过马脚、穿舱件、空气介质等途径传递至船体进而向外辐射，直接影响舰船的声隐身性能。开展管路功率流测试是分析管路振动传递特性、解决管路振动的重要手段，为此管路功率流测量研究受到国内外学者的重视［1－4］。

充液管路功率流的测试方法主要有波分解法和互功率谱法，其中波分解方法源于管道声学中声强测量的双话筒法，主要特点是通过对测量场的精确测量，利用波理论进行不同轴向模态波的波分解，获得各波的幅值信息，进而进行能量流计算［5］。而互功率谱法则是依据有限差分法，获取沿管壁传递的力与速度的一般表达式，通过力信号与速度信号频域内互功率谱的方法进行能量流频域的计算与分析［6］。这两种方法在梁和管路功率流测试中得到了广泛的应用［7－8］。

由于上述两种测试方法都需要在多个截面布置传感器，传感器安装偏差势必会对测试误差产生一定的影响。然而目前尚缺少这方面的研究，为此本文从理论出发，推导安装偏差与测试误差之间的数学模型，进而研究安装间距偏差、角度偏差对基于这两种测试方法的功率流测试误差的影响规律，为功率流测试方法工程应用提供理论指导。

2 理论建模

纵向波、弯曲波和扭转波为沿管壁传递的三种主要波形，除考虑近场波影响时，弯曲波功率流测试采用4通道模型以外，其它情况均为2通道模型。为便于研究同时又不失一般性，本文仅以2通道模型的波分解法展开讨论。传感器布置方式如图1所示。

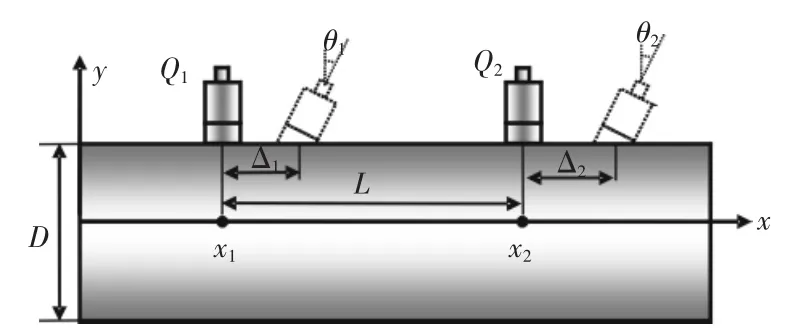
图1 传感器布置原理图Fig.1 Sensors placement

2.1 互功率谱法功率流测试误差模型

如图1所示，将安装偏差分解为位置偏差和角度偏差，并将两个加速度传感器测得的信号分别设为Q1和Q2；x1处因安装产生的位置偏差和角度偏差分别为Δ1和θ1；x2处安装产生的位置偏差和角度偏差分别为Δ2和θ2；沿管壁传递的双向传输波幅值理论上分别为Ap和Am。则传感器测量的信号为：

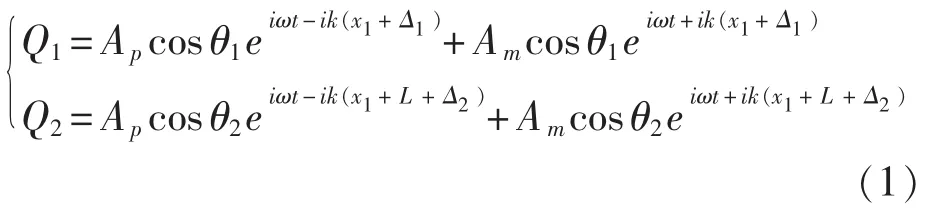
依据互功率谱法，功率流一般表达式为：

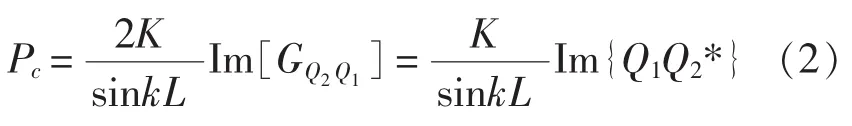
式中，GQ2Q1为两个传感器测得加速度的互谱；K为与波形有关的系数；k为传输波的波数。

将传感器信号Q1和Q2结果带入式（2），整理后得存在偏差条件下的功率流表达式为：

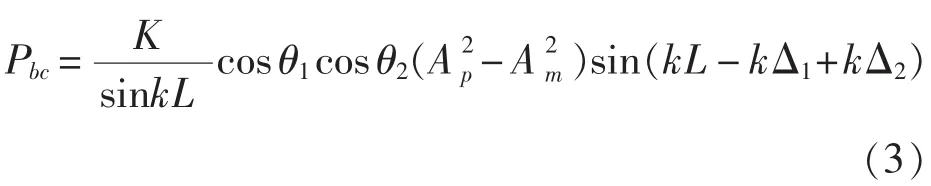
目前，互功率谱法和波分解法均基于梁模型，在该假设前提下，当两个传感器不在同一平面内时，位置偏差以两个传感器所在截面的间距计算，角度偏差以角度与该截面的夹角计算。

2.2 波分解法功率流测试误差模型

由波分解法获取的沿管壁传递的功率流可表示为：

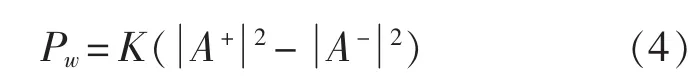
式中，A+，A-为测试所得到的正反两向传输波的幅值。

A+，A-可由传感器测试信号Q1和Q2估算得到：

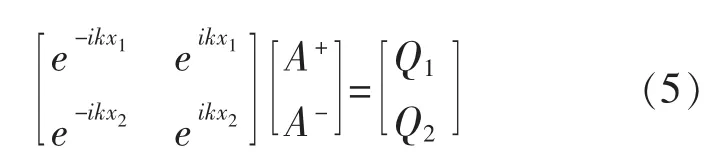
求解方程（5），可得：

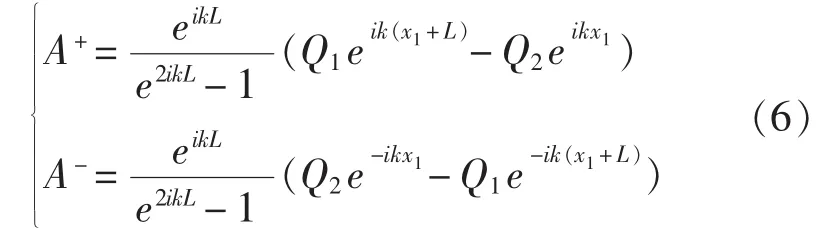
结合式（1）、（3）、（4）和式（6），可得存在安装偏差情况下，波分解法测得的功率流为：

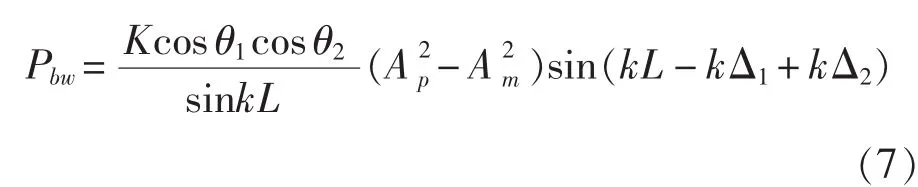
由式（3）和式（7）可见，测试方法虽然不同，但功率流误差模型完全一致。

3 仿真分析

由式（2）和式（6）可知，互功率谱法和波分解法计算功率流的理论值均为：

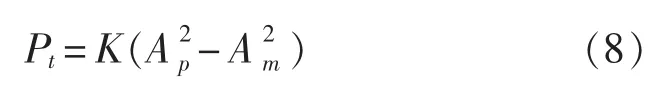
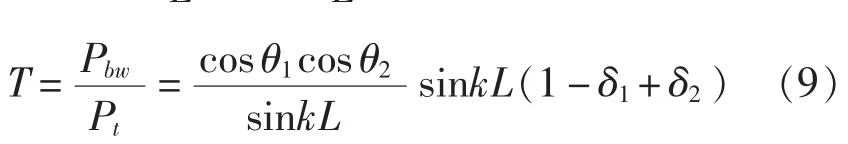
为使分析结果更具一般性，横坐标选用无量纲频率kL，为此需要先确定kL的取值范围。由波分解理论可知，布置间距必须小于最高分析频率对应波长的1/2，即

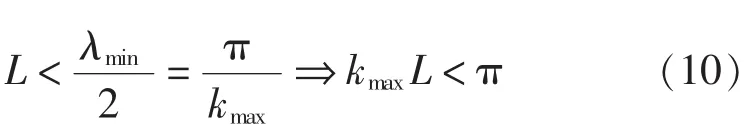
3.1 角度偏差为零时不同位置偏差组合对功率流测试误差的影响

由于理论上波分解法最大可分析无量纲频率无限接近于π，为此分析［0，3］频带内，不同偏差组合对功率流测试误差的影响，如图2所示。由图可见，当δ1－δ2≠0时，在无量纲频率kL大于2以后，测试误差迅速上升，即便是±5%的偏差组合也可能造成约300%的误差。而实际上，由于式（9）中分母为sinkL，致使当kL趋向于π时，功率流误差T趋向于无穷大，除非δ1－δ2＝0使得分子分母中sinkL项相抵消。由于无法确保两端安装位置偏差之差为零，因此实际工程中，一定要确保分析频率kL在2以下，建议选择为π／2，这也与文献［9］建议的最优间距为λmin／4相吻合。

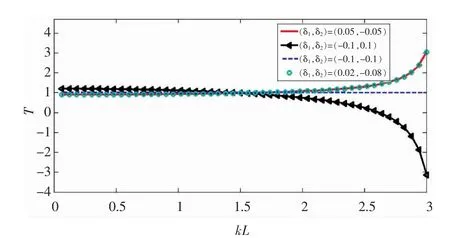
图2 ［0，3］频带内不同位置偏差组合对功率流测试误差的影响Fig.2 Effects on error of power flow by different position deviation groups in［0，3］

在［0，π／2］频率范围内，分析上述四种偏差组合对功率流测试误差的影响，如图3所示。

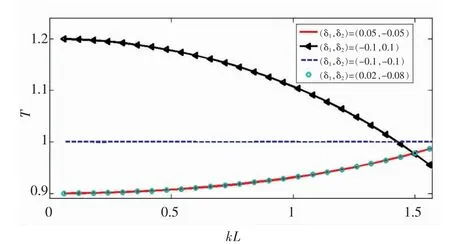
图3 ［0，λ/2］频带内不同位置偏差组合对功率流测试误差的影响Fig.3 Effects on error of power flow by different position deviation groups in［0，λ/2］

由图可见，（0.05，－0.05）偏差组合与（0.02，－0.08）组合因偏差之差相同，对功率流测试误差影响也相同；而（－0.1，－0.1）偏差组合因偏差之差为零，并不产生测试误差。这一规律通过对功率流误差表达式分析也可得出。由式（9）可知，在其他参数不变的前提下，功率流测试误差由两个传感器位置偏差之差决定，即：只要两个传感器位置偏差之差相同，对功率流测试误差的影响就相同；两端位置偏差大小与方向均相同时，将不对功率流测试误差产生影响。

在kL为［0，π／2］分析频段内，±5%的安装误差最高可导致10%的测试误差，而±10%的安装误差可导致20%的测试误差。在工程管路中，弯曲波携带的能量占主导地位，且弯曲波波速随频率变化而变化。对于管径在Ф100 mm以下的管路，在分析频率2 k以上时，对应的布置间距往往在0.2 m以下，而传感器的安装基座往往在2 cm～4 cm。因此，在安装时很可能产生10%甚至20%的位置偏差，必须引起足够的重视。即便对于波速不随频率变化的扭转波和纵向波，在管径Ф100 mm以下、分析频率2 k以上时，对应的布置间距往往在0.5 m以下，因安装产生5%的误差也是很有可能的。此外在分析频段内，功率流测试误差随着频率的升高而降低，因此当存在偏差且δ1－δ2≠0时，功率流低频测试精度往往得不到保证。

3.2 角度偏差对功率流测试误差的影响

由式（9）可知，两传感器角度偏差相互影响，最终体现为小于1的系数cosθ1cosθ2，这意味着角度偏差对功率流测试误差的影响不随频率变化，但始终使得功率流向更小的方向变化。而当存在位置偏差时，角度偏差对功率流的影响如图4所示。由图可见，在kL为［0，π／2］分析频段内，对于δ1－δ2＜0的偏差组合，存在角度偏差可部分抵消位置偏差带来的影响；而对于δ1－δ2＞0的偏差组合，存在角度偏差将加剧对功率测试误差的影响。

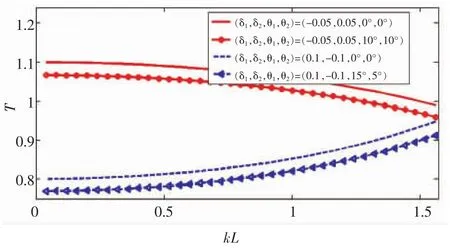
图4 不同位置、角度偏差组合对功率流测试误差的影响Fig.4 Effects on error of power flow by different position and angle deviation groups

在实际工程中，如果能将两端传感器角度偏差均控制在10°以内，则cosθ1cosθ2项产生的误差约为3%，如果能控制在5°以内，对应的误差约为1%。但我们并不能因此忽视角度偏差的影响，因为总误差将以两种安装偏差各自产生误差之积体现，即位置偏差的存在可能会放大角度偏差的影响。经过计算发现，如果在实际工程中严格控制安装偏差，将位置偏差控制在2%以内，角度偏差控制在5°以内，则因安装偏差造成的影响可有效控制在3%以内，这时可忽略安装偏差的影响。

值得注意的是，由式（9）可知，测试偏差T与坐标原点选择（x1）及双向传输波幅值（Ap，Am）没有关系，因此上述结论具有普遍适用性，便于工程应用。

4结论

本文主要研究传感器安装偏差对功率流测试误差的影响。首先分别基于互功率谱法和波分解法建立位置偏差和角度偏差与功率流测试误差之间的数学模型，然后基于该模型研究了位置偏差和角度偏差对功率流的影响规律，结论如下：

1）互功率谱法和波分解法功率流误差模型完全一致，因此，安装偏差影响规律也相同；

2）在仅存在位置偏差条件下，功率流测试误差由两个传感器位置偏差之差决定：只要两个传感器位置偏差之差相同，对功率流测试误差的影响就相同；两端位置偏差大小与方向均相同时，将不对功率流测试误差产生影响。

3）角度偏差对功率流测试误差的影响不随频率变化，但始终使得功率流向更小的方向变化。且对于δ1－δ2＜0的偏差组合，存在角度偏差可部分抵消位置偏差带来的影响；对于δ1－δ2＞0的偏差组合，存在角度偏差将加剧对功率测试误差的影响。

［1］NOBUO T，HIDEAKI S.Cluster power flow control of a distributed－parameter planar structure for generating a vibration－free zone［J］.Smart Materials and Structures，2007，16（1）：47－56.

［2］BRISCOE A R，PINNINGTON R J.Axisymmetric vibrational power measurement in empty and fluid filled pipes［J］.Journal of Sound and Vibration，1996，192（4）：771－791.

［3］WALSH S J，WHITE R G.Measurement of vibrational power transmission in curved beams［J］.Journal of Sound and Vibration，2001，214（2）：157－183.

［4］WOLF K，STOEBER B，SATTEL T.The dynamic coupling and power flow in asymmetric piezoelectric bending actuators［J］.Smart Materials and Structures，2007，16（6）：2015－2025.

［5］张志勇.考虑固液耦合的充液管路系统振动特性及能量流研究［D］.上海：上海交通大学，2000.

［6］VERHEIJ J W.Cross spectral density methods for measuring structure borne power flow on beams and pipes［J］.Journal of Sound and Vibration，1980，70（1）：133－139.

［7］MACE B R，HALKYARD C R，EL－KHATIB H M.Real－time measurement of wave components and intensity in a beam in the presence of a near field ［J］.Journal of Sound and Vibration，2005，286（3）：507－527.

［8］HAMBRIC S A，TAYLOR P D.Comparison of experimental and finite element strucute－brone flexural power measurement for a straight beam［J］.Journal of Sound and Vibration，1994，170（5）：595－605.

［9］HALKYARD C R，MACE B R.Structural intensity in beams-waves，transducer systems and the conditioning problem［J］.Journal of Sound and Vibration，1995，185（2）：279－298.

The Effect of Mounting Deviation on Measuring Error of Power Flow

Li Zhao－hui Liu Yan Peng Wei－cai
China Ship Development and Design Center，Wuhan 430064，China

In order to analyze the influence of mounting deviation on measuring accuracy of power flow，the effect of mounting deviation on error of power flow based both on cross spectral density method and wave decomposition method were developed respectively.The mounting deviation was divided into position deviation and angle deviation.It is shown that the two models are identical.The error caused by position deviation is decided by the difference of position deviation between two transducers，the error caused by the angle deviation does not vary with frequency and always make the power flow smaller than normal，and the total error is the product of the both.

power flow；cross－power spectrum method；wave decomposition method；measuring error；mounting deviation

O329，U664.84

：A

：1673－3185（2011）04－25－04

2011-04-19

国防科工局“十一五”预研项目

李朝晖（1967－），男，硕士，高级工程师。研究方向：噪声振动控制。E-mail：Lzhui701＠126.com

刘 彦（1979－），男，博士，工程师。研究方向：噪声振动控制。E-mail：liuyanhit＠gmail.com

10.3969/j.issn.1673-3185.2011.04.005