非线性热传导方程的Lagrange插值逼近

王天军，贾丽蕊

(河南科技大学数学与统计学院，河南洛阳471003)

0 前言

对线性热传导方程通常用分离变量法求得精确解［1－3］;文献［4］用差分及区域分解法数值求解一维热传导方程;文献［5］用半离散差分格式数值求解一维热传导方程。而这些问题都是Dirichlet边界条件。实际上在科学和工程中经常会遇到Neumann边界条件，比如问题(1)的求解。要求得问题(1)的正确解往往是困难的。因此通常需要求它的数值解。文献［6－7］分别给出了矩形区域上椭圆型方程Neumann边值问题的Legendre谱方法数值求解和误差分析。文献［8］用Fourier变换方法求解波动方程。但遗憾的是问题(1)的数值求解目前尚未见到有关结果。本文将用Lagrange插值多项式作为基函数展开数值解，逼近有界杆上的非线性热传导Neumann边值问题的正确解。利用Lagrange插值多项式的一些性质，可以很容易地求出算法格式中的微分矩阵，为实际计算带来极大的便利，从而达到节省工作量的目的。

1 非线性热传导方程的数值方法

1.1 Lagrange插值多项式的微分矩阵

令LN(x)，1≤x≤1，表示N阶Legendre多项式，令x0=1，xN=1，xm(1≤m≤N1)是L'N(x)=0的根。以xm为节点的lagrange插值多项式为:

设pN(x)=umφm(x)，x∈［1，1］。对pN(x)关于x求一阶导数，并令x=xk，k=0，1，2，…，N得:

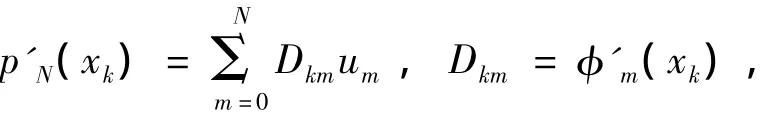
这里D=(Dkm)是(N+1)(N+1)矩阵［910］，且有

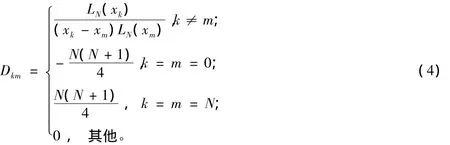
进一步，再对pN(x)求二阶导数，得N

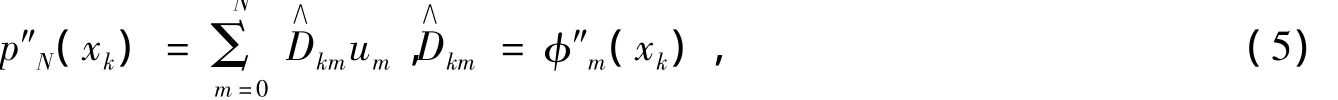
1.2 非线性热传导方程混合问题的算法格式

为利用Legendre-Gauss-Lobatto节点为插值节点求得(1)的数值解，作变换:x=y1，问题(1)化为:

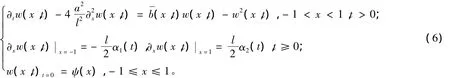
接下来用多项式:wN(x，t)=um(t)φm(x)，x∈［1，1］，逼近(6)的解。将其代入式(6)可得

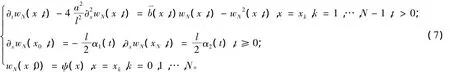
等价地表示为:

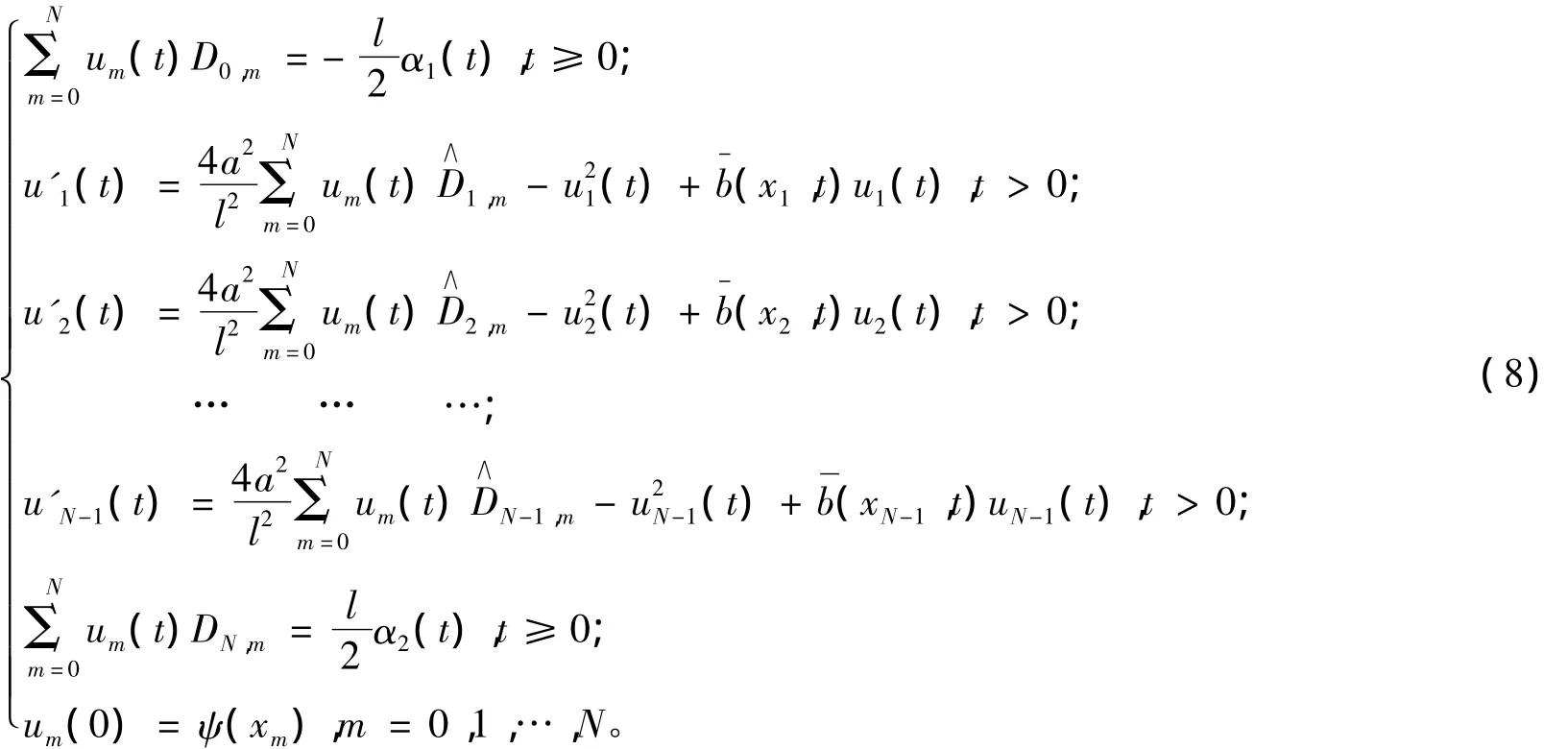
记:

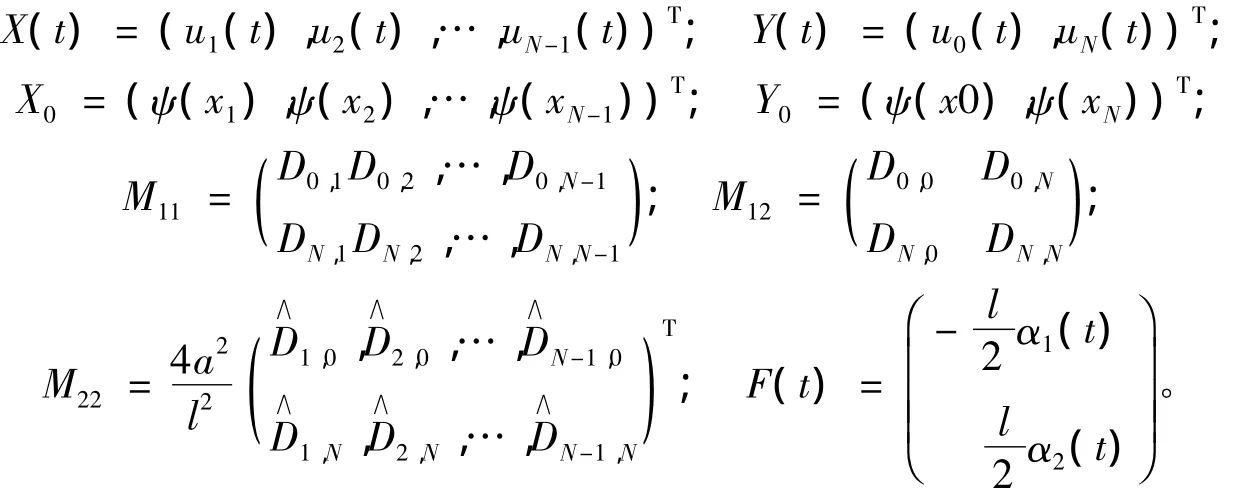
式(8)写为矩阵形式为:

在任意时刻t，由式(9)得到X(t)，Y(t)，其中，M21(t)=(4a2/l2)A+B(t)，矩阵A=(akm)，B(t)= (bkm(t))都是(N1)×(N1)矩阵，其元素分别为:

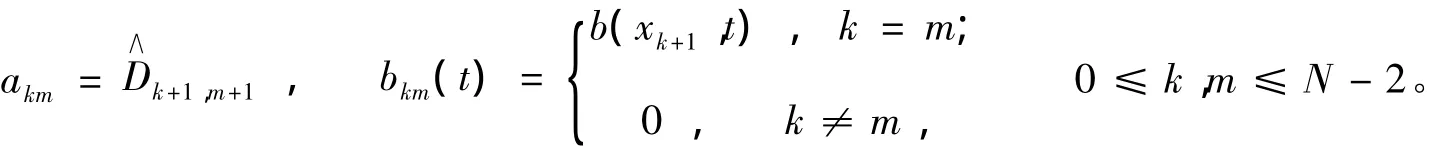
2 数值结果

用格式(9)求解式(6)。在时间方向用步长为τ的Crank-Nicolson格式离散有:

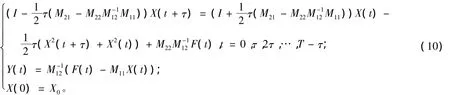
这里I是(N－1)×(N－1)单位矩阵。在式(1)中取a=1，b(x，t)≡1，问题(1)的第一个方程即为著名的Fisher方程:

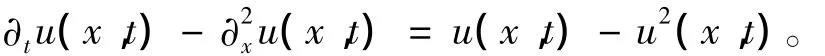
由文献［11］，它的一个正确解为:

在式(6)中取l=2及:

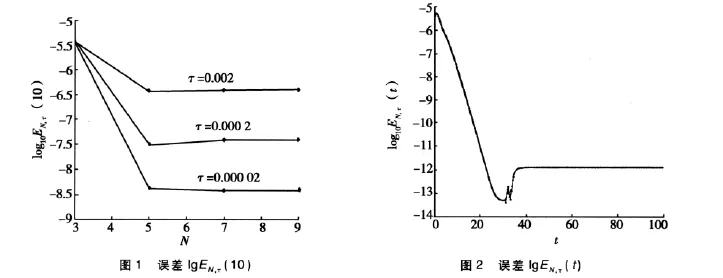
3 结论

本文利用Legendre-Gauss-Lobatto点为插值节点的Lagrange插值多项式为基函数，构造多项式逼近有界杆上的非线性热传导方程Neumann边值问题的正确解。利用Lagrange插值多项式的性质，将偏微分方程转化为求解所构造多项式的系数向量的常微分方程，这样处理简化了非线性项的计算，在实际计算中节省大量工作;特别，解函数的二阶导数所对应的微分矩阵恰好是一阶导数所对应的微分矩阵的乘积，使得算法格式简便，充分体现了所提算法的优势。这里所用方法也可用于有界区域上的其他非线性问题。

［1］ 姜礼尚，陈亚浙，刘西垣，等.数学物理方程讲义［M］.北京:高等教育出版社，2003.

［2］ 谷超豪，李大潜，陈恕行，等.数学物理方程［M］.北京:高等教育出版社，2002.

［3］ Guenther R B，Lee JW.Partial Differential Equations of Mathematical Physics and Integral Equations［M］.Mineola:Dover Publications，2005.

［4］ 王婷.热传导方程的一类有限差分区域分解显－隐算法［J］.山东大学学报:理学版，2006，41(5):20－25.

［6］ Auteri F，Parolini N，Quartapelle L.Essential Imposition of Neumann Condition in Galerkin-Legendre Elliptic Solvers［J］.Comp Phys，2003，185(2):427－444.

［7］ Wang Tianjun，Wang Zhongqing.Error Analysis of Legendre Spectral Method with Essential Imposition of Neumann Boundary［J］.Appl Nume Math，2009，59(10):2444－2451.

［8］ 王天军.一维线性非齐次波动方程解的一个注记［J］.河南科技大学学报:自然科学版，2010，31(2):86－89.

［9］ Alipanah A，Razzaghi M，Dehghan M.The Pseudospectral Legendre Method for a Class of Singular Boundary Value Problems Arising in Physiology［J］.Journal of Vibration and Control，2010，16(1):3－10.

［10］ Shen Jie，Tang Tao.Spectral and High-Order Methods with Applications［M］.Beijing:Science Press，2006.

［11］ 李向正，张卫国，源三领.LS解法和Fisher方程行波系统的定性分析［J］.物理学报，2010，59(2):744－749.