一类静态输出非脆弱控制器的设计

陈文清，沈文杰，宋书中

(1.洛阳理工学院电气工程与自动化系，河南洛阳471003;2.河南科技大学电子信息工程学院，河南洛阳471003)

0 前言

众所周知，基于T-S模型的模糊控制是研究非线性系统比较成功的方法之一，已有很多成果面世［1－3］。对于一些非线性系统当用T-S线性模型不能近似描述时，可以用T-S模糊双线性模型来近似描述［4］。

非脆弱性是控制器设计中的一个重要的因素。非脆弱性表示控制器发生参数摄动时，仍能维持闭环系统稳定的能力。近年来对非脆弱控制器的研究已成为人们感兴趣的课题［5］，上述结果大多是关于状态反馈或基于观测器的状态反馈，关于静态输出反馈控制的结果则很少［6］。输出反馈控制直接利用系统的输出量来设计控制器，且静态输出反馈控制器结构简单，具有良好的应用价值。

本文针对一类模糊双线性系统，在控制器存在加性摄动的情况下，研究了非脆弱静态输出反馈控制问题。根据Lyapunov稳定性理论及线性矩阵不等式(LMI)方法，得到了非脆弱保性能模糊控制器存在的充分条件，并给出了求解控制器的方法。

1 系统的模型描述

考虑一类模糊双线性系统(FBS)，第i条模糊规则可描述如下［1］:

其中，Ri是第 i条模糊规则;s是模糊规则数目;Mji，j=1，2，…，v是模糊集合;ξ(t)=［ξ1(t)，ξ2(t)，...，ξv(t)］T是前提变量;x(t)、u(t)和y(t)分别是状态变量、控制输入和测量输出;Ai，Bi，Ni，Ci是已知的系统矩阵。采用静态输出反馈控制，这里假设ν=q及ξ1(t)=y1(t)，...，ξv(t)=yq(t)。

通过单点模糊化，乘积推理和中心平均反模糊化方法，模糊控制系统的总体模型为:

第i个子系统的输出反馈控制律为:

其中，ρ＞0是待定的标量;Ki∈R1×q是待定的控制器增益;△Fi表示控制器增益的加性摄动，具有结构形式△Fi=HiFi(t)Efi，Hi，Efi是反映不确定性结构的常数矩阵，Fi(t)是一个未知时变矩阵，其元素Lebesgue可测且对任意的t满足:F(t)Fi(t)≤I。

则整个系统的状态反馈控制律可表示为:

在控制律(4)的作用下，整个闭环系统的方程可表示为:

2 主要结论

引理1［7］设M，N是适合维数的实矩阵，则对于标量ε＞0，有MTN+NTM≤εMTM+ε1NTN成立。

引理2［8］给定适当维数的矩阵G，E和对称矩阵S，不等式S+GFE+ETFTGT＜0对所有满足FT(t)F(t)≤I的矩阵F(t)成立，当且仅当存在一个常数ε＞0，使得S+εGGT+ε1ETE＜0。

定理1 对于给定的常数ρ＞0和ε1＞0，如果存在着矩阵Z＞0和矩阵Ki，i=1，2，…，s满足不等式(6)，则闭环系统(5)是渐近稳定的，控制律(4)是一个非脆弱控制律。

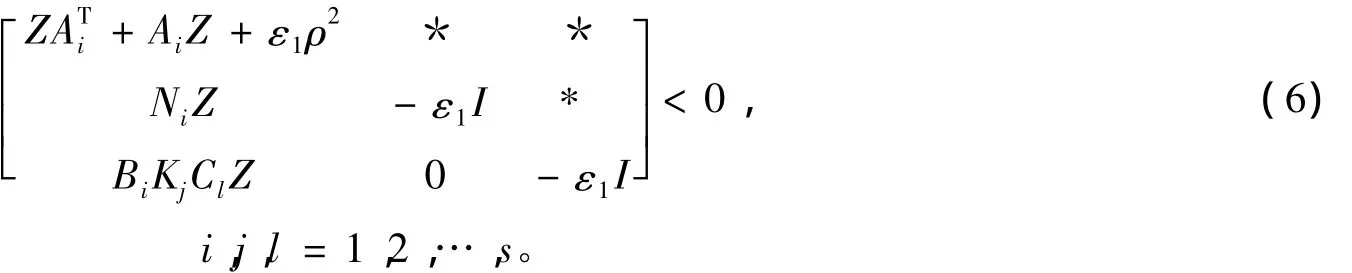
证明 选取如下Lyapunov函数:

其中，P=Z－1是待求的正定对称矩阵。

沿着系统(5)的轨线，对V(t)求导，可得到:

由引理1可知:

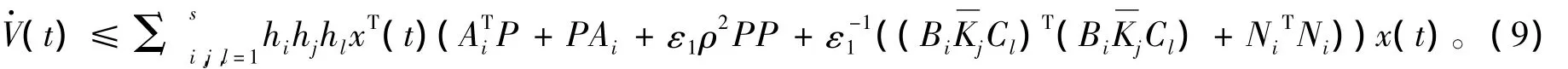
对定理1中的式(6)同时左右乘diag{P，I，I}，并由Schur补定理可得到:V(t)＜0。由此可知闭环系统(5)是渐近稳定的，且控制律(4)是一个非脆弱控制律。

定理2 对于常数ρ＞0和ε1＞0，ε2＞0，0＜a＜ε1，如果存在着矩阵Z＞0和矩阵Ki，i=1，2，…，s满足LMI(10)，则系统(5)是稳定，控制律(4)是一个输出非脆弱保性能控制律。

证明 由Schur补定理，式(10)可等价于:

由引理2可知，式(11)可推导出:

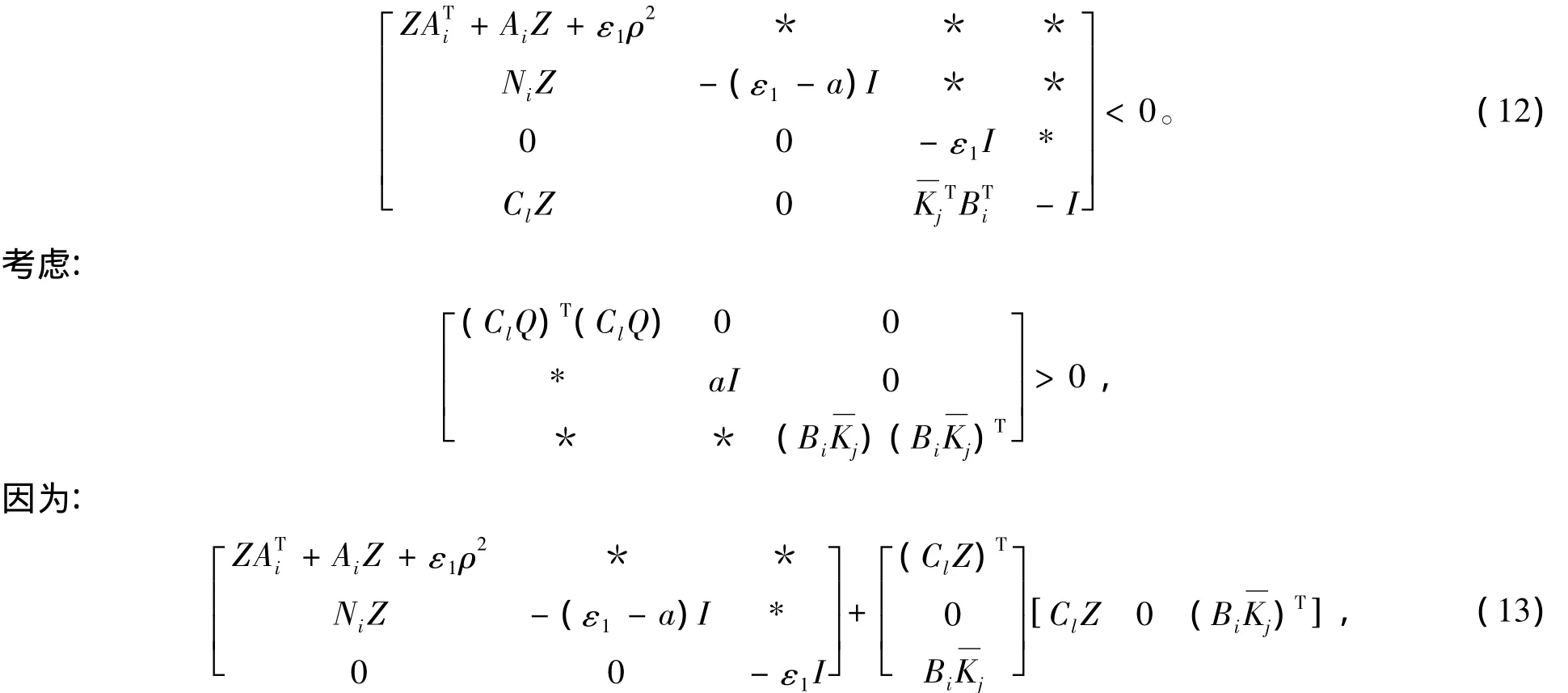
由Schur补定理可知，式(12)可等价于:

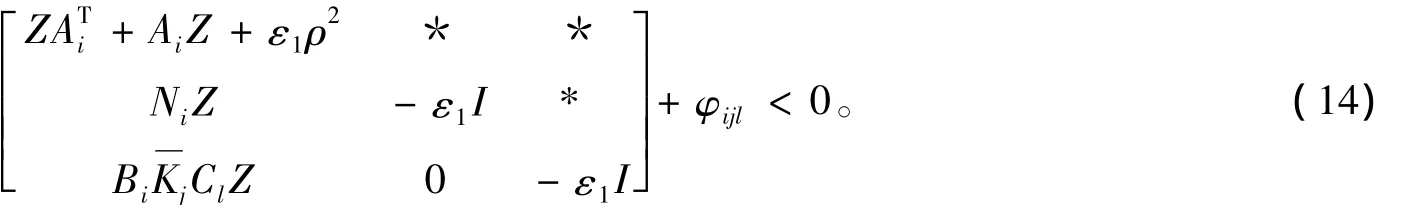
从而可知定理1中式(6)成立，那么可知闭环系统是渐近稳定的。

3 算例分析

考虑一个模糊双线性系统:

系统方程为:

考虑控制器的加性摄动△F(t)为:H1=H2=0.1，Ef1=0.01，Ef2=0.01，F(t)=sin t。选取隶属度函数为μM1(y1)=，μM2(y1)=1μM1(y1)。选取ρ=0.87，ε1=10，ε2=0.11，a= 0.01，根据定理2，通过Matlab求解相应的LMI，可以得到:K1=［0.101 4］，K2=［0.344 2］。

选取初始值为［－2.8 1.6］T，MATLAB仿真可得到系统的状态响应曲线和控制响应曲线(见图1和图2)。从图1和图2中可以看出:非脆弱控制器在受到干扰时可以保证闭环系统的渐近稳定。

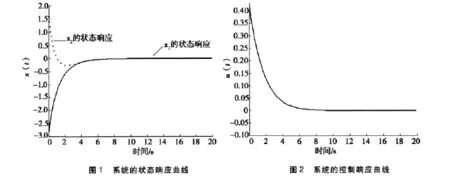
4 结论

本文研究了一类模糊双线性系统的静态输出反馈非脆弱控制问题。当状态变量不可观测时，采用静态输出反馈进行控制。利用并行分布补偿算法，结合线性矩阵不等式技术，得出了控制器增益具有加性摄动时的模糊反馈控制器的设计方法，而且控制器增益可由LMI求出。由实例仿真验证了本文所提方法的有效性。

［1］ Qiu Jianbin，Feng Gang，Yang Jie.A New Design of Delay-Dependent Robust H∞Filtering for Discrete-Time T-S Fuzzy Systems With Time-Varying Delay［J］.IEEE Trans Fuzzy Syst，2009，17(5):1044－1058.

［2］ 尹云飞.数据挖掘与人工智能技术［J］.河南科技大学学报:自然科学版，2004，25(3):44－47.

［3］ 徐巍，张业鹏.基于遗传算法的模糊神经网络控制器在虚拟仪器中的实现［J］.河南科技大学学报:自然科学版，2005，26(3):40－43.

［4］ Li T H S，Tsai SH.T-S Fuzzy Bilinear Model and Fuzzy Controller Design for a Class of Nonlinear Systems［J］.IEEE Trans Fuzzy Syst，2007，15(3):494－505.

［5］ Zhang B Y，Zhou S S，Li T.A New Approach to Robust and Non-fragile H∞Control for Uncertain Fuzzy Systems［J］.Information Sciences 2007，177:5118－5133.

［6］ Kau SW，Lee H J，Yang CM，etal.Robust H∞Fuzzy Static Output Feedback Control of T-SFuzzy Systemswith Parametric Uncertainties［J］.Fuzzy Sets and Syst，2007，158:135－146.

［7］ Wang R J，Lin WW，WangW J.Stabilizability of Linear Quadratic State Feedback for Uncertain Fuzzy Time-delay Systems［J］.IEEE Trans SystMan Cybe，2004，34(2):1288－1292.

［8］ Ho W C，Niu Y.Robust Fuzzy Design for Nonlinear Uncertain Stochastic Systems via Sliding-Mode Control［J］.IEEE Trans Fuzzy Syst，2007，15(3):350－358.