风力机叶片翼型的结冰数值模拟研究
朱程香,王 珑,孙志国,付 斌,朱春玲
(南京航空航天大学航空宇航学院,江苏 南京 210016)
0 引言
风力机是将自然界的风能转换成机械能并获得电能的装置。风力机通常工作在野外,工作环境包括了寒冷地区,海边以及山区等,经常遇到环境温度较低,含湿量较大,空气中含有过冷液态水滴,冰雨或者雪[1]的天气条件,此时风力机面临着结冰的危险。
风力机结冰改变了风力机叶片的气动外形,导致风力机叶片翼型的升力减小,阻力增大,失速攻角减小;风力机叶片不同部位结冰量不同,增加了部件的不平衡性和疲劳程度;风力机叶片表面冰层脱落会损坏其他部件[2]。因此研究风力机叶片翼型的结冰增长过程,预测不同条件下的结冰冰形,可为风力机防除冰系统提供数据支持,降低风力机在结冰条件下发生故障的可能性。
不同环境和气象条件下的结冰冰形不同,主要包括霜冰和明冰两种,霜冰的结冰温度较低,一般小于-10℃,冰形轮廓曲线较光滑;明冰结冰温度较高,一般在0℃ ~-10℃之间,外形曲线较不规则,经常出现角状或棱状。Homola[3](2009 年),Virk[4](2010 年)等人研究表明,霜冰对大型风力机的影响较小。Ducan[5](2008)等人研究表明较霜冰而言,风力机表面形成明冰时,会引起更严重的危害。迄今为止,国内外对于风力机霜冰的数值模拟研究较多,技术也比较成熟,但是对于风力机明冰的数值模拟以及明冰对风力机叶片性能影响的研究相对较少。
本文重点研究了风力机结冰数值模拟方法,计算了不同环境条件和气象条件下风力机叶片翼型表面的结冰冰形,同时模拟了结冰后翼型周围的空气流场,计算了结冰后翼型的气动特性,并与干净翼型的气动特性进行了对比,分析了结冰对于翼型气动性能的影响,各环境参数和气象参数对翼型表面的结冰冰形,以及不同的结冰冰形对翼型气动特性的影响。
1 结冰数值模拟方法
1.1 流场计算
基于质量、动量、能量守恒原理,对控制容积列出不可压缩雷诺平均Navier-Stoke方程[6],为使方程封闭,引入两方程的剪切力输运k-ωSST湍流模型[7],该湍流模型具有良好的稳定性和收敛性。采用有限体积法求解控制方程,空间离散采用中心差分格式,时间离散采用四步Runge-Kutta格式,为了使离散格式稳定,加入了人工耗散项[8],为加速程序收敛,采用了当地时间步长和残值光顺技术。
计算区域包括叶片周围的旋转区域和外层的静止区域。外层入口边界距离叶片10L(L为叶片展长),出口边界距离叶片11L,上下边界距离距离翼型10L,入口边界给定来流的压力,速度,温度和湍流强度,出口边界给定出口静压。
1.2 水滴运动轨迹计算
以单颗水滴为研究对象,根据牛顿力学第二定律建立水滴轨迹运动微分方程[9-10]:

其中,vx、vy表示气流无因次速度,ux、uy表示水滴无因次速度可用下列公式计算[11]:

水滴相对运动雷诺数Rew可用水滴雷诺数Rew0、气流速度和水滴速度获得。
无因次参数K为水滴的运动惯性参数,表示为:

其中,d表示水滴直径,μ表示空气粘度,V0表示来流速度,ρw表示水滴密度,L表示部件几何特征长度。
基于三维风力机流场的计算结果,截取二维截面的流场数据,获得二维截面上网格各个节点上流场参数。但是,在求解水滴运动微分方程时,需要水滴所在位置的空气流动速度,而这个位置不一定是网格节点,因此必须利用已知的网格节点速度求解流场中任意一点的空气流速,为计算水滴运动速度提供前提条件。方法为:①判断水滴所处的网格单元;②根据水滴所处网格四个节点上的气流速度,插值得到该点处的空气流速。
判断水滴所处网格单元的方法如下:假设单元格由1,2,3,4 四个节点构成,其坐标分别为(x1,y1),(x2,y2),(x3,y3),(x4,y4)。水滴在某个时间步长后所处的位置为0,其坐标为(x0,y0)。当0(x0,y0)在四边形内时,点0,1,2构成逆时针回路且点0,3,4也构成逆时针回路;而当0(x0,y0)在四边形外时,点 0,1,2 构成逆时针回路但是点0,3,4却构成了顺时针回路。由数学知识可知,若0(x0,y0)在四边形1234内,则有
否则点0(x0,y0)在四边形1234外。
判断出水滴所处的网格单元后,读取此网格四个节点的流场速度,并用面积加权求和法计算水滴所在位置的气流速度。
水滴撞击特性之一局部水收集系数为微元上收集到的水滴质量与最大可能收集量之比,可根据拉格朗日法获得的水滴运动轨迹求得[12]:

其中dY0表示与微元表面上、下两条相交轨迹的水滴原始坐标之差;dS表示微元上下界限间的表面长度。
考虑水滴多尺寸分布时,为了计算部件表面局部水收集系数,首先需要计算出每种水滴直径对应的水滴运动轨迹及其在部件表面的局部水收集系数,然后根据公式[10]:

求得。其中ni表示第i种直径的水滴的体积分数;βi表示第i种直径的水滴对应的局部水收集系数。
本文进行计算时水滴直径均采用Langmuir D分布进行,但是为了区别各种直径大小和表示方便,在进行分析时仅明确了Langmuir D分布对应的MVD值。
1.3 结冰增长模拟
采用Messinger控制容积思想,在结冰部件表面,由附面层外边界,部件表面,以及垂直于表面的展向侧面围成的控制体为研究对象,进入和流出控制体的各质量流量达到稳定后有如下的质量平衡方程(6)和能量平衡方程(7)[13-14]:

式中:˙m表示质流密度;下标clt表示收集到的水项,in表示上游溢流水项,evp表示水蒸气项,out表示溢流水项,ice表示冰项。
引入冻结系数frz,即冻结了的水的质量与进入的水总质量之比[15]:

联立上式及水滴的质量守恒方程(6)和能量守恒方程(7),并将各项热流的表达式代入可得冻结系数的表达式:
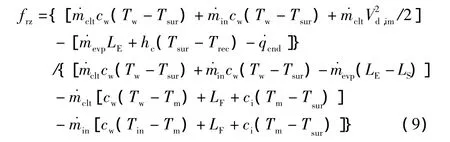
Tw,Tin,Tsur分别是来流水温、入流水温、表面温度;Tm表示平衡温度,一般直接取为冰点;Vd,im表示水滴撞击在表面时的速度,c表示定压比热容;下标i、w分别指示冰和水的参数。LF为冰的融解潜热,LE为水的蒸发潜热。
对于非驻点控制容积方程(9)中有3个未知数,分别是冻结系数frz,表面温度Tsur,上游流入当前控制体的水量min,但驻点控制容积中无入流水,即min(0)=0。又因物理上有约束条件:0≤frz≤1,且液态水的流动主要受气流驱动影响,沿表面向后缘流动[15]。故可以从驻点控制容积开始依次向后分别求解上、下表面所有控制容积中的质量和能量守恒方程,从而得到各个控制容积中的冻结系数机翼结冰速率。
结冰高度:

其中,△s(i):控制体下界面的面积;ρice,(i):控制体中所结冰层的密度。
1.4 多时间步长结冰数值模拟
部件表面结冰是环境参数,气象参数,部件几何参数以及时间的复杂动态函数。结冰后,部件的几何外形发生变化,因此需要重构部件几何,并生成网格进行流场、水滴撞击特性和部件表面局部换热系数,结冰增长及结冰冰形的计算。
此过程中部件表面结冰后的模型更新和网格重构是非常重要的环节之一。以机翼为例,由于机翼表面结冰发生在机翼前缘,因此为了节省计算资源,可以保持机翼其它区域网格不变,只更新前缘结冰区域及附近的网格。
由于风力机叶片翼型结冰缺乏实验数据,因此本文以NACA0012翼型为研究对象,采用本文计算方法模拟了翼型表面的霜冰和明冰,并与相同条件下的冰风洞试验数据进行了对比,如图1和图2所示。可以看出,采用本文计算方法模拟的冰形与冰风洞试验数据吻合得很好,由此说明了本文计算方法的正确性。


2 计算结果和分析
本文以某商用风力机叶片翼型(NACA63618)为研究对象,由于风力机叶片上距离翼根85% ~100%之间的区域对于风力发电而言最重要,因此本文研究的截面位于风力机叶片上距离翼根88%的位置[2]。
本文采用上节所述方法计算了如表1所示的各种环境条件和气象条件下,翼型表面的结冰增长率和结冰冰形,并分析了不同结冰冰形对翼型气动特性的影响。

表1 计算状态参数表Table 1 Parameters for caculation
2.1 不同环境温度下的计算结果分析
图3显示了环境温度T分别为-2.5℃,-7.5℃,-15℃,MVD 为20μm,LWC 为 0.5 g/m3时翼型表面的结冰冰形,可以看出,环境温度为 -2.5℃,-7.5℃时,翼型表面形成明冰,环境温度为-15℃时,翼型表面形成霜冰。这是因为环境温度较低时,撞击到翼型表面的水滴全部立即冻结,水滴之间夹杂的空气没有机会排出,形成透明度差,表面粗糙的霜冰;环境温度较高时,撞击到翼型表面的水滴未能全部迅速冻结,有一部分水滴保持液态形成水膜向翼型后方流散并在翼型后方冻结,从而在翼型前缘形成凹槽,后方形成角状明冰。
图4为干净翼型周围,以及形成如图3所示的三种冰形后,攻角为15°时翼型周围的空气流线分布。可以看出,未结冰前,翼型尾缘发生了分离,但是分离区非常小,结冰后,翼型尾缘分离区非常明显,并且翼型表面形成明冰(T=-2.5℃和T=-7.5℃)时的尾缘分离区较翼型表面形成霜冰时的尾缘分离区大。分离区的不同造成了翼型气动特性的不同,图5显示了翼型表面的升力系数曲线,图6显示了翼型表面的升阻比随攻角的变化曲线,可以看出T=-7.5℃时升力最小,升阻比最小,较干净翼型而言,升阻比最大降低60%。

图3 不同温度条件下的冰形Fig.3 Ice shape calculated with various ambient temperature



2.2 不同水滴直径条件下的计算结果分析
图7显示了平均容积直径MVD分别为15μm,20μm,25μm,环境温度为 -2.5℃,LWC 为 0.5 g/m3时翼型表面的结冰冰形,可以看出,随着MVD的增大,结冰量逐渐最大,但是增加幅度较小。


图8 为攻角为 15°时 MVD 分别为 15μm,20μm,25μm时结冰翼型周围的空气流线分布。可以看出,结冰后,翼型尾缘出现较明显的分离区,并且MVD为20μm和25μm时的尾缘分离区较大。分离区的不同造成了翼型气动特性的不同,图9显示了翼型表面的升力系数曲线,图10显示了翼型表面的升阻比随攻角的变化曲线,可以看出MVD=20μm时升力最小,升阻比最小。


2.3 不同液态水含量条件下的计算结果分析
图11显示了液态水含量LWC分别为0.1g/m3,0.5 g/m3,0.75g/m3,环境温度为 - 2.5℃,MVD 为 20μm 时翼型表面的结冰冰形,可以看出,结冰量随着LWC的增大而增大,这是因为LWC增大后,翼型表面收集到的水量增大,结冰量增加。

图11 不同液态水含量条件下的冰形Fig.11 Ice shape calculated with various LWC
图12为攻角为15°时形成如图11所示的三种冰形后翼型周围的空气流线分布。可以看出,结冰后,翼型尾缘出现较明显的分离区,LWC为0.75 g/m3时的尾缘分离区最大。分离区的不同造成了翼型气动特性的不同,图13显示了翼型表面的升力系数曲线,图14显示了翼型表面的升阻比随攻角的变化曲线,可以看出LWC=0.75 g/m3时升力最小,升阻比最小,较干净翼型而言,升阻比最大降低61%。



图14 干净翼型及结冰后翼型升阻比曲线Fig.14 Lift/drag performance curves for plain and iced airfoils
3 结论
本文研究了风力机叶片翼型的结冰数值模拟方法,计算了不同环境和气象条件下翼型表面的结冰冰形,并分析了不同结冰冰形对翼型气动特性的影响,得出以下结论:
(1)翼型表面结冰会造成翼型周围气流提前发生分离,翼型升力降低,阻力增大,升阻比减小,本文计算条件下,升阻比最大降低幅度达到了61%左右。
(2)环境温度较低时,翼型表面形成霜冰,环境温度较高时,翼型表面形成明冰,且明冰对翼型气动特性影响较霜冰大。
(3)气象参数水滴直径和液态水含量增大,结冰量增大,翼型周围气流分离区增大,升阻比减小。
[1]FORTIN G and PERRON J.Wind turbine icing and de-icing[R].AIAA 2009-274,2009.
[2]MATTHEW C HOMOLA,MUHAMMAD S VIRK,TOMAS WALLENIUS,etc.Effect of atmospheric temperature and droplet size variation on ice accretion of wind turbine blades[J].Wind Energy,2010,98(12):724-729.
[3]HOMOLA M C,WALLENIUS T,MAKKONEN L,NICKLASSON P,SUNDSBøP A.The relationship between chord length and rime icing on wind turbines[J].Wind Energy,2010,13(7):627-632.
[4]VIRK M S,HOMOLA M C,NICKLASSON P J.Effect of rime ice accretion on aerodynamic characteristics of wind turbine blade profiles[J].Wind Engineering ,2010,34(2):207-218.
[5]DUNCAN T,LEBLANC M,MORGAN C,LANDBERG L.Understanding icing losses and risk of ice throw at operating wind farms[J].Winterwind,2008,31(2):263 -270.
[6]CHUNG,JAMES,REEHORST,ANDREW,CHOO,YUNG,POTAPCZUK,MARK and SLATER,JOHN.Navier-Stokes analysis of flowfield characteristics of an ice-contaminated aircraft wing[R].AIAA -1999-0375.
[7]SHIM,JEONGHWAN,CHUNG,JUNE,and LEE,KI D.A comparison of turbulence modeling in flow analysis of iced airfoils[R].AIAA 2000-3920,January 2000.
[8]RICHARD E KREEGER,WILLIAM B WRIGHT.The influence of viscous effects on ice accretion prediction and airfoil performance predictions[R].AIAA-2005-1373.
[9]GARY A RUFF and BRIAN M BERKOWITZ.Users manual for the NASA Lewis ice accretion prediction code(LEWICE)[R].NASA CR -185129,May 1990.
[10]WILLIAM B WRIGHT.User manual for the NASA Glenn ice accretion code LEWICE version2.2.2[R].NASA CR -2002-211793,August2002.
[11]WELLS S L and BRAGG M B.A computational method for calculating droplet trajectories including the effects of wind tunnel walls[R].AIAA -92 -0642
[12]STEVEN C CARUSO.Lewice droplet trajectory calculations on a parallel computer[R].AIAA 93 -0172.
[13]TIM G MYERS.Extension to the messinger model for aircraft icing[J].AIAA Journal2001,39(2):211 -218.
[14]TIM G MYERS and CHRIS P THOMPSON.Modeling the flow of water on aircraft in icing gonditions[J].AIAA Journal,1998,36(6):1010 -1013.
[15]GUY FORTIN,ADRIAN ILINCA,JEAN-LOUIS LAFORTE,VINCENZO BRANDI.Prediciton of 2D airfoil ice accretion by bisection method and by rivulets and beads moddeling[R].AIAA-2003-1076.

