浅谈GPS-PTK作业中区域椭球的建立
祁敏敏
(浙江省河海测绘院,浙江 杭州 310008)
1 问题的提出
GPS卫星定位技术的迅速发展,已经给测绘领域带来了飞跃性的变革。GPS定位技术与其他常规测量技术相比有着明显的优势和特点,它用途广、自动化程度高、观测速度快、定位精度高、经济效益好。利用GPS建立城市及工程控制网已经得到广泛的应用。RTK(Real Time Kinematic)技术是GPS测量技术和数据传输结合而成的实时定位技术,主要由基准站和流动站两部分组成。随着RTK技术的迅速发展,实时定位已经得到广泛的应用,如何利用RTK技术直接测定平面坐标和高程的方法有很多,由于RTK采用基准点的精确坐标进行的实时观测,没有多余观测,无须平差,因此直接测定平面坐标和高程的关键在于由RTK观测的WGS-84坐标到平面坐标和高程数据之间的转换。
首先利用RTK观测的基线向量,计算出RTK流动站在WGS-84参心坐标系中的三维坐标,然后由椭球变换所得的参数和在平面转换所得的高斯参数,将其直接计算转换到地方独立坐标系,得到平面坐标。在上述过程中其实是由一个吻合于投影面的区域性椭球面作为过渡,也就是先将WGS-84椭球转换为E3椭球,再把E3椭球基于一些GPS水准联测点作椭球定向定位的调整[1],然后再次继续调整E3椭球元素,使区域椭球面最优吻合于投影面。这是与通常须借助于二维国家控制点来求取转换参数的方法是截然不同。
2 确定区域椭球面的方法
区域性椭球面的确定有2种方法:单点法、多点法。它们可通过改动椭球元素,或是改变椭球的定向和定位,来使区域性椭球面与投影面在单点上或是在多点上相吻合,下面对本文所涉及的一些方法予以介绍。
3 由单点法确定E3椭球面
由单点法确定E3椭球面见图1。

图1 由单点法确定E3椭球面图
设P0为GPS控制网中的一个基准点,其正常高为h0,在已知椭球面上的大地高为H0,投影面的正常高为 △h,则P0相对于投影面的正常高为h0-△h。同时设位置基准点在已知椭球面上的大地坐标为(B0,L0,H0)。
首先将位置基准点的大地高变为h0-△h,以维持 P0点上椭球面法线方向及经纬度B0,L0不变,再采用同时改变椭球长半径和偏心率的方法,以保证P0点的三维坐标不变,从而使椭球中心不产生移动,由参考文献[2]证得E3椭球偏心率和长半径a3由下式计算得出:
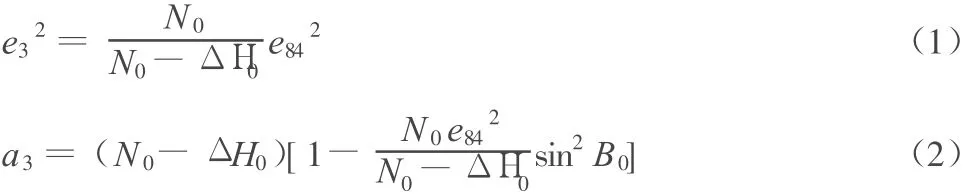
其中 Δ H0=h0-Δ h-H0

4 对E3椭球进行定向定位
由上述方法所得的E3椭球面,是利用单个位置基准点上的已知椭球面和投影面之间的垂向距离△H0数据,同时改变已知椭球的长半径和偏心率,从而使所设置的区域性椭球面与投影面能在基准点处相吻合,但两个面之间仍然有一定偏离,如图1所示。随着测区面积的增大,这种偏离的程度会越来越大,而这种偏差的主要原因是区域性椭球面与投影面之间存在倾斜 (即位置基准点上的垂线偏差),这就会造成在高斯平面上GPS网与地面网间不可忽略的尺度偏差。因此对于大面积测区,应采用多点法对E3椭球定向定位代替单点法来确定区域性椭球面。多点法确定区域性椭球面需要获得GPS点的正常高,而GPS网测设过程中原本就须对部分GPS点进行水准联测,这也不仅使得多点确定区域性椭球面成为可能,同时也提供了数据支持。
由E3椭球面的确定方法可知,所得到的E3椭球面已在位置基准点P0处与投影面重合,除了椭球元素与WGS-84椭球不同外,椭球的定向定位以及 P0点上椭球法线均相同,为使区域椭球面与投影面在整个测区内更好的吻合,首先应把这两个面之间的倾斜减少甚至消除。
4.1 E3椭球面的垂线偏差与站心赤道坐标系中的欧拉角的关系式
在P0点上,E3椭球面的法线方向与垂线方向并不一致,其夹角即为垂线偏差u,即E3椭球面相对于投影面的倾斜角,它可以分解为子午分量 ξ和卯酉分量η,若采用以基准点P0为坐标原点的站心左手地平直角坐标系,以该点处的
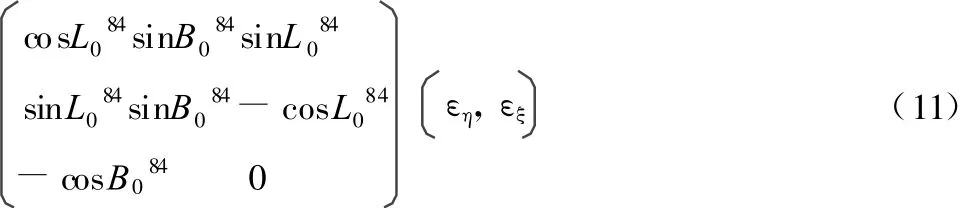
E3椭球法线方向为z轴,x轴指向P0的子午线方向,以北为正,y轴也位于该点切平面上,东向为正。在地平直角坐标系中,若以P0点为旋转中心,先后饶y轴旋转εξ,以及饶x轴旋转εη,即可将z轴由E3椭球法线方向旋转到垂线方向,对于左手坐标系而言:
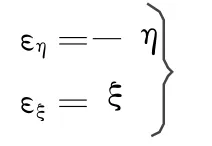
两次旋转后,得到以垂线为z轴的站心地平直角坐标系中任一点Pj的坐标为:
转换前所相应的站心赤道坐标系也获得了类似的转换,起旋转角为:εX,εY,εZ。

由文献[1]可知,2类旋转角之间的关系式为:
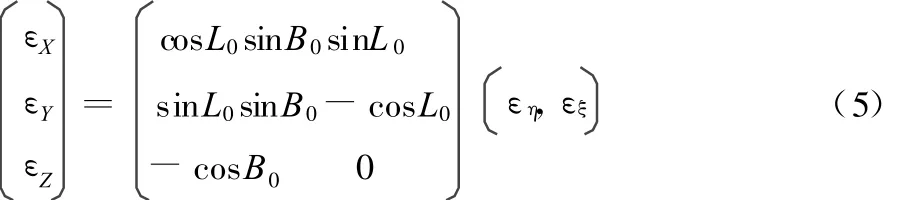
4.2 旋转中心三维坐标不变的椭球中心的平移公式
根据区域性椭球面的需要,要求空间大地直角坐标系(X′,Y′,Z′)的各坐标轴仍平行于旋转后的站心赤道坐标系的各坐标轴,且要求旋转中心 P0的三维坐标仍保持不变,因此就必须使椭球中心作平行移动,于是可将任一点的空间直角坐标变换式写成:

上式(6)中,(δX,δY,δZ)T为坐标原点即椭球中心的平移向量,为使旋转变换后P0点的三维直角坐标(X0,Y0,Z0)保持不变,由(6)式可得椭球中心的平移量为:

4.3 旋转变换后的大地坐标变动量
由文献[1]可证得大地高变动量dH′J与垂线分量之间的关系式为:
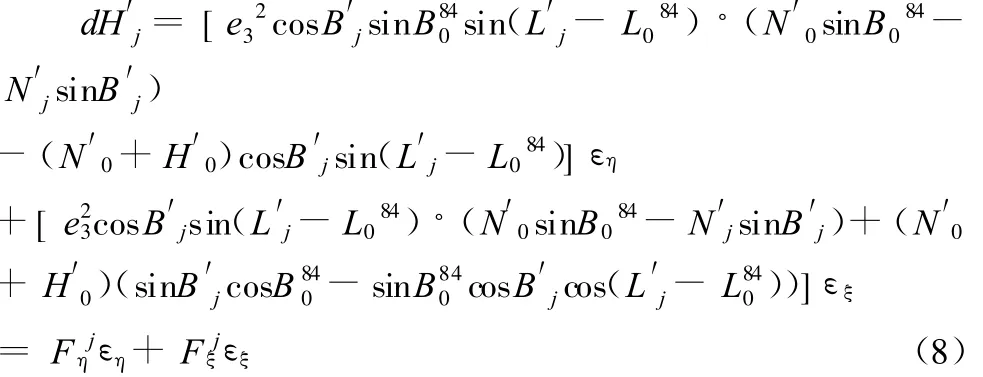
于是旋转后的椭球面与投影面之间的偏差则为:

以式(9)为函数模型,利用m个联测过水准的GPS点上求得的投影面与E3椭球面之间的垂向偏离 Δ H′j(j=1,2,…,m),可按最小二乘估计的方法来确定2个旋转角 εη,εξ。

式中,矩阵 A以(Fηj,Fξj) 为第 j个行向量,列向量L的第 j个分量为 Δ H′j。
4.4 调整E3椭球的定向和定位后任一点的空间直角坐标的求解
作为旋转中心,位置基准点P0的三维坐标仍保持不变,于是E3椭球的中心的平量为:
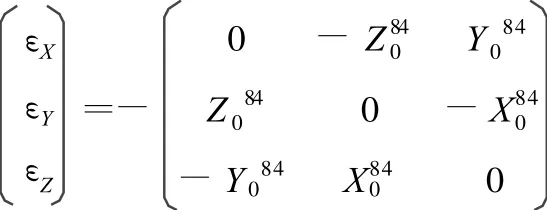
而平移、旋转变换后任一点Pi点的三维直角坐标为:

4.5 调整E3椭球的定向和定位后任一点大地坐标的求解
由上面求得的空间直角坐标(Xi,Yi,Zi)按 E3椭球的元素(a3,e32)即可求得新椭球面上的大地经纬度和大地高(Bi,Li,Hi)。由于改正了在点 P0处的倾斜角,就大大地减小了投影面与区域性椭球面之间的垂向偏离 Δ Hi=hi-Hi,且点P0处的大地经纬度(B084,L084)仍保持不变。由此利用多点定向定位确定了较优化区域性椭球面。
5 再变动E3椭球的元素
5.1 解算原理
为进一步减小投影面与区域性椭球面之间的垂向偏离Δ H″i=Hi-(hi-Δ h),还可在调整定向定位后再次利用多点法来改动E3椭球的元素。
仍然采用在调整E3椭球定向定位时用过的m个GPS水准联测点;文献[1]证得椭球元素变动量与大地高边动量的关系如下:

所以如果椭球元素变动后,在m个点上投影面与椭球面之间的垂向偏差vi为:

将式(13)代入即得:

对于在E3椭球定向定位后再次调整椭球元素的情况下,式中,其中Bi为调整E3椭球定向定位后的三维坐标所对应的大地纬度hi-Δ hi-,其中为把E3椭球定向定位后的三维坐标相应的大地高,在m个偏差vi平方和最小的条件下来求定da3,,即:

式中,矩阵 A以Ai为第i个行向量,列向量L的第i个元素为最后便可得出区域性椭球的新元素为:
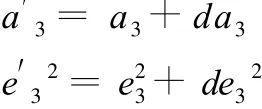
5.2 再次调整椭球元素后大地坐标的求解
由式(11)求得的空间直角坐标(Xi,Yi,Zi)按新椭球的元素(a′3,e′32)即可求得新椭球面上的大地经纬度和大地高(Bi,Li,Hi)。由于在定向定位后又对椭球元素进行了最小二乘调整,这就又一次减小了投影面与区域性椭球面之间的垂向偏离。由此而确定了最优化区域性椭球面。
6 结 语
通过单点确定E3椭球面和多点定向定位,得到了最优化的区域性椭球面,再通过坐标转换计算就能精确的将WGS-84参心坐标系中的三维坐标转换到地方独立坐标系。
[1]施一民,周拥军,张文卿.用定向定位调整法确定区域性椭球面 [J].测绘学报,2002(2):118-122.
[2]施一民.现代大地控制测量[M].北京:测绘出版社,2003.


