托柱转换结构的弹性抗震性能研究

吕剑勇

（广东科贸职业学院环境艺术系，广东广州 510430）

0 引 言

随着建筑功能的日趋复杂，高层建筑中设置转换层的情况已是非常普遍。现阶段转换构件的类型有梁、桁架、斜柱、拱、厚板等，其中，桁架又包括斜杆桁架和空腹桁架等形式。在上述几种转换构件当中，转换梁的截面往往很大，而桁架的上下弦杆可以分别设置在上下楼层，不占空间，便于转换层的使用，并且桁架的外形轻巧，能提高建筑的艺术性。此外，空腹桁架由于不设斜腹杆，有利于建筑门窗的布置，所以空腹桁架是一种非常理想的转换构件形式。

带转换层高层建筑是一类复杂高层建筑结构，由于抗侧力结构沿竖向不连续，不可避免地带来结构刚度和应力沿竖向的突变而形成结构薄弱层，导致其在地震作用下的传力机理十分复杂[1-8]。采用何种转换形式更有利于抗震，是科研技术人员必须面对和解决的问题。就转换构件本身而言，采用空腹桁架转换不但更能满足建筑功能要求，而且在静力性能上也具有一些优点，特别是对于托柱转换结构，空腹桁架转换比梁式转换具有更好的静力性能[9-10]。

为进一步研究空腹桁架转换结构在托柱时的抗震性能，文中以某托柱转换结构为计算模型，分析当采用空腹桁架转换时的基本动力特性和弹性动力时程响应，并与相同条件下的梁式转换结果相比较，以判别在托柱时采用空腹桁架转换的抗震可行性。

1 建立计算模型

采用结构分析程序SAP2000作为理论计算手段，建立三维空间有限元计算模型，如图1所示。

图1 某托柱转换结构计算模型

除转换构件分别采用转换梁和转换空腹桁架外，其余结构构件以及结构布置均相同。计算模型中的主要构件截面尺寸见表1。

表1 主要构件截面尺寸 mm

在SAP2000有限元模型中，梁、柱和空腹桁架杆件采用两节点空间框架单元，每节点有6个自由度;剪力墙和楼板采用空间4节点板壳单元，每节点有6个自由度，能够顺利地与空间框架单元协调[11]。

2 基本动力特性分析

文中计算了两种转换结构的前30个自振周期和振型，其中前三阶平动周期和前二阶扭转周期及相应的振型质量参与系数见表2。

表2 计算模型的自振周期 s

计算模型的一阶振型如图2和图3所示。

图2 梁式转换一阶振型图

图3 空腹桁架式转换一阶振型图

分析自振周期的计算结果，空腹桁架转换结构的前30个自振周期与梁式转换结构非常接近，仅低阶振型的自振周期略有差别，但相差仅为0.78%，而高阶振型的自振周期则完全相同。两种转换结构的振动形式和振型出现次序也非常一致，X方向前三阶平动振型分别出现在第1，4，19振型，Y方向前三阶平动振型分别出现在第2，5，25振型，前二阶扭转振型分别出现在第3，6振型。从振型质量参与系数来判别，两种转换结构均是以一阶振型为主。由此可见，在托柱时，空腹桁架转换结构与梁式转换结构的动力特性是非常相近的。

3 弹性动力时程分析

文中按照7度多遇地震来计算两种转换结构的动力时程响应，分别输入EL-Centro地震波-南北分量和唐山地震波-南北分量（北京饭店观测点），地震加速度时程曲线的最大值取35 gal，调整后的加速度时程曲线如图4所示。

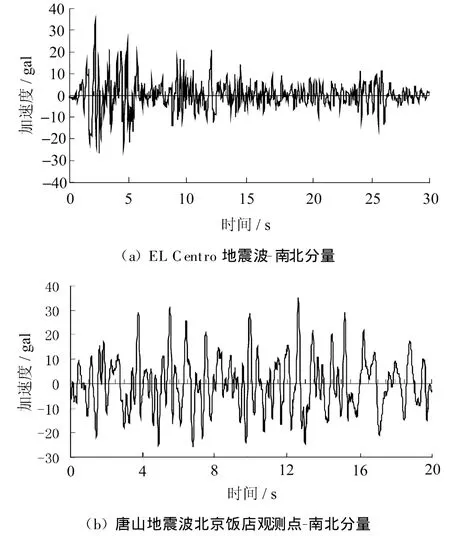
图4 调整后的加速度时程曲线

为简化工作，文中仅对两种转换结构的X方向作弹性时程分析。

计算模型在X方向的楼层剪力包络图如图5所示。

图5 计算模型在X方向的楼层剪力包络图

由图5可见，两种转换结构的剪力在底部几层略有不同，空腹桁架式转换结构在两条地震波作用下的剪力均略大于梁式转换结构，并且在转换层位置存在微小的剪力突变现象;在结构的中部和上部，两种转换结构的剪力分布基本相同。说明采用不同的转换构件对转换层附近的上下几层楼层剪力有所影响，但影响不大。此外，两种转换结构由唐山波引起的楼层剪力均大于EL-Centro波引起的楼层剪力。

计算模型在X方向的楼层侧移包络图如图6所示。

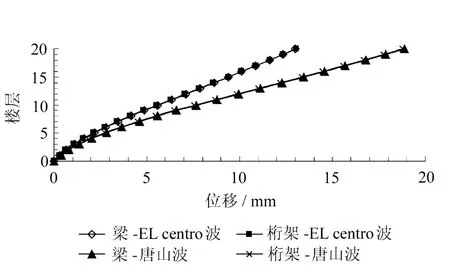
图6 计算模型在X方向的楼层侧移包络图

计算模型在X方向的层间位移角包络图如图7所示。

图7 计算模型在X方向的层间位移角包络图

由图6和图7可见，两种转换结构在两条地震波作用下的侧移包络曲线和层间位移角包络曲线均很接近，可以判别两种转换结构的整体抗侧刚度非常接近。在结构的下部几层，梁式转换结构的层间位移角略大于空腹桁架式转换结构，而在结构的上部几层，则情况相反。两种转换结构的最大层间位移角均出现在结构高度的3/4处。

4 结 语

1）从自振周期和振型的计算结果可知，空腹桁架转换结构与梁式转换结构的基本动力特性是非常相近的，两者的低阶振型自振周期存在微小差别，而高阶振型自振周期则完全相同，两者的振动形式和振型出现次序也完全一致。

2）从动力时程响应的计算结果可知，在转换层附近的几层，两种转换结构的楼层剪力略有差别，但差别不大。在地震波作用下，两者的楼层侧移和层间位移角基本相同，说明两者的整体抗侧刚度相当。

通过上述分析可以得出结论，在托柱情况下，采用空腹桁架转换与采用梁式转换在弹性阶段具有相近的抗震性能，采用空腹桁架作为转换构件在抗震上是完全可行的。

[1] 徐培福，王翠坤，郝锐坤，等.转换层设置高度对框支剪力墙结构抗震性能的影响[J].建筑结构，2000，30（1）:38-42，29.

[2] 王森，魏琏.不同高位转换层对高层建筑动力特性和地震作用影响的研究[J].建筑结构，2002，32（8）: 54-58.

[3] 赵西安.高层钢筋混凝土建筑结构抗震设计的一些建议[J].建筑结构，1994（4）:3-10.

[4] 姜华，魏群，焦涛，等.梁腹板开圆孔钢框架的抗震性能分析[J].河南理工大学学报，2008，27（3）:333-338.

[5] 刘伯栋，高大峰，张静娟.中承式钢筋混凝土拱桥结构动力特性研究[J].河南理工大学学报，2009，28（2）:175-179.

[6] 龚耀清，马伏龙.超高层建筑巨形框架与其基础地基共同工作的简化分析[J].河南理工大学学报，2006，25（2）:145-150，161.

[7] 龚耀清，杨博.超高层建筑空间巨形框架的半解析自由振动分析[J].河南理工大学学报，2005，24（1）: 65-68，73.

[8] 龚耀清，吴华芹，甄静水.超高层建筑空间巨形框架的地基、基础、上部结构共同工作的简化振动分析[J].河南理工大学学报，2007，26（3）:322-328.

[9] 吕剑勇.高层建筑梁式与空腹桁架式转换结构的比较研究[D]:[硕士学位论文].广州:华南理工大学，2007:7-25.

[10] 吕剑勇.空腹桁架转换结构的静力性能研究[J].建筑科学，2010，26（3）:62-65.

[11] 彭俊生，罗永坤.结构概念分析与SAP2000应用[M].成都:西南交通大学出版社，2005:1-67.