基于二次B样条的广义差分法

秦丹丹， 冯 雪， 左 平

（空军航空大学基础部，吉林长春 130022）

0 引 言

广义差分法从微分方程的积分守恒形式出发，通过选取试探函数空间为有限元子空间，检验函数空间为相应于对偶剖分的分段低次多项式函数空间来导出计算格式。文中介绍了基于二次B样条的广义差分法。B样条函数具有很多优良性质，如:有明确的表达式，具有有限支集、对称性和良好的光滑性等。因此，B样条函数作为试探函数空间的基函数可以保证系数矩阵的对称性、正定型和稀疏性。二次B样条广义差分法既保持了差分法的简单性，又兼具有限元的精确性。

1 B样条函数

m阶B样条函数Sm（x）[1]定义如下:

其中S1（x）为[0，1]上的特征函数。值得注意的是B样条函数的卷积定义式有下面的等价形式[2]:

由以上定义式可以得到三阶二次B样条函数的表达式:

显然，m阶B样条是分段m-1次多项式，且具有紧支集suppSm（x）=[0，m];此外，m阶B样条还具有如下性质:

1）Sm（x）是以 x=为对称轴的单峰值山丘状函数;

B样条性质的证明详见文献[2-3]。

2 基于B样条的广义差分法

考虑二阶常微分方程:

其中，p∈C（I），p≥0，f∈C（I），I=[a，b]。

对区间[a，b]进行均匀剖分，网格节点为a= x0＜x1＜…＜xn=b，且在区间[a，b]外分别扩充两点:x-2，x-1和 xn+1，xn+2，相邻节点间的距离记为h，记Ii=[xi-1，xi]。

构造基函数

则函数组{φi（x）}为区间[a，b]上以{xi}为节点的二次样条的一组基。

为方便处理边值条件，将前两个函数换成线性组合[4]:2φ-2（x），φ-1（x）-φ-2（x）。同时将最后两个基函数换成:φn-2（x）-φn-1（x），2φn-1（x）。变换前后基函数对应的函数空间是等价的。改换后的基函数称为变形的二次B样条基函数，仍记为{φi（x）}。在左端点处满足φ-2（x0）=1，φi（x0）=0（i≠-2），在右端点处满足φn-1（xn）=1，φi（xn）=0（i≠n-1）。

试探函数空间Uh取为满足边值条件的二次B样条有限元空间。由于文中考虑的是零边值问题，所以任一uh∈Uh可以表示成

式中:ci——待定系数;

uh——自由度为n，故试探函数空间的维数为n。

对偶剖分取为a=x0＜x1＜…＜xn=b，即对偶剖分与原剖分相同。检验函数空间Vh取为相应于对偶剖分的分段常数函数空间。检验函数为:

可见，检验函数空间与试探函数空间维数相同。

因此，基于二次B样条的广义差分格式[5]为:求uh∈Uh，使得

进一步应用分部积分公式，结合边值条件就得到微分方程的积分守恒形式如下[6]，求uh∈Uh，使得

在网格节点处取值非零的导数有:

通过研究学习，我们发现二次B样条广义差分法有以下误差估计[5，7-8]:

可以看出，二次B样条广义差分法不具有最佳L2收敛阶。

3 数值算例

在已知二阶常微分方程中，令a=0，b=1，p =0，f（x）=4π2sin（2πx）。此问题的精确解为u（x）=sin（2πx）。用uh（x）表示数值解，定义数值解在H1半模和L2模下的误差:

误差error1对应的收敛阶记为order1，误差error2对应的收敛阶记为order2。用n表示求解区间的剖分数。应用数学软件Matlab，得到误差与收敛阶数据见表1。

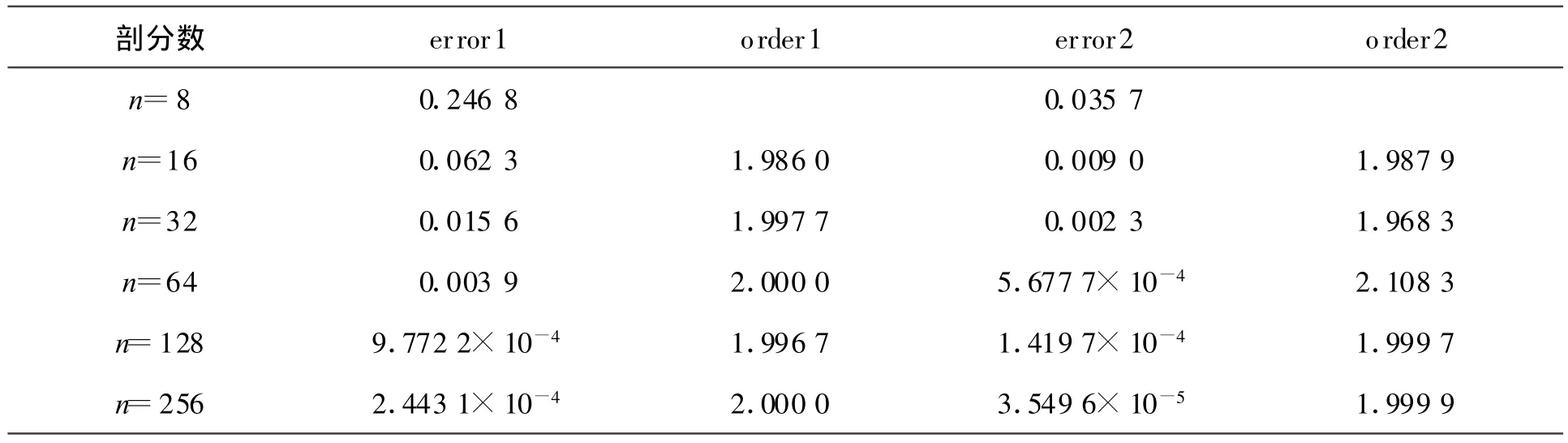
表1 误差与收敛阶

表中数据说明:随着网格剖分的加密，数值解与精确解越来越接近。在H1半模和L2模下，二次B样条广义差分法均具有二阶收敛精度。

4 结 语

当试探函数空间为Lagrange型二次元时，相应于节点和半整节点存在两组不同的基函数，而二次B样条有限元空间只有相应于节点的一组基函数，因此，两种方法的系数矩阵阶数之比约为2∶1。此外，B样条有限元可以保证位函数的光滑性。但是，二次B样条广义差分法不具有最佳L2收敛阶，这个缺点在一次和三次B样条广义差分法中可以得到避免。因此，在广义差分法中，关于试探函数空间的选取仍然是至关重要的。

[1] 陈广生.B样条函数的一个性质[J].广西科学，2008，15（4）:381-382.

[2] 梁学章，李强.多元逼近[M].北京:国防工业出版社，2005.

[3] 孙家昶.样条函数与计算几何[M].北京:科学出版社，1982.

[4] 梁旭彪，简柏敦，倪正光.B样条有限元法[J].中国电机工程学报，1987，7（6）:9-20.

[5] LI Rong-hua，CHEN Zhong-ying，WU Wei.Generalized difference methods for differential equations [M].New York:Marcel Dekker Inc.，2000.

[6] 高广花，王同科.两点边值问题基于三次样条插值的高精度有限体积元方法[J].山东大学学报，2009，44（2）:45-51.

[7] CHEN Zhong-ying.Error estimates for generalized difference method[J].Acta Sci Natur Univ Sunyatseni，1994，33（4）:22-28.

[8] CHEN Zhong-ying，LI Rong-hua，ZHOU Ai-hui. A note on the optimal-estimate of the finite volume element method[J].Advances in Computational M athematics，2002，16（4）:291-303.