改进的Hough变换圆检测算法
尚璐,李锐,宋信玉
(重庆大学光电技术及系统教育部重点实验室,重庆400030)
快速而准确地检测出圆及其参数是计算机视觉和模式识别中的一项重要研究内容,在机器视觉自动测量系统、智能检测等领域有着广泛的应用前景。标准Hough变换[1](Standard Hough Transform,SHT)检测圆是一种最传统的检测算法。它的最大优点是:对噪声不敏感,检测后可有效去噪;而且在圆变形,甚至部分区域丢失的情况下仍然可以得到比较理想的结果。
Hough变换的基本思想是将图像空间中具有一定关系的像元进行聚类,寻找能把这些像元用某一解析形式联系起来的参数空间累积对应点。但由于圆有3个自由参数,需在三维参数空间中进行累积,使得这种做法因计算量和内存需求量过大而不合实际。为了克服这些缺点,XU[2-3]等提出了随机Hough变换(Randomized Hough Transform,RHT),在图像空间随机地选取非共线的三个点映射成参数空间的一个点,是“多对一”的映射。当用RHT处理简单图像时,它表现出相当优异的性能,但在处理复杂图像时,由于随机采样引入大量的无效采样和累积,使算法的性能下降。为此,很多学者提出了改进的RHT算法。如:利用圆内接直角三角形长边过圆心的性质[4],对圆参数进行求解;以随机采样到的2个图像点及在此两点的中垂线上搜索第3个图像点来确定候选圆[5];利用圆边缘上各点梯度所在的直线过圆心的特点,对选取的任意三点进行约束[6]。它们都有效的减少了“多对一”映射的计算量,同时使用动态链表结构降低了参量分配空间,但随着圆和噪声的增多,随机采样的无效累积增多,性能将大大降低。此外,林金龙等提出的一种用点Hough变换实现圆检测方法[7],极大地降低了计算复杂性和对资源的需求;Chen等提出了一种非RHT的随机圆检测算法(Randomized Circle Detection,RCD)[8],它在中等以下的噪声比情况下检测速度较RHT快。本文提出一种改进的Hough变换圆检测算法。利用圆为中心对称图形的几何特征,通过Hough变换计算出圆心,然后再进行一次Hough变换计算出圆半径。该算法不仅有效提高了圆检测效率,而且在圆和噪声增多时,性能不会降低。
1 原理
圆的标准方程为:

式中含有3个参数。在本文算法中,3个参数并不是一次性求出,而是分两步求出:第一步求出圆心,这是该算法的核心;第二步求出圆半径。
1.1 圆心的检测
假定数字图像大小为M×N,经过边缘检测得:

式(2)中Pij表示第i行第j列像素点灰度值(0≤i<M,0≤j<N)。
假设圆心坐标为(a,b),图1(a)中hi为数字图像中第i行的水平扫描线。li,mi为hi与圆的两个交点,ni为li和mi的中点。它们满足:

由于圆是中心对称图形,故圆心的横坐标必定在直线x=a上。

所以可以通过对每一行进行扫描,找出这样的对称点,并在一维空间中采用Hough变换对它们的中点进行累加计数,计数最大值对应的参数坐标即为a的值。
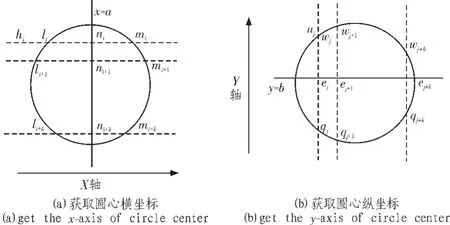
图1 圆心的获取Fig.1 Detect circle center
同理,图1(b)中uj为数字图像中第j列的垂直扫描线,wj,qj为uj与圆的两个交点,ej为wj和qj的中点。它们满足:

由于圆是中心对称图形,故圆心的纵坐标必定在直线y=b上。
所以可以通过对每一列进行扫描,找出这样的对称点,并在一维空间中采用Hough变换对它们的中点进行累加计数,计数最大值对应的参数坐标即为b的值。
这样通过对称点的Hough变换就可以计算出圆心(a,b)。
1.1.1 单 圆圆心检测
计算单圆圆心横坐标a的算法步骤:
1)遍历整幅图像,找出满足以下条件的像素点pxj。
①像素点为非边缘点pxj(与行数x无关)。
②对pxj的左右相邻像素点进行搜索,找到左右相邻的第一个边缘像素点,记为mxp(向左搜索),lxq(向右搜索)。

(pxj,mxp,lxq取横坐标值)
2)在一维空间中采用Hough变换对满足条件的pxj进行A(Pxj)累加计数。
3)参数空间中A(Pxj)最大值对应的pxj即为圆心横坐标,a=pxj(pxj取横坐标值)。
同理可以计算出单圆圆心纵坐标,b=pix(pix取纵坐标值)。
这样就求得了圆心坐标(a,b)。
1.1.2 多 圆圆心检测
多个圆的圆心检测与单个圆的圆心检测类似。在数字图像中,圆周包含的像素点越多,圆的半径就越大。根据这一性质,可知半径越大的圆,圆周中包含的对称点就越多。故在检测N个圆的圆心时,参数空间中A(Pij)最大的N个值所对应的Pij即为它们的圆心坐标。
1.2 半径累积
利用圆心坐标(a,b),将边缘像素点pij代入圆方程(x-a)2+(y-b)2=r2,计算出一个候选半径r,在一维空间中采用Hough变换对候选半径r进行累加计数。看r的计数值A(r)是否大于构成圆允许的最小点数Tm=λ×2πr(λ为比例系数,本文中λ=0.8)来确定真圆,r即为该圆的半径。
2 复杂度分析
在标准Hough变换检测圆算法中,由于圆有3个自由参数,需要在三维参数空间中进行累积,共进行N3次计算(假设图中有N个像素点),复杂度函数为:

按照本文的方法,对复杂度进行分析。计算圆心时,在一维空间中进行累加计数求出圆心坐标,共进行了2×N次计算,复杂度函数为:

同理,计算半径时,共进行了N次计算,复杂度函数为:

故本文算法在执行时共进行了3×N次计算,复杂度函数为:

O(N3)远大于O(3N),由此可见,检测效率大大提高。
3 实验结果
本文的所有实验都是在248 MB内存的Celeron1700 MHz计算机上用VC++6.0编程实现的。
3.1 实验1
实验1采用的图像如图2(a)所示,其大小为280×220,图中含有3个已知圆,图2(b)为用Kirsch算子提取的边缘图像,图2(c)为半径累积的描述图,表1为用SHT,RHT和本文算法对图2(b)分别进行检测的平均执行时间的比较结果(执行50次)。表2为用本文算法对图2(b)进行检测的检测值与真实值的比较。

图2 实验图像的检测结果Fig.2 Result of detected value

表1 检测平均执行时间比较结果Tab.1 Comparison of runtime
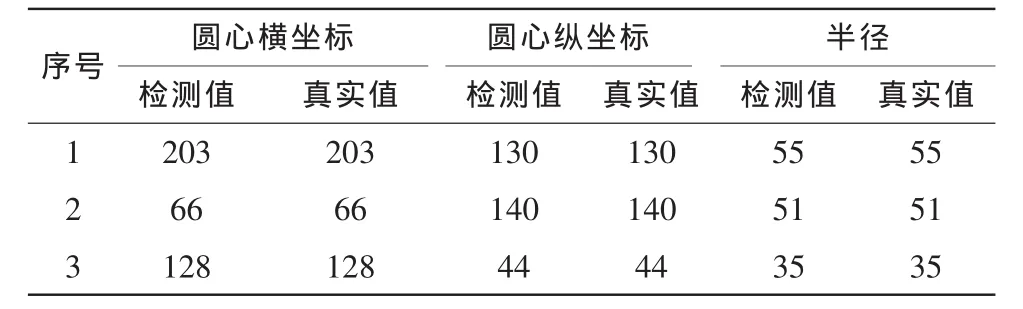
表2 本文算法对图2(b)的检测结果Tab.2 Result of detected value of image2(b)
由表1可知,对于图2(a)所示的合成图像,用本文算法检测圆的速度明显快于SHT算法和RHT算法,执行时间大大缩短。
3.2 实验2
在实验2中,对图像中含有1~5个圆(图3(a)含有2个圆,图3(c)含有5个圆)的情况,用RHT,RCD和本文算法(单幅图像大小为280220)分别进行检测。图4为3种算法平均执行时间的比较(执行50次)。表3为图3(c)中5个圆的检测值与真实值的比较。

图3 实验图像Fig.3 Imgae of experiment

图4 实验2中3种算法平均执行时间比较Fig.4 Comparison of runtime of experiment 2
为了检测本文算法的抗噪性能,在图3(a)中任意加入了不同程度的噪声,噪声比大约为25%~150%。图3(b)所示为在图3(a)中增加了759个噪声点的图像。图5为图3(a)和它增加不同比例的噪声后分别用RHT,RCD和本文算法检测平均执行时间的比较(执行50次)。

图5 实验2中3种算法平均执行时间比较Fig.5 Comparison of runtime of experiment 2
由实验2可以看出,检测单个圆时,本文算法与RCD检测算法的执行时间都非常短,比RHT检测算法快了一个数量级。当圆的个数和噪声增加时,RHT检测算法和RCD检测算法的执行时间呈线性增加,而本文算法的执行时间几乎没有变化。
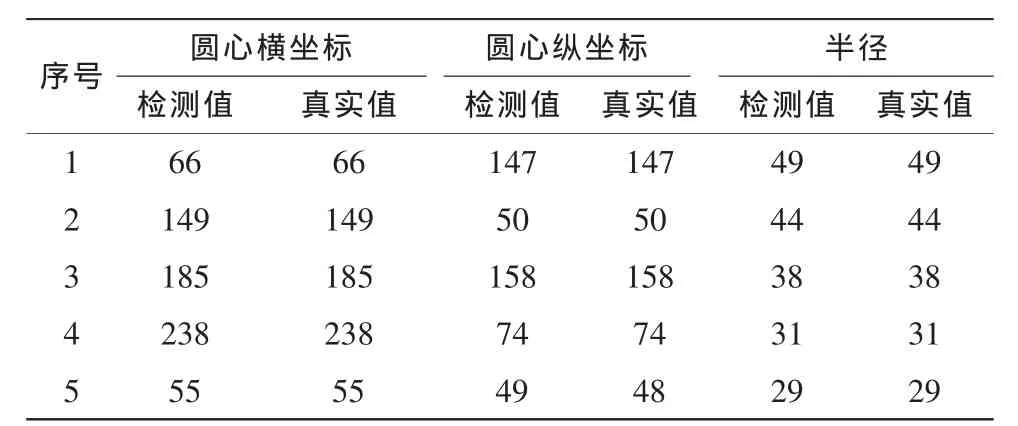
表3 本文算法对图3(c)的检测结果Tab.3 Result of detected value of image3(c)
4 结论
提出一种改进的Hough变换圆检测算法。该算法不仅保留了标准Hough变换的优点,对噪声不敏感,而且由于利用圆对称点的几何特征进行Hough变换来检测圆心,使执行时间明显少于标准Hough变换,计算量也低于其他采用几何性质来减少Hough变换维数的算法,对单个圆和多个圆同样有效,具有较高的实用价值。
[1]Hough P V C.Method and means for recognizing complex patterns[P].US:Patent 3069654,1962.
[2]XU L,OJA E.A new curve detection method:Randomized Hough Transform(RHT)[J].Pattern Recognition Letters,1990,11(5):331-338.
[3]XUL,OJAE.Randomized hough transform:basic mechanisms,algorithms and computational comp lexities[J].Image Understanding,1993,57(2):131-154.
[4]商飞,王丰贵,田地,等.一种基于圆内接直角三角形的圆检测方法[J].光学学报,2008,28(4):739-743.
SHANG Fei,WANG Feng-gui,TIAN Di,et al.A method for circle detection based on right triangles inscribed in a circle[J].Acta Optica Sinica,2008,28(4):739-743.
[5]黎自强,滕弘飞.广义Hough变换:多个圆的快速随机检测[J].计算机辅助设计与图形学学报,2006,18(1):27-33.
LI Zi-qiang,TENG Hong-fei.Generalized Hough transform:fast randomized multi-circle detection[J].Journal of Computer-Aided Design&Computer Graphics,2006,18(1):27-33.
[6]陈燕新,戚飞虎.基于随机Hough变换的快速圆检测方法[J].上海交通大学学报,1998,32(10):17-20.
CHEN Yan-xin,QI Fei-hu.Fast circle detection using randomized Hough transform[J].Journal of Shanghai Jiaotong University,1998,32(10):17-20.
[7]林金龙,石青云.用点Hough变换实现圆检测的方法[J].计算机工程,2003,29(11):17-18.
LIN Jin-long,SHI Qing-yun.Circle recognition through a point Hough transformation[J].Computer Engineering,2003,29(11):17-18.
[8]CHEN Teh - chuan , CHUNG Kuo - liang . An efficient randomized algorithm for detecting circles[J]. Computer Vision and Image Understanding,2001,83(2):172-191.

