基于距离—矩法判据的多源寿命信息融合

王春晖，李忠东

（1.海军装备部飞机办，北京 100841；2.海军驻沈阳地区航空军事代表室，沈阳 110034）

在可靠性分析和参数估计中，Bayes方法已广泛应用，多种验前信息的运用使武器装备的试验分析可以在小子样的场合下进行。Bayes 分析要解决的关键问题是验前分布的确定问题，其中的难点就是多源验前信息的融合，即要在综合利用各种验前信息的前提下，得到合理的融合验前分布。本文所说的多源验前信息是指来自历史上多台类似型号产品的试验和运行数据、仿真数据、专家意见等。[1]

现有的融合方法主要有以下几种：基于可信度的多源验前信息融合方法[2]；采用Bayes相继律[3]融合多组寿命数据或多个专家的信息，最大熵准则融合方法[4]；专家设定融合权重[5]。这些方法各具优缺点和适用范围。可信度融合方法比较合理，但可信度的计算较为困难。最大熵方法随着验前信息的增多，推导出的验前分布的形式愈加复杂，给验后分布的求取及Bayes 推断带来了一定的计算困难。而专家设定权重的方法简便易操作，但具有难以克服的主观随意性。

本文以矩法理论为前提，采用欧氏距离作为融合判据，提供一种信息融合的新方法，既考虑了各源验前信息的可信度又简化了算法的复杂性。

1 理论基础

矩法估计是用样本矩(已知量)去估计总体矩(含有未知参数)，即用样本矩度量总体矩，由此而得参数的估计，即矩法估计量。

聚类分析与判别分析中常用各种距离作为度量[6]，以描述样本之间的关联程度[7]。信息融合理论中也经常采取利用欧氏距离作为判别两证据之间的关联程度[8-9]，为简化运算，本文以欧氏距离为融合度量对多源信息进行距离融合。

对不同来源的数据，特别是类似产品的可靠性数据不能直接用在新产品的可靠性评估中。为了在新产品可靠性评估中利用类似产品可靠性信息，首先应确定类似产品的可信度。通常，可信度由可靠性专家根据自己对两个类似产品的了解来确定。[10]下面即以距离判据计算各先验信息的可信度。

以各来源数据与现场试验数据做距离判别，距离越接近则越可信，距离越远则可信度越低。因此定义可信度为：

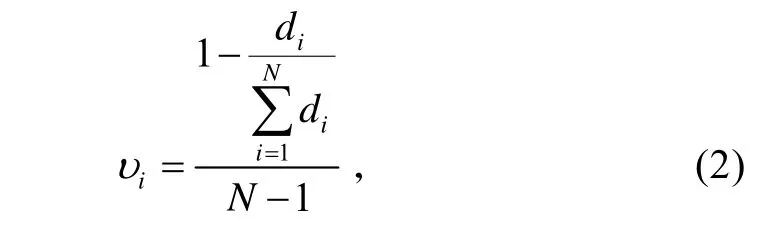
即归一化权重之和应对每一项除以N−1。

2 融合算法

2.1 基本假设

不妨设多源信息(历史信息、仿真数据等)为

式中：N为信息来源数量；(Ki,Ti)表示在时间 Ti内发生Ki次故障。现场试验数据为E0=(K0,T0)。

假设E 中的每一个样本组都可用一个poisson过程来描述，即：

其中，λi为瞬时失效率。

由Poisson过程的特性可知，此假设在工程实践中具有普遍适用性。λi可通过E的第i个样本组信息(Ki,Ti)估计得到，λi的极大似然估计为：

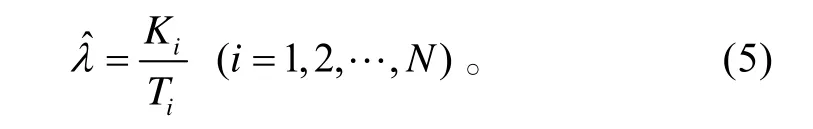
同时可以得到，λi的均值和方差分别为E [λi]和D [λi]。这里我们考虑多源信息的可信程度，引入加权均值m和加权方差 s2。其中：

2.2 算法步骤

1)计算可信度。根据上述方法求解各源先验信息的可信度，为先验信息融合提供依据。此时多源验前信息已经转化为瞬时失效率 λi(i=1,2,… N)，与其相应的可信度 vi(i=1,2,…,N)。

2)计算加权期望和加权方差。根据式(5)、(6)计算 λi(i=1,2,…,N)的加权均值和加权标准差。

3)验前分布的参数求解。由矩法估计原理，不同的随机变量可能拥有相同的期望和方差。对于未知总体的先验分布，可以求解各种可能分布函数在期望和方差分别为m和s2时的参数值。

下面以几种常见的分布函数为例：

① 正态分布。

② 对数正态分布。

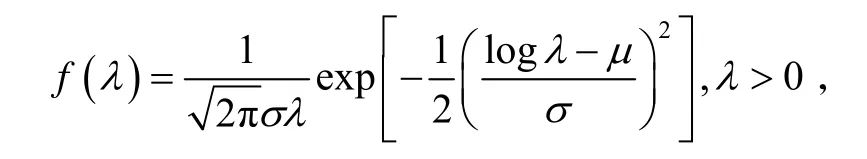
③ Gamma分布。

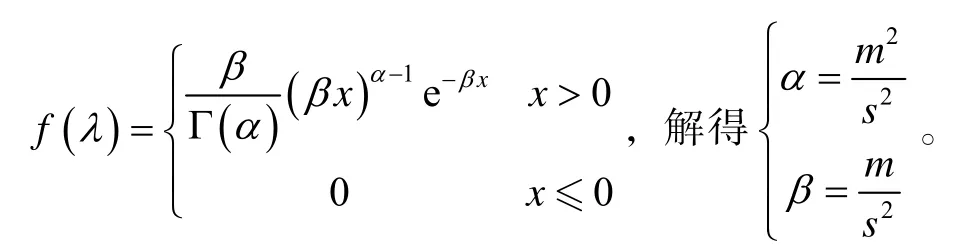
④ 威布尔分布。

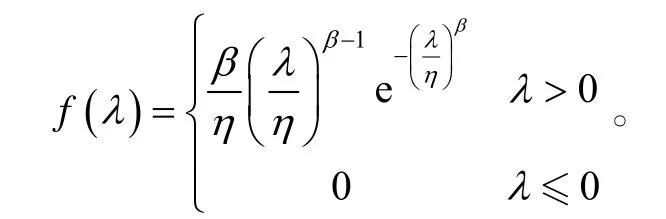
4)确定验前分布。计算各先验信息与各可能验前分布的距离，距离越小则说明先验多源信息与该种分布的相容程度越高。由于此时的先验分布是λ的函数，因此先验信息点集为(λi,vi)，(i=1,2,…,30)。

5)计算融合后的具有贴近度权重的验前分布函数。

3 仿真算例

某新型发动机的现场资料为E0=(K0,T0)=(1 0,4)。该型发动机继承了前一型号产品的大部分技术特性，积累了大量历史数据：[1]E={(Ki,Ti)}={(4,15),(40,12),(0,8),(10,8),(14,6),(31,5),(2,5),(4,4),(13,4),(4,3),(27,4),(14,4),(10,4),(7,2),(4,3),(3,3),(11,2),(l,2),(0,2),(3,1),(5,1),(6,1),(35,5),(12,3),(1,1),(10,3),(5,2),(16,4),(14,3),(58,11)},(i=1,2,…,30)。

将原始多源先验信息分别带入式(2)、(5)得到各源信息的可信度 vi(i=1,2,…,30)，和瞬时失效率λi(i=1,2,…,30)。

将(λi,vi)，(i=1,2,…,30)的代入式(6)、(7)得到加权均值m=2.968，加权方差s2=4.293。

由加权均值和加权方差解得各可能分布参数如表1所示，计算各验前信息到各个可能验前分布的距离，结果如表2所示。

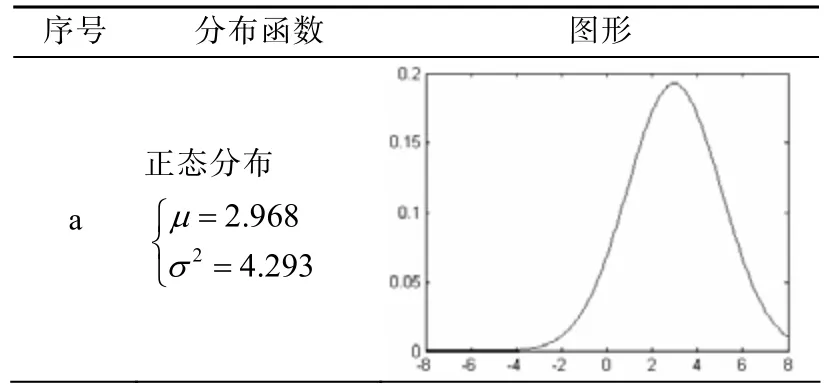
表1 加权均值和加权方差可能分布参数表

由此可见选取Gammar分布作为融合先验分布可以使得其与各先验信息的相容性最强。

4 结论

本融合算法完全从数据本身出发，在考虑了各信息源可信度的情况下，简化了算法易于计算。

进一步工作展望：进一步研究应扩展所讨论的分布函数的种类，使算法的应用范围得以扩大。

[1]冯静.小子样复杂系统可靠性信息融合方法与应用研究[D].长沙∶国防科学技术大学,2004.

[2]黄寒砚,段晓君,王正明.考虑先验信息可信度的后验加权Bayes 估计[J].航空学报,2008,29(5)∶1245-1251.

[3]柴建.系统可靠性评估中的信息融合方法及应用[D].西安∶西北工业大学,2006.

[4]XIE M,HONG G Y,WBHIIN C.Software reliability Prediction incorporating information from a similar Project[J].The Journal of System and Software,1999,49∶43-48.

[5]LESLEY W,JOHN Q.Building Prior distributions to support Bayesian reliability growth modeling using expert judgment[J].Reliability Engineering and System Safety,2001,74∶117-128.

[6]唐旭清,朱平,程家兴.基于归一化距离的结构聚类分析[J].模式识别与人工智能,2009,22(5)∶678-688.

[7]李玉榕,项国波.一种基于马氏距离的线性判别分析分类算法[J].计算机仿真,2006,23(8)∶86-88.

[8]杨威.基于信任函数理论的不确定性信息融合技术研究[D].长沙∶国防科学技术大学,2008.

[9]尹学忠,王杰贵.一种异类源信息融合中证据冲突问题的解决方法[J].宇航学报,2009,30(4)∶1663-1685.

[10]方良海.产品可靠性评估中的多源信息融合技术研究[D].合肥∶合肥工业大学,2006.