我国保险资金投资资本市场的实证研究

张 帅，朱浩然

〔中央财经大学保险学院，北京100081〕

一、研究的背景

从当代国际保险市场发展看，保险资金运用和保险业的发展已经融为一体，保险承保业务和保险资金运用业务并重也已成为现代保险业的共识。2011年是我国加入WTO的第10个年头，也是“十二五”的开局之年，随着我国不断对外开放，我国保险业面临着结构的调整和升级。目前，我国保险市场份额竞争日趋激烈，相关保险费率有进一步降低的趋势，保险公司的承保压力日益增大。因而，今后保险业的发展必将更加依赖于资金运用业务，可以说，资金运用业务能否正常稳定发展，是事关保险公司长远发展的根本。我国自1980年恢复保险业务以来，保险资金运用经历了无序阶段、规范阶段和快速发展阶段。截至2010年12月底，我国保险业总资产突破5万亿元，保险资金运用余额达到4.6万亿元。但是，我国保险资金投资收益率一直都处于较低水平，从2000年到2010年，我国保险资金投资的平均收益率仅为4.6%，而相同的时期内，主要发达国家的保险资金投资平均收益率普遍维持在10%左右。我国保险资金很大一部分投资于银行存款是造成投资收益率过低的主要原因，所以，我们要进一步拓宽保险资金的投资渠道，加大我国保险资金投资资本市场的力度，但如何优化资本市场投资组合，以使保险公司获得最大单位风险收益是保险业界和学术界正在面临的问题。

David Cummins从理论上构建了保险公司投资组合的优化模型，并结合美国保险市场数据对其进行实证研究，但是其模型假设收到的所有保费都可以作为投资资金来源，没有考虑税收和经营费用对保险资金的影响。陈辉主要从我国保险资金投资组合的风险度量角度对我国保险资金的投资进行研究，文章并没有对投资组合的最优构成进行实证分析。郝佳运用Markowitz的投资组合理论对我国保险投资组合的选择进行了实证研究，但仅以平安保险为例，没有站在整个行业的高度，且缺乏理论的探讨。本文的研究建立在前人研究的基础上，通过对David Cummins保险资金运用模型的简化和改进，结合我国保监会最新实施的《保险资金运用管理暂行办法》，对我国保险市场数据进行实证研究，并根据实证研究的结论为我国整个保险行业投资资本市场提出相关的建议和对策。

二、保险资金投资资本市场的必要性

保险资金是保险公司通过各种渠道聚集的各种资金的总和，一般意义上的保险资金包括公司股东投入的资本金、保证金、营运资金、公积金、公益金、未分配盈余、保险保证基金、各种保险准备金和其他资金。保险资金是保险企业偿付能力的保证，从一定意义上讲，保险资金只能运用于补偿被保险人的经济损失，不能用于其他方面的投资。但是，由于保险合同的射悻性，保险公司聚集的保险资金和保险给付往往存在一定的时间差，尤其是寿险公司，保险资金具有长期的稳定性，这赋予了保险公司极其有利的投资条件。保险资金运用同一般的资金运用一样，需要遵循“安全性”、“收益性”和“流动性”等原则。

资本市场是期限在一年以上的中长期金融市场，按市场工具来划分，资本市场通常由股票市场、债券市场和投资基金市场构成。资本市场能够为保险资金提供与之匹配的、同时满足“三性”要求的投资工具，也就是说，保险资金与资本市场的投资工具之间存在着天然的匹配关系。目前，保险资金进入资本市场，与资本市场联动发展，已成为世界各国和地区的普遍做法。随着我国保险业和资本市场的快速发展，保险资金投资资本市场具有了更加重要的意义:

1.有利于增强保险公司的偿付能力

偿付能力充足是对保险公司的最基本要求。目前，我国保险公司的偿付能力与国际保险业相比还有很大的差距。保险资金运用于资本市场，有利于保险公司拓展新业务，提高投资收益，增强保险公司的偿付能力。

2.有利于完善保险公司的资产负债匹配

由于保险业承担着风险分摊和损失补偿等职能，保险资金有着强烈的投资冲动。资本市场上多种多样的投资工具和丰富的投资组合，为保险公司提供了不同性质、不同期限、不同利率的投资品种，扩大了保险公司资产和负债匹配的空间，满足了不同情况下的负债对资产的匹配性要求和保险资金对流动性的要求。

3.有利于缓解保险公司的承保压力

随着我国保险市场份额竞争日趋激烈，相关保险费率有进一步降低的趋势，保险公司的承保压力日益增大。而保险公司把资金投向具有较高收益的股票、基金等资本市场投资工具，将会显著提高保险公司的投资收益率，从而有效地缓解保险公司承保环节的压力。

三、保险资金投资资本市场的Granger因果关系检验

1.理论基础

格兰杰(Granger)1969年提出格兰杰因果关系检验(Granger test of causality)，对于两变量X与Y，格兰杰因果关系检验要求估计一下回归:

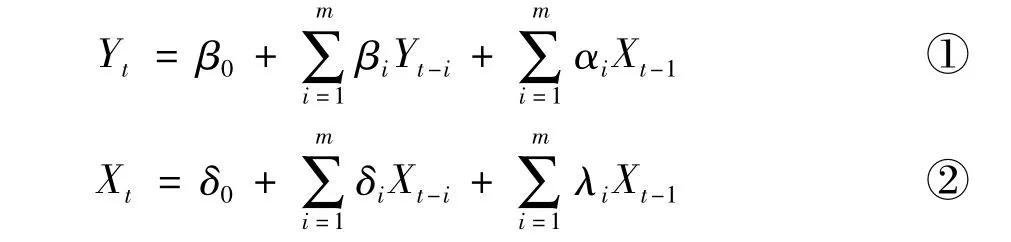
可能存在四种检验结果:

(1)X对Y有单向影响，表现为①式中X的各滞后项前的参数整体不为零，而②式中Y的各滞后项前的参数整体为零;

(2)Y对X有单向影响，表现为②式中Y的各滞后项前的参数整体不为零，而①式中X的各滞后项前的参数整体为零;

(3)Y与X之间存在双向影响，表现为Y与X的各滞后项前的参数整体不为零;

(4)Y与X之间不存在影响，表现为Y与X的各滞后项前的参数整体为零。

格兰杰检验是通过受约束的F检验完成的。如针对X不是Y的格兰杰原因这一假设，可以构造F统计量:

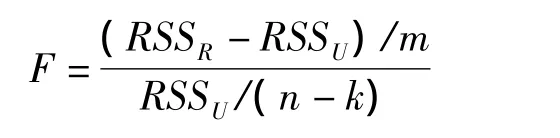
其中，RSS为残差，m为X的滞后项的个数，n为样本容量，k为包含可能存在的常数项及其他变量在内的无约束回归模型待估参数的个数。

需要指出的是，格兰杰因果关系检验对于滞后期长度的选择有时很敏感。不同的滞后期可能会得到完全不同的检验结果。因此，一般而言，常进行不同滞后期长度的检验，以模型中随机干扰项不存在序列相关的滞后期长度来选取滞后期。

2.Granger因果检验

设定两个基本变量Y和X，分别表示资本市场流通市值增长率和保险资金投资收益率。选择变量的样本区间为2000年至2010年，数据为年度数据，如表1所示:

表1 资本市场流通市值增长率与保险资金投资收益率 单位:%

使用Eviews5.0对资本市场流通市值增长率序列与保险资金投资收益率序列作 Granger因果检验，结果如表2所示:

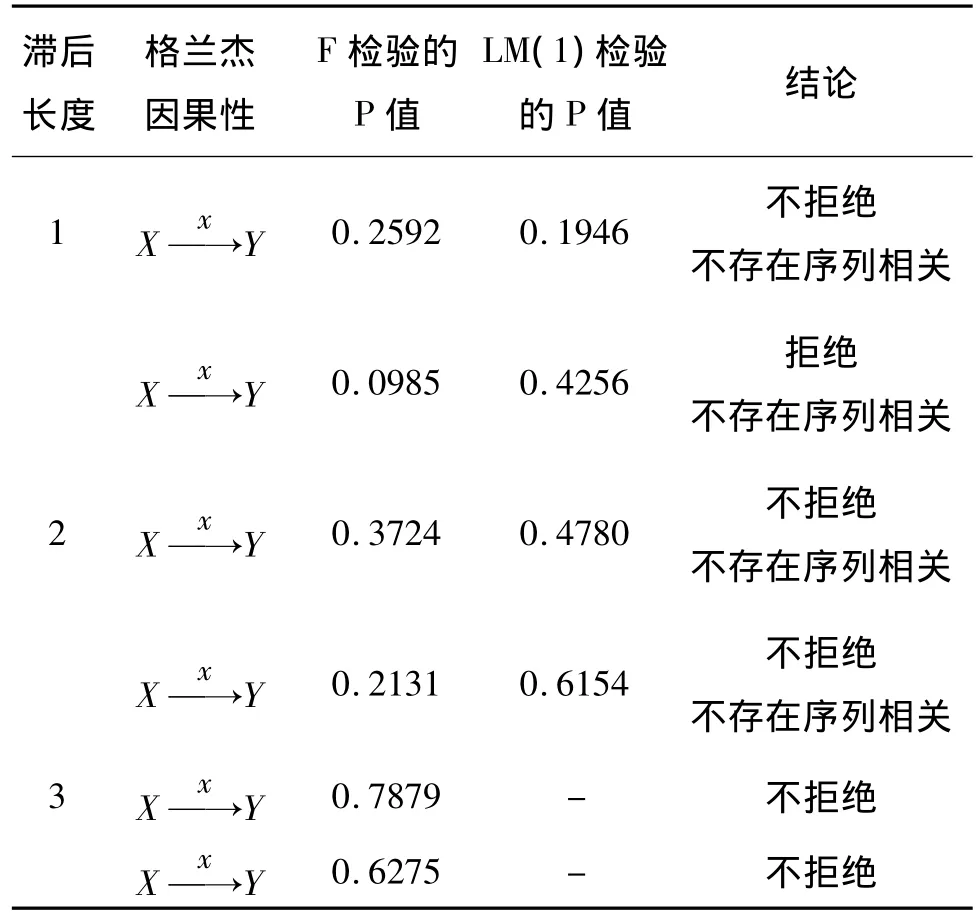
表2 Granger因果关系检验结果

分析以上Granger因果检验结果可知，我国保险资金投资收益率不是我国资本市场流通市值增长率的格兰杰原因，而我国资本市场流通市值的增长率是我国保险资金投资收益率的格兰杰原因。这充分表明，大力发展我国资本市场，推进保险资金在资本市场的运用对于提高我国保险资金收益率具有重要的意义。接下来笔者将利用Markowitz理论研究保险资金投资组合优化问题，为我国保险资金运用提供参考。

四、保险资金投资资本市场整体投资组合的优化

1.投资组合模型的建立

保险公司的投资组合问题涉及多种保险产品和投资对象以及长期匹配和风险收益权衡的问题。本文模型主要以Markowitz的投资组合理论为基础，用期望代表投资组合的收益率，方差代表投资组合的风险，研究单位风险收益最大化的决策。此外，对David Cummins的保险公司投资收益模型进行简化，将新参数——保险杠杆引入模型，从而使模型更适合实证分析。

假设保险公司的利润来源为承保收益和投资收益，投资收益包括无风险资产投资收益和风险资产投资收益，不考虑投资手续费等费用。

则保险公司的收益可表示为:

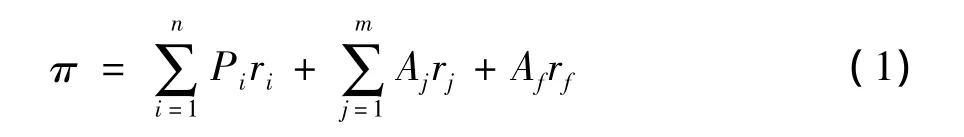
其中:π表示在某个特定期间保险公司的净利润;

Pi表示保险公司提供的第i种产品所收取的保费总额;

ri表示第i种产品的保费利润率，即该种产品带来的利润与该种产品保费收入的比例;

Aj表示保险公司对投资对象j投资的金额，rj表示投资对象j带来的投资收益率;

Af表示在无风险资产(本文中指银行存款)投资的金额，rf表示大额存款协议利率或同期一年期银行存款利率。

总资产收益率可表示为rp=，T表示总资产。

总资产收益率可以进一步表示为:

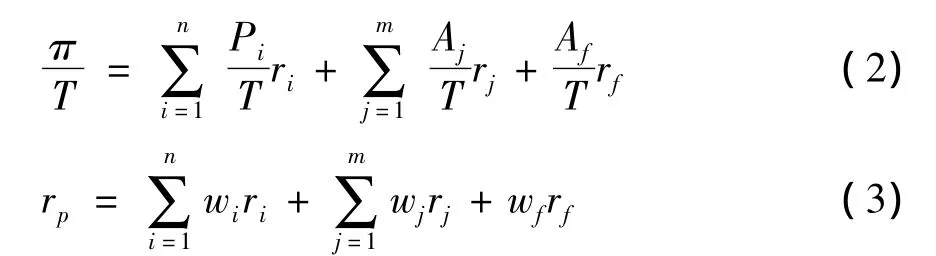
wi表示第i种保险产品的保费收入与其总资产的比率，在一定程度上反映了保险杠杆(insurance leverage，保费收入与净资产的比率)，wj及wf是指投资杠杆(investment leverage)。再假设，保险资金的来源为当年保费收入与自有资金之和减去赔款支出、经营费用等(在接下来的数据计算中需要转化为可运用资金)。若设保险公司可运用资金的比例占总资产的比例为g，则:

两边同时除以T可以得到:

对于方程(3)，两边取期望及方差可以得到:

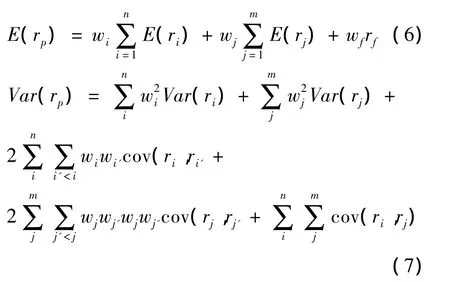
因此保险公司的最优投资组合优化问题可表示如下:

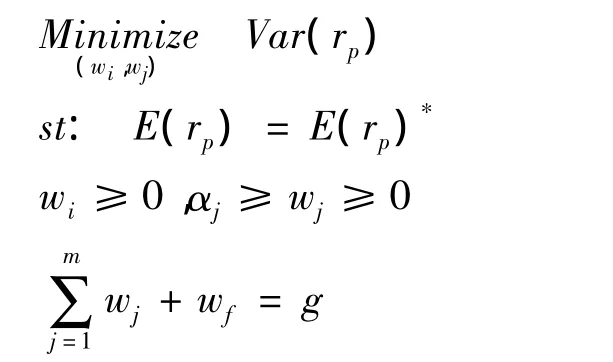
其中E(rp)*为常数，为了讨论在特定收益率下风险最小时的投资组合设置，αi表示投资比例上限。

2.我国保险行业最优投资组合构建

(1)数据获取

无风险投资收益率。根据《保险资金运用管理暂行办法》，保险公司投资于银行存款和国债的比例不得低于5%，因此可以将国债和银行存款作为无风险资产。保险公司银行存款主要分为定期存款和大额协议存款两种，大额协议存款利率往往是保险公司的商业秘密，基于数据的可获得性(并不影响模型的理论意义)，取以往年度一年期及五年期定期存款利率和国库券利率的平均值作为无风险资产收益率。

股票投资(资产1)收益率。由于保险资金在多种股票上进行资产配置，笔者采用上证综指收益率代替股票投资收益率。

企业债券投资(资产2)收益率。选取上海证券交易所公布的五年期企业债券的收益率平均值作为企业债券投资收益率。

基金投资(资产3)收益率。选取新浪财经的基金指数增长率作为收益率。

保险产品保费收入和承保收益率。本文对我国寿险和财险进行综合考虑，以保险行业的利润总额减去投资收益作为承保利润的近似，除以保险原保费收入即得承保收益率。

比例限制。由于国家保险监督管理机构规定的投资比例限制为投资额与总资产的比例，经过笔者的计算，近三年保险公司可运用资金与总资产的比例平均约为92%，因此，可以将投资额对总资产的比例限制转化为对可运用资金的比例限制:wf≥5.433%。

根据保监发(2010)66号文件，股票和证券投资基金的投资额不得超过上季末总资产的25%，可表示为w1+w3≤0.2717;

投资于无担保企业(公司)债券和非金融企业债务融资工具不超过总资产的20%可表示为w2≤0.2174;

风险资产和无风险资产的投资收益率整理后如表3所示:

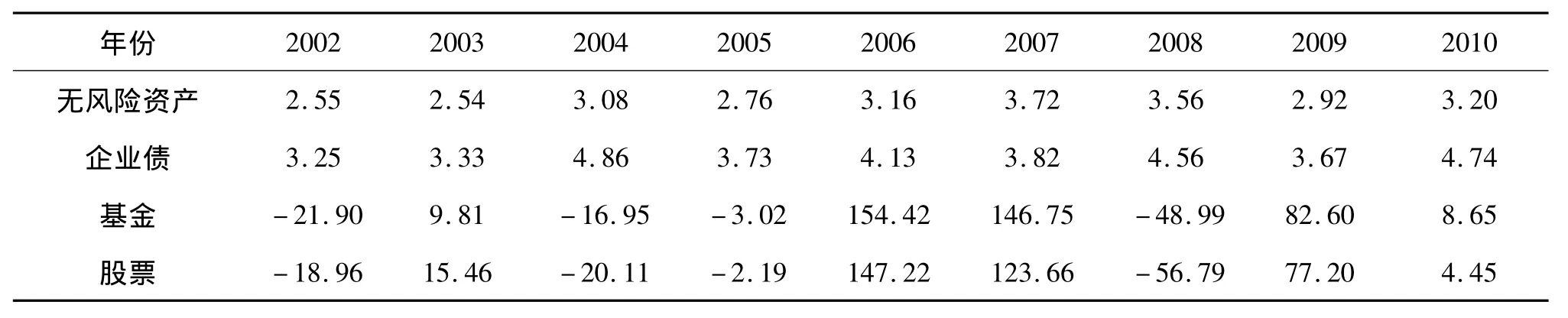
表3 保险公司各项资产的投资收益率 单位:%

风险资产收益率方差－协方差如表4所示:

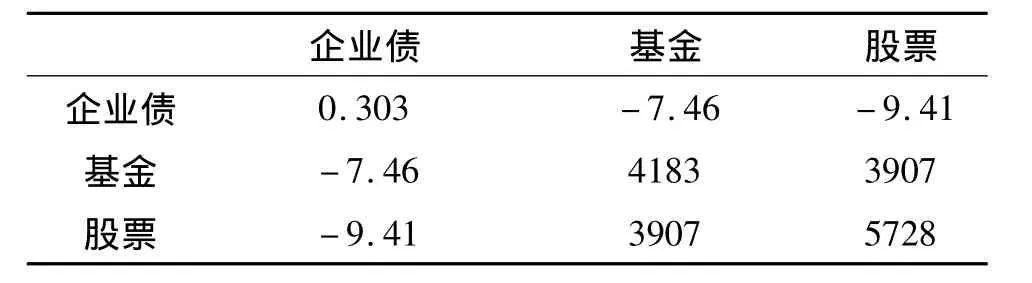
表4 方差-协方差矩阵

(2)模型计算

根据已经建立的模型和约束条件，最优化问题可表示为:

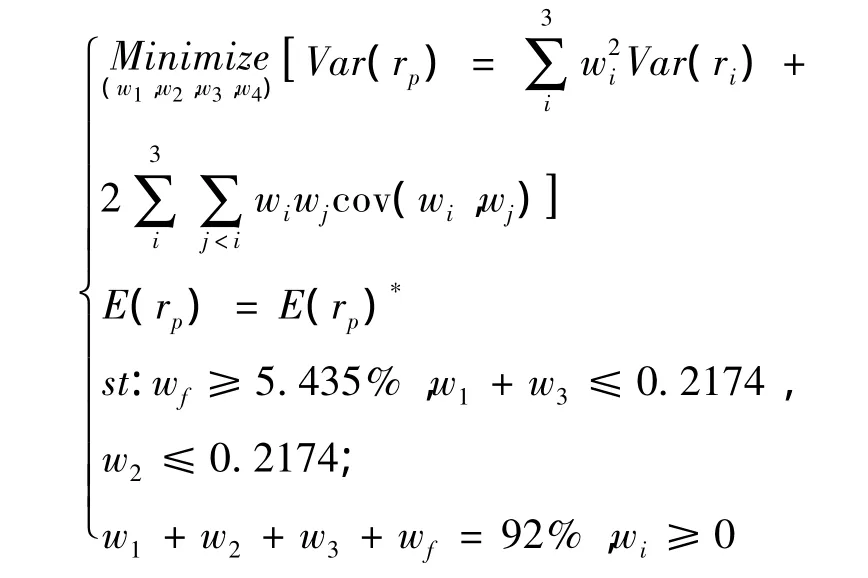
利用Lingo9.0对模型进行二次规划求解，可得出在各种给定投资收益率的情况下各种资产的配置比例关系及方差，结果如表5所示:

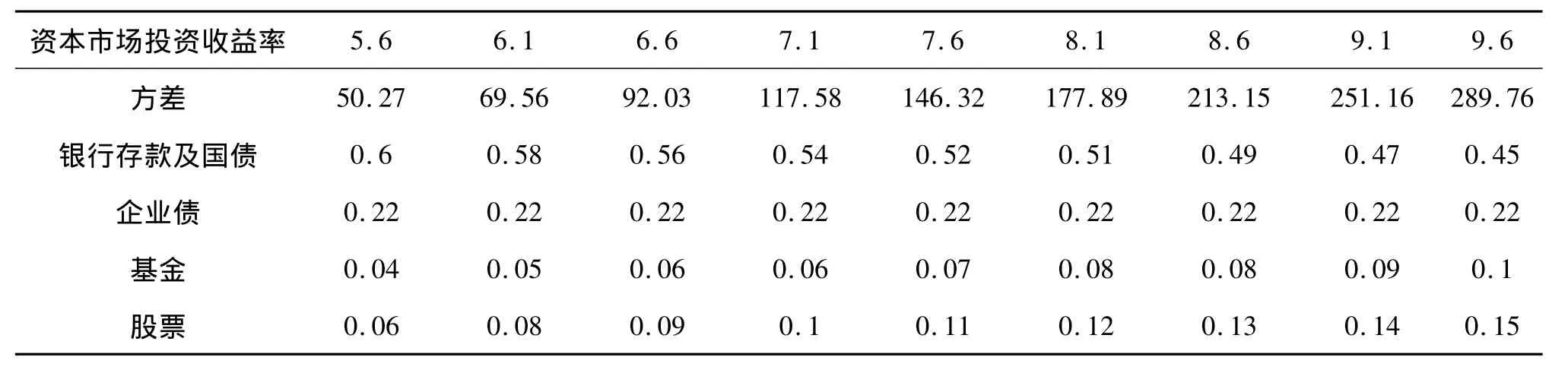
表5 二次规划结果

根据Markowitz投资组合理论，可以构造投资组合的有效边界，如图1所示:

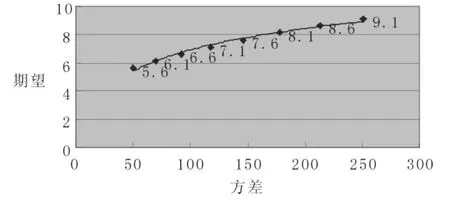
图1 投资组合有效边界

由此可知，最优投资组合应满足单位风险收益最大化，也即夏普比率(Sharpe ratio)最大。根据计算，当资本市场投资收益率为6.6%时，可得最优投资组合:银行存款及国债56%，企业债22%，证券投资基金6%，股票9%。而我国的保险资金实际投资比例如表6所示。

可以看出2009年的保险资金运用实际情况与我们计算的结果类似，总体上看，模型具有较好的理论基础和实践基础。

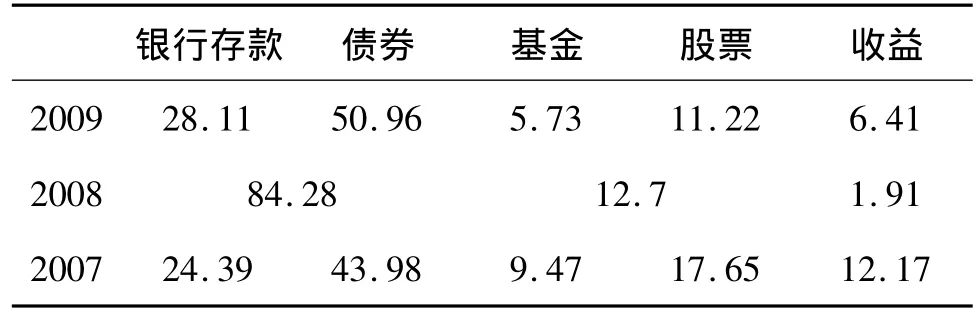
表6 我国保险资金投资比例 单位:%

五、对策与建议

1.加大我国保险资金投资资本市场的比例

从本文的实证分析可以看出，随着保险资金对股票和基金投资比例的增大，保险公司可以取得更高的投资收益。例如，本文的实证分析中保险资金最高可实现9.1%的收益，相应的投资组合为:银行存款与国债45%，企业债券22%，基金10%，股票15%。所以，我国保险公司应当适度增加保险资金在资本市场的投资比例，降低对银行存款的投资比例，从而取得较高的投资收益率，这样才能逐步缓解日益增加的承保压力。

2.进一步拓宽保险资金的投资渠道，探索新的投资工具

随着我国保险资金在资本市场的投资比例的增大，保险资金所承受的风险也必将相应增加。保监会应进一步放开保险资金投资渠道，使我国保险资金在取得较高收益率的同时，能够通过不同的投资工具达到分散风险的目的。本文得出的最优投资组合的收益率为6.6%，相应的方差为92.03。可见，即使在实现最优投资组合的情况下，我国保险资金仍面临较大的风险。笔者认为，我国保险资金应积极探索新的投资工具，例如金融衍生品，从而达到对冲风险的目的。

［1］J.David Cummins，David J.Nye.Portfolio Optimization Models for Property－Liability Insurance Companies［J］.Management Science，Vol.27，No.4，1981(4):414－430.

［2］Harry Markowitz.Portfolio Selection［J］.Journal of Finance，1952(7):77－91.

［3］Zvi Bodie，Alex Kane，Alan J.Marcus.Investment［M］(7th edition)，Chapter 7.

［4］Sharpe W F.A simplified model for portfolio analysis［J］.Management Science，1963(3):23－26.

［5］刘菲菲.Markowitz投资组合模型的遗传算法求解——在保险投资领域的实证研究［D］.青岛:中国海洋大学，2010.

［6］陈辉，陈建成.我国保险投资组合模拟和金融风险测量研究［J］.统计研究，2008(11):64－70.

［7］李冰清.保险投资［M］.天津:南开大学出版社，2007:98.

［8］郝佳.关于中国保险资金最优投资组合的实证研究［J］.海南金融，2007(10):26－32.