大跨度桥梁主梁风雨致涡激振动试验研究

辛大波，张明晶，王亮，欧进萍，2，李惠

(1.哈尔滨工业大学土木工程学院，黑龙江哈尔滨150090;2.大连理工大学土木水利学院，辽宁大连116024)

大跨桥梁是重要的基础设施工程.近年来，随着科学技术的进步以及经济的不断发展，大跨桥梁建设发展迅速，桥梁跨度不断增长，桥梁结构在自然风的作用下敏感度增加，风致颤振、抖振、涡激振动等典型风致振动成为影响大跨桥梁服役寿命的重要因素.涡激振动是大跨度桥梁在低风速下常见的一种风致振动现象，是一种带有自激振荡性质的风致限幅振动.尽管涡激振动不像颤振、驰振是发散的毁灭性的振动，但其对桥梁行车安全具有一定影响，并容易引起结构疲劳破坏［1］.长期以来，关于大跨桥梁涡激振动的研究都是基于桥梁处于均匀来流风场或紊流风场中，没有考虑降雨效应的影响.实际上，风和雨常常是同时存在的，特别是对于台风天气，强风和暴雨耦合更是其主要特征.大跨桥梁结构处于风雨联合作用时，单一考虑风场进行风致作用分析得出的结论与实际有一定的偏差，其原因在于雨场的存在以及雨场和风场之间的相互影响.因此，考虑降雨效应对桥梁风致作用的影响对于精确地分析大跨桥梁的最不利荷载环境以及准确地评价大跨桥梁涡激振动特性至关重要，且分析方法更符合客观实际.

目前，关于大跨桥梁风雨联合作用的研究主要集中在斜拉索风雨激振［2-12］，而针对大跨桥梁主梁风雨致涡激振动的研究还是空白.本文以某一分离式双箱主梁桥梁及其闭口主梁型式桥梁为研究对象，通过在哈尔滨工业大学闭口回流大气边界层风洞(湍流度小于3%，平均速度偏差小于5%)中安装降雨模拟装置进而搭建风雨联合作用环境试验系统，对桥梁风雨致涡振特性进行了试验研究.

1 涡激振动基本原理

当漩涡脱落频率接近结构某一阶自振频率时，将会引起涡激共振现象.Strouhal最先指出漩涡脱落现象可以用一个斯托罗哈数(Strouhal数)来描述:

式中:f是漩涡脱落一个完整的频率，Hz;D是物体垂直于平均流速的平面上的投影特征尺寸，m;U是来流的平均速度，m/s.

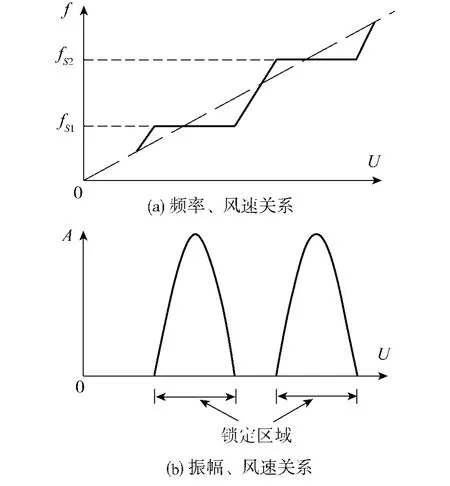
图1 涡激振动锁定现象Fig.1 The locking phenomenon of vortex induced vibration

当漩涡脱落频率接近于桥梁结构某一阶自振频率时，将引起桥梁结构较大的运动.桥梁结构和流体之间开始剧烈的相互作用，物体的固有频率控制了旋涡脱落现象，甚至当风速的变化使名义斯特罗哈频率已经偏离固有频率百分之几时，旋涡脱落仍被控制住.这种机械力对一种现象的控制通常称为锁定.锁定对旋涡脱落的影响见图1.

2 风雨联合作用下桥梁主梁涡激振动试验

2.1 试验环境及试验系统

试验在哈尔滨工业大学风洞与浪槽联合实验室完成.通过在闭口回流大气边界层风洞中安装降雨系统，进而实现风雨联合作用环境，整个风雨联合作用系统还包括实验装置、测试系统、数据采集系统、挡雨防水装置、排水管道、进风口以及出风口.试验段风雨联合作用环境如图2所示.

图2 风雨联合作用环境Fig.2 Surroundings of simultaneous actions of wind and rain

如图2所示，风雨联合作用降雨系统包括3个进水管以及15个喷水管，降雨系统模拟雨强连续变化范围10～200 mm/h，降雨影响面积4×5 m2，雨滴直径0.1～6 mm，降雨调节精度7 mm/h.节段模型的两端用螺栓连接到试验框架上，并由弹簧系统支撑，弹簧系统竖向刚度为10 N/mm.试验使用3个DeltaTron®Type 4507 B加速度计，分别测量加速度计最大量程为±700 m·s－2，为了防水，在加速度计贴防水保护膜一层.本试验给定的雨强分别为0、30、60、90、120、150、180 mm/h.

2.2 试验模型

试验选取某一分离式双箱悬索桥为研究对象.试验采用的节段模型缩尺比为1∶40，同时为了方便进行对比研究，试验还增加了针对该悬索桥节段模型开孔槽的闭口模型，2个模型具有相同的外轮廓尺寸，节段模型采用轻质木材制作，模型质量约16 kg.开口主梁节段模型和闭口节段模型分别如图3、4所示.

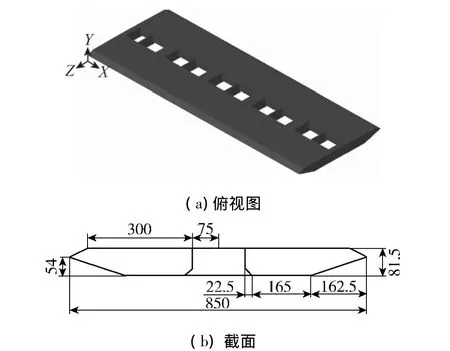
图3 开口主梁节段模型Fig.3 Slotted section model

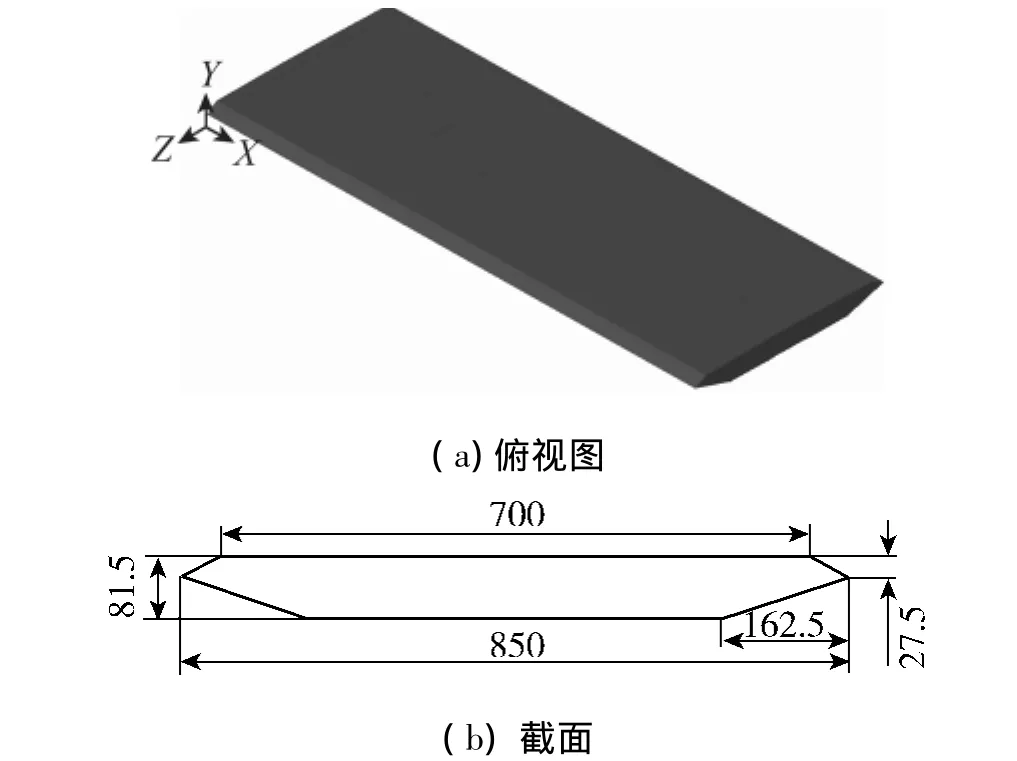
图4 闭口节段模型Fig.4 Closed section model

本试验针对开口闭口2个主梁节段模型的主要结构参数如下表1所示.

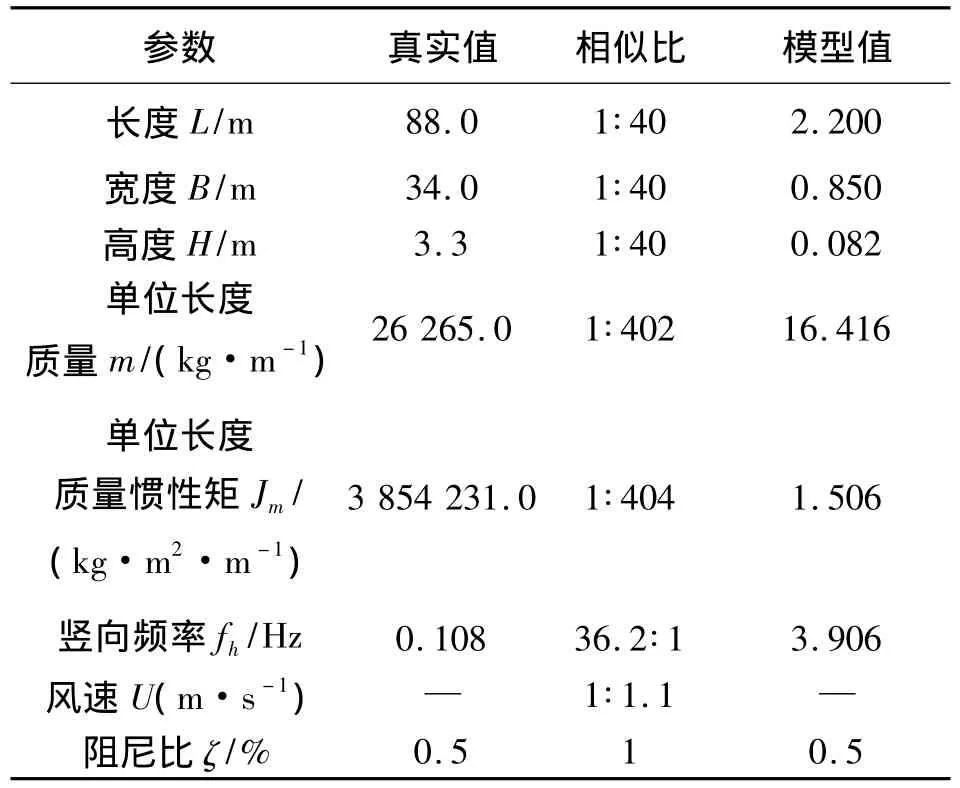
表1 节段模型系统的主要参数Table 1 Parameters of the section model system

3 风雨联合作用下涡激振动试验结果与分析

3.1 振动时程

在不同雨强作用下，通过加速度传感器获得开、闭口节段模型加速度时程曲线如图5所示.图5(a)中，0～2 s、2～4 s、4～6 s、6～8 s、8～10 s分别对应的来流风速为1.6、1.8、2.0、2.2、2.4 m/s.图5 (b)中，0～2 s、2～4 s、4～6 s、6～8 s、10～12 s分别对应的来流风速为2.0、4.2、4.8、6.0、7.6、9.3 m/s.

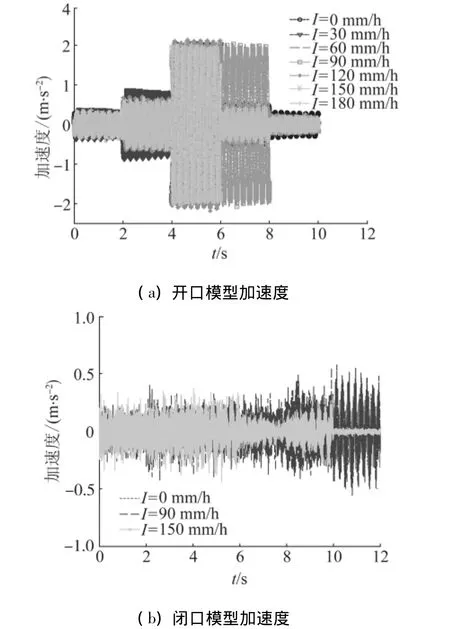
图5 开、闭口模型加速度时程Fig.5 Acceleration time histories for the slotted model and the closed model

由图5可知，开口节段模型产生了明显的涡激振动.不同雨强下，起振风速及锁定风速基本一致.不同雨强下，最大加速度峰值有一定差别.闭口节段模型产生的是随机振动，且随着风速增大，加速度峰值增大.不同雨强下，闭口节段模型加速度振动时程有一定差别.试验表明开、闭口节段模型在抵抗涡激振动方面差别显著，当气流流过所开的凹槽时，会产生较大的漩涡脱落，加剧了模型来流尾部的漩涡脱落.

对图5中的开、闭口节段模型的加速度时程进行频域积分得到各自相应的位移时程.不同雨强作用下，开、闭口节段模型位移时程曲线如图6所示.图6(a)中，0～2 s、2～4 s、4～6 s、6～8 s、8～10 s，分别对应的来流风速为1.6、1.8、2.0、2.2、2.4 m/s.图6(b)中，0～2 s、2～4 s、4～6 s、6～8 s、8～10 s、10～12 s分别对应的来流风速为2.0、4.2、4.8、6.0、7.6、9.3 m/s.

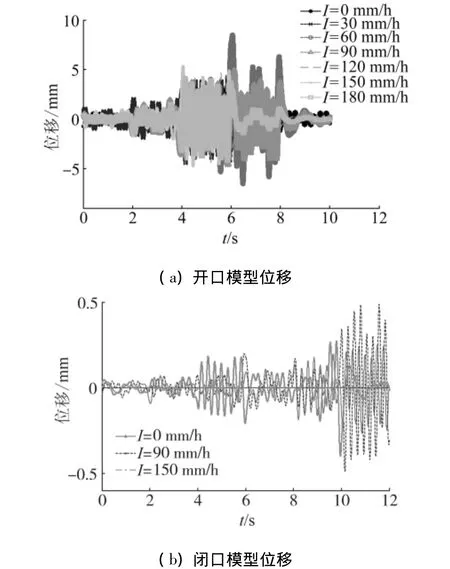
图6 开、闭口模型振动时程Fig.6 Displacement time histories for the slotted model and the closed model

由图6可以看出，开口节段模型产生了明显的涡激振动.不同雨强下，最大位移峰值有一定差别.闭口节段模型产生的是随机振动，且随着风速增大，位移峰值增大.不同雨强下，闭口节段模型位移振动时程有一定差别.

3.2 功率谱密度

通过对图5振动加速度时程反应进行傅里叶变换，可以得到不同雨强作用下的桥梁主梁节段模型的功率谱特性曲线.开、闭口节段模型的功率谱密度如图7所示.

由图7可以看出，对于开口节段模型，不同雨强作用下，功率谱特性曲线有一定差别，在频率为3.9 Hz时，各条曲线达到最大值.功率最大值可达0.86 dB.对于闭口节段模型，不同雨强作用下，功率谱特性曲线有一定差别，在频率为3.9 Hz附近时，各条曲线达到最大值.功率最大值为0.22 dB.通过对开、闭口节段模型功率谱特性曲线峰值大小比较，表明闭口模型相对于开口模型具有较低的振动能量.

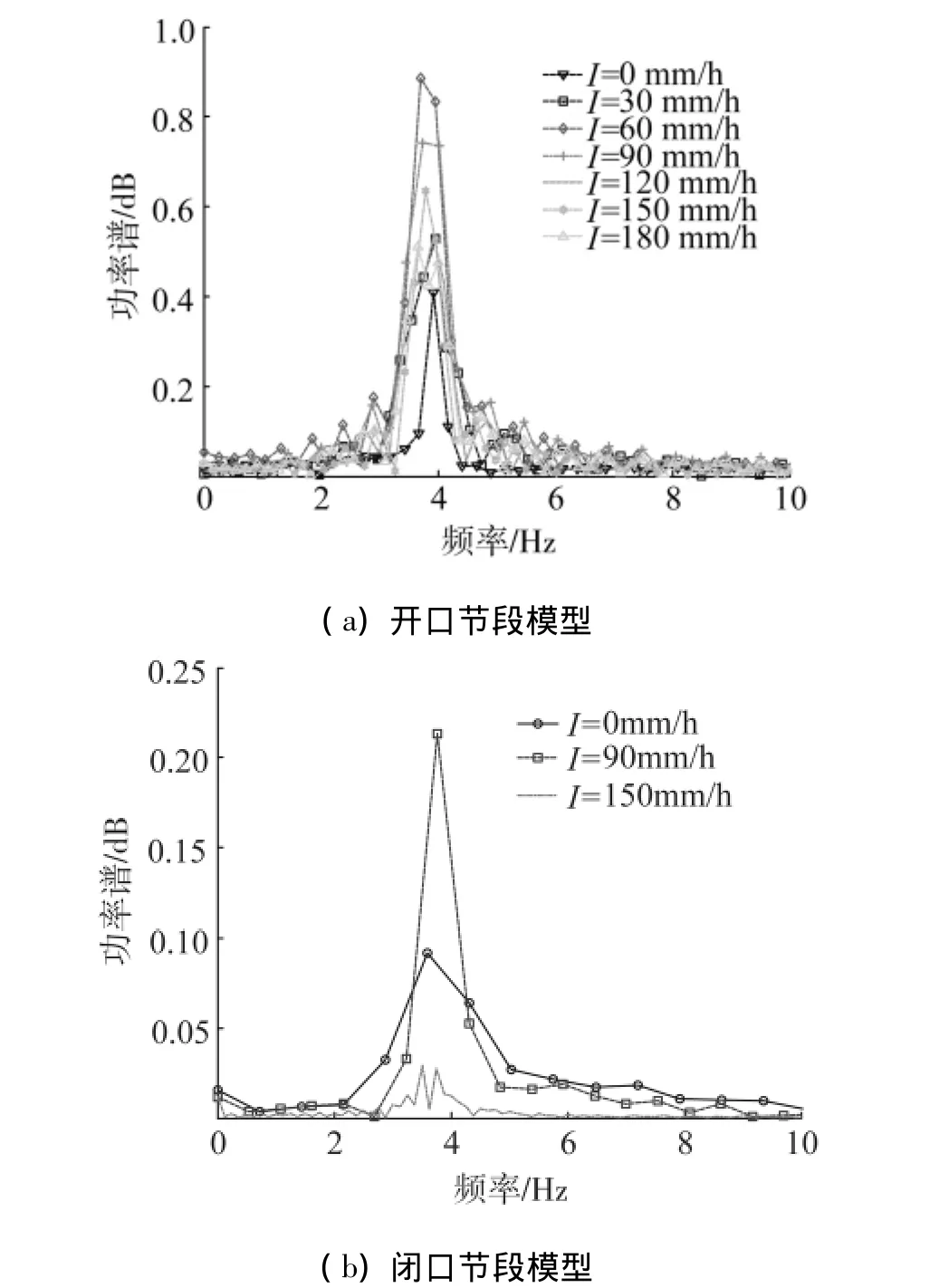
图7 开、闭口节段模型功率谱密度Fig.7 Power spectral density for the slotted model and the closed model

3.3 位移幅值

不同的风速作用下，可以得到不同的模型振动幅值.在雨强为150 mm/h时，不同风速下开、闭口模型振动位移幅值如图8所示.

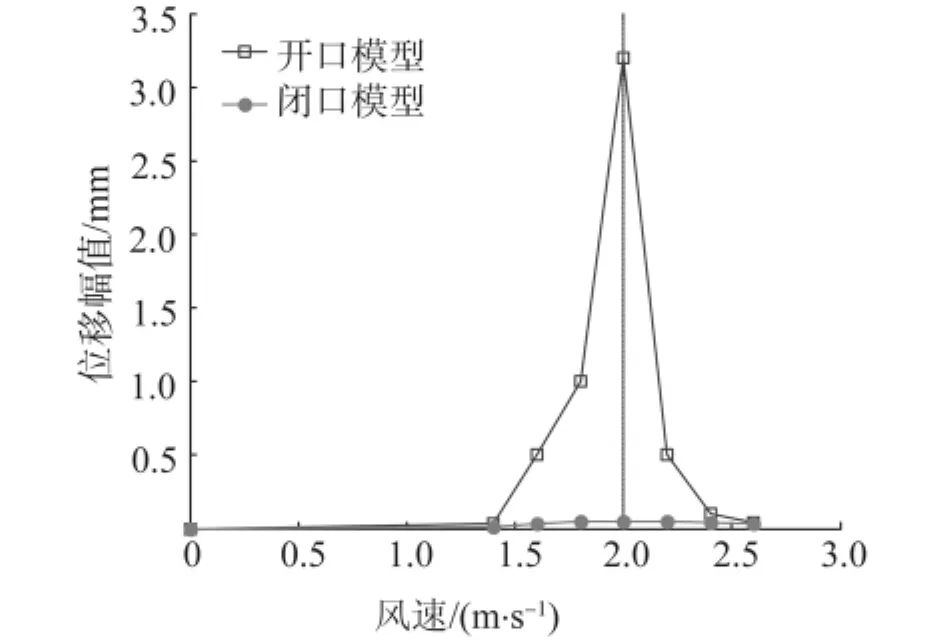
图8 位移幅值随风速变化Fig.8 Displacement amplitude changing with wind velocity

由图8可以看出，开口节段模型的起振风速为1.4 m/s，锁定风速区间为1.4～2.5 m/s.最大涡激振动幅值为3.25 mm.闭口节段模型振动幅值较小.这表明涡激振动对于气动外形的敏感性非常强，在抵抗涡激振动方面，闭口节段模型相对于开口节段模型有着较为优良的性能.

针对开口节段模型不同雨强下的涡激振动最大位移幅值如图9所示.

图9 开口模型最大位移幅值Fig.9 Displacement amplitude for the slotted model in different rainfall intensity

由图9可知，不同雨强下，开口节段模型的涡激振动位移幅值有一定差别.相对于纯风作用，开口节段模型在风雨联合作用下的最大位移幅值较大，最大增量可达25%.当雨滴降落到桥梁节段的表面上，经过冲击、飞溅、流动等过程，雨水会形成对应于桥梁节段结构条件的一种特定形态，比如桥梁节段表面的水膜.水膜的振动将会产生很大的附加空气动力作用，这也是涡激振动幅值提高的原因所在.表明风雨致涡激振动要比风致涡激振动危险，考虑降雨作用下的涡激振动显得十分必要.

4 结论

本文通过在大气边界层风洞中安装人工模拟降雨器进而搭建风雨联合作用试验系统，针对某一分离式双箱桥梁主梁节段模型以及其闭口型式的节段模型，进行了不同雨强作用下的桥梁节段模型涡激振动试验，获取桥梁主梁断面涡激振动特性，通过分析相关试验结果，得出以下结论:

1)开口节段模型产生了明显的涡激振动.不同雨强下，起振风速及锁定风速基本一致.不同雨强下，最大振动幅值有一定差别.闭口节段模型产生的是随机振动，且随着风速增大，振动幅值增大.不同雨强下，闭口节段模型振动时程有一定差别.

2)开口节段模型在风雨联合作用下的位移幅值大于其在单一风作用下的位移幅值，最大增量可达四分之一.说明风雨致涡激振动要比单一风致涡激振动危险，考虑降雨作用下的涡激振动显得十分必要.

3)涡激振动对于气动外形的敏感性非常强，在抵抗涡激振动方面，闭口节段模型相对于开口节段模型有着较为优良的性能.

［1］陈政清.桥梁风工程［M］.北京:人民交通出版社，2005: 129-136.CHEN Zhenqing.Bridge wind engineering［M］.Beijing: China Communications Press，2005:129-136.

［2］BLOCKEN B，CARMELIET J.High-resolution wind-driven rain measurements on a low-rise building experimental data for model development and model validation［J］.Journal of Wind Engineering and Industrial Aerodynamics，2005(93):905-928.

［3］BLOCKEN B，CARMELIET J.On the accuracy of winddriven rain measurements on buildings［J］.Building and Environment，2006(41):1798-l810.

［4］BLOCKEN B，CARMELIET J.Guidelines for the required time resolution of meteorological input data for wind-driven rain calculations on buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008(93):621-639.

［5］WIANECHI J.Cable wind excited vibrations of cable-stayed bridge［M］.［s.l.］.1979.

［6］MATSUMOTO M，SHIRASHI N，SHIRATO H.Rain-windinduced vibration of cables of cable-stayed bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992(41-42):2011-2022.

［7］BOSDOGIANNI A，OLIVER D.Wind and rain induced oscillations of cables of stayed bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1996(64):171-185.

［8］GU M，DU X Q.Experimental investigation of rain-wind-induced vibration of cables in cable-stayed bridges and its mitigation［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003(93):79-95.

［9］MAIN J A，JONES N P.Full-scale measurements of stay cable vibration［C］//Proceedings of 10th Conference on Wind Engineering.Rotterdam，The Netherlands，1999:963-970.

［10］NI Y Q，WANG L Y，CHEN Z Q，KO J M.Field observations of rain-wind-induced cable vibration in cable-stayed Dongting Lake Bridge［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007(95):303-328.

［11］XU Y L，WANG L Y.Analytical study of wind-rain induced cable vibration:SDOF model［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003(91):27-40.

［12］LI H，LIU M，LI J H，et al.Vibration control of stay cables of the Shandong Binzhou Yellow River highway bridge by using magnetorheological fluid dampers［J］.Journal of Bridge Engineering，2007，12(4):401-409.