运用希尔伯特黄变换进行多分量信号的频散分析

蒋 礼

(1.中国地质大学地球物理与空间信息学院,武汉 430074;2.华北水利水电学院数学与信息科学学院,郑州 450011)

1 引 言

传统面波的频散分析方法主要分为谱分析法(SASW)[1]和多道分析法(MASW)[2]两类。虽然SASW具有原理简单、运算速度快等优点,但由于下列两个主要原因的影响导致该算法的准确性远低于MASW。第一,无论是用时差还是相差来提取群速度或相速度,由于时差和相差都是位于分母,故而任何细微误差都会对求取的速度造成很大的影响;第二,谱分析所得到的相位并非该信号的真实相位,故而存在相位解缠的难题。

本文首先将希尔伯特黄变换应用于时频分析,从而获得比传统傅里叶谱更为精确的希尔伯特谱,进而得到较为准确的群速度信息;然后,依据群速度和相速度的关系,提出在群速度的基础上求取相速度的新算法,该算法可以有效地解决相位解缠难题,并能最终获得较为准确的相速度信息。

2 原理简介

通常有3类方法进行时频分析:基于时频窗类的短时傅里叶变换、gabor变换和小波变换[3];基于相关性研究的Cohen类时频分布[3];基于瞬时频率的希尔伯特谱分析[3,4]。希尔伯特谱不受时频不确定原理的限制,故该谱比傅里叶谱有着更精确的时频刻画能力;而且希尔伯特谱也不必顾虑类似于Cohen类时频分布交叉项、边缘条件等核干扰的问题,故该谱比Cohen分布更接近于该信号的真实物理频率(即傅里叶频率)。

2.1 希尔伯特黄变换

2.1.1 瞬时频率

[3]

设某实信号 s(t)=A(t)ejφ(t),其中 A(t)表示瞬时幅度,φ(t)表示瞬时相位,其解析信号的傅里叶变换结果为S(ω),则其平均频率为

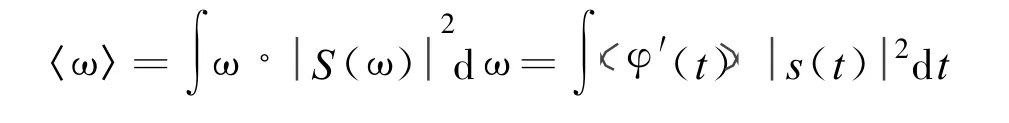
因此瞬时频率为

由式(1)可知,瞬时频率即为某一时刻的平均频率,如果该信号为单分量信号,则 φ/(t)即为真实的物理频率(即傅里叶频率)。

2.1.2 经验模态分解(EMD)

将一个多分量信号分解为一系列单分量信号之和的过程称之为经验模态分解[5,6],每一个单分量信号称为一个固有模态函数(IMF)。

对实信号s(t)进行经验模态分解可得:

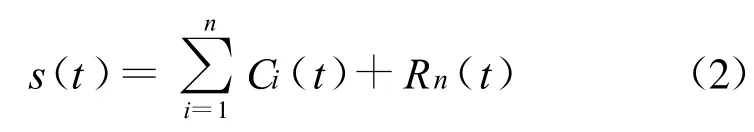
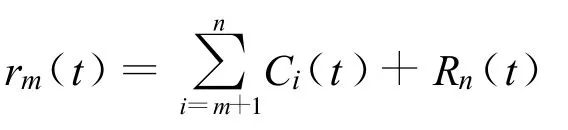
2.1.3 希尔伯特谱

对于各单分量信号,利用希尔伯特变换(HT)可以得到基于瞬时频率的希尔伯特谱。希尔伯特谱H(t,ω)主要有两类,即时间-频率-能量谱He(t,ω)和时间-频率-相位谱Hp(t,ω),从这两类谱中可以获得时间、频率、能量和相位的分布关系。

希尔伯特黄变换的完整算法流程如下:

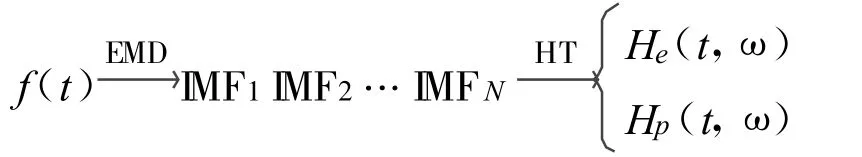
2.2 频散分析

以地震波信号为例,设震源的单分量信号[1]为s(t)=A(t)ejφ(t),道间距(即相邻检波器的距离)为Δx,某道的该分量信号为

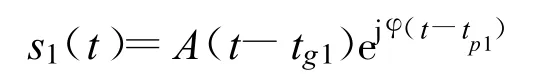
相邻道的该分量变为

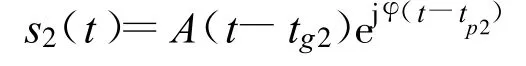
式中,tg为群传播的时差,tp为相传播的时差,则群速度 Vg=Δx/(tg2-tg1),相速度Vp=Δx/(tp2-tp1)。

2.2.1 群速度

时频能量谱He(t,ω)为传统的时频分析谱,从中可以获得各分量信号的能量分布情况和群速度计算结果[7]。

tg为群传播时差,即能量传播的时差。根据时频谱He(t,ω),某单分量信号IMFn的能量传播时差为

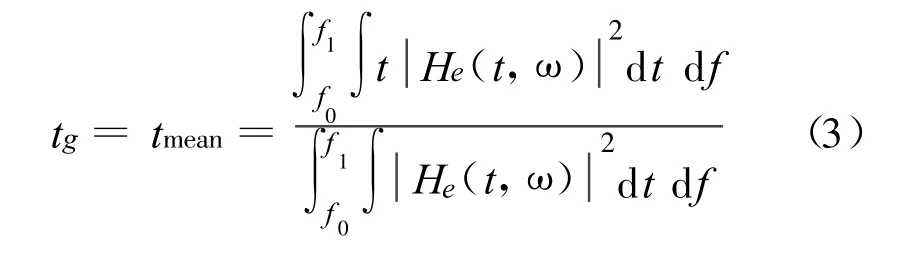
而该单分量信号的傅里叶频率即平均频率为

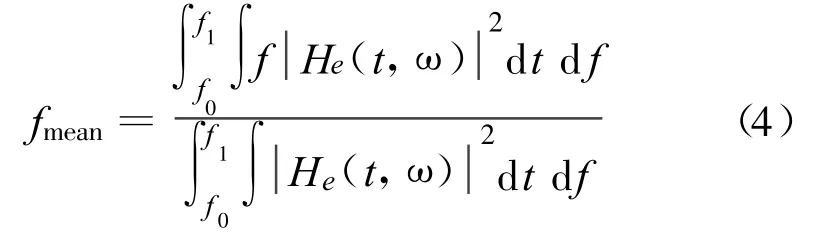
该单分量信号的振幅计算公式为

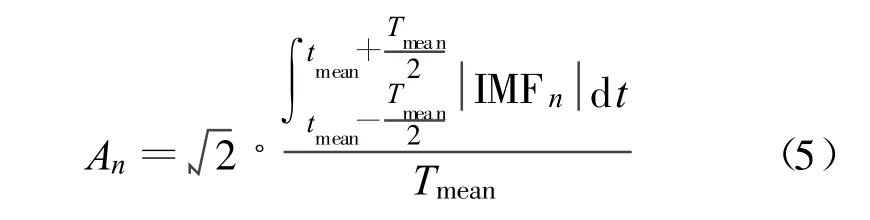
式中,f0、f1分别为该单分量信号瞬时频率的起、止频率,Tmean=1/fmean为该单分量信号的周期。

2.2.2 相速度

从时频相位谱Hp(t,ω)中可以获得各分量信号在任意时刻的瞬时相位,再根据相差计算公式可以求取各分量信号的相速度。

(1)同步相差[1,8],即同时在两道检波器获取同一分量检测信号的相位差。

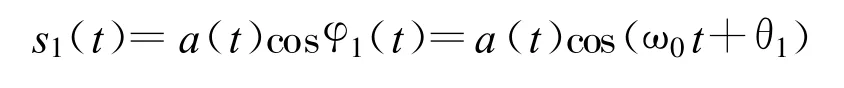
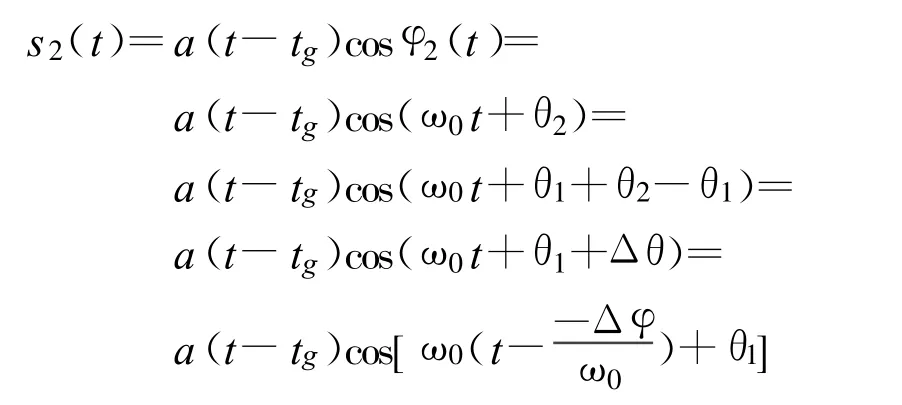
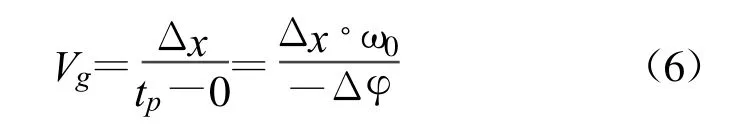
式中,Δφ为同步相位差,Δx为道间距。

由于低频信号周期较长,因此前后两道同时检测到该信号的相位值(相位值的取值范围在±2π内)依然有可能位于同一周期内,此时并不需要进行相位解缠;而中频和高频信号因为周期较短,所以前后两道同时检测到该信号的相位值很有可能已不在同一周期内,此时必须进行相位解缠,才能获得真实的相位差。

(2)异步相差,即相邻两道检波器在不同时刻所得同一分量信号的相位差。

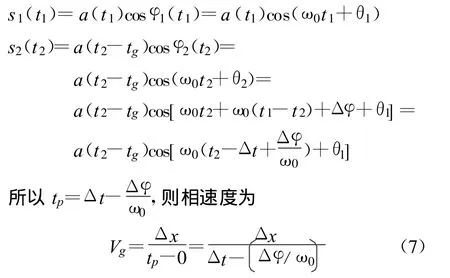
式中,Δφ为异步相位差。

假设沿着波的传播方向,先到达的检波器记录下某分量信号某一时刻的相位,后到达的检波器记录下该分量信号略微延迟一下的相位,只要检测时差控制得当,任何频率的相位差都可控制在同一周期内,所以使用恰当时差的异步相差完全可以避免相位解缠。

(3)校正相差,即利用群速度传播时差代替估计时差的异步相差。

虽然使用恰当时差的异步相差可以完全避免相位解缠,但测量时差的选取只能进行估计尝试。一旦该时差的选择出现少许偏差,由于中频、高频信号周期较短,此时依然会面临相位解缠;如果时差选择反了,有可能低频信号也要进行相位解缠,而中高频信号将面临着更复杂的相位解缠。对于地球物理勘探常用的瑞利面波信号而言,各频率信号的群速度和相速度的变化规律基本一致(随着频率的增加而减小),故各分量的群传播时差和相传播时差的区别通常不会太大。

校正相差为

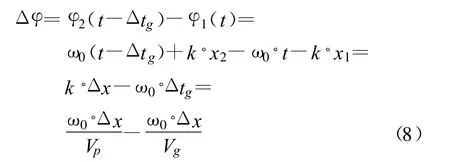
式中,k为波数。若Vp与Vg相近,则Δφ可控制在±2π内,此时可以避免相位解缠,将式(8)计算结果直接代入式(7)即可求出相速度。校正相差可以有效解决估计时差问题,并且可以在一定程度上避免相位解缠。

3 仿真实例

3.1 模型建立

设某个瑞利波源是由3个单分量信号组合而成,各分量的具体参数详见表1。从该表中可以看出该模拟波低频分量能量大、高频分量能量小,各分量信号的群速度和相速度随着频率的增加而减小,且群速度小于相速度,这些特征十分符合地震瑞利面波特性。

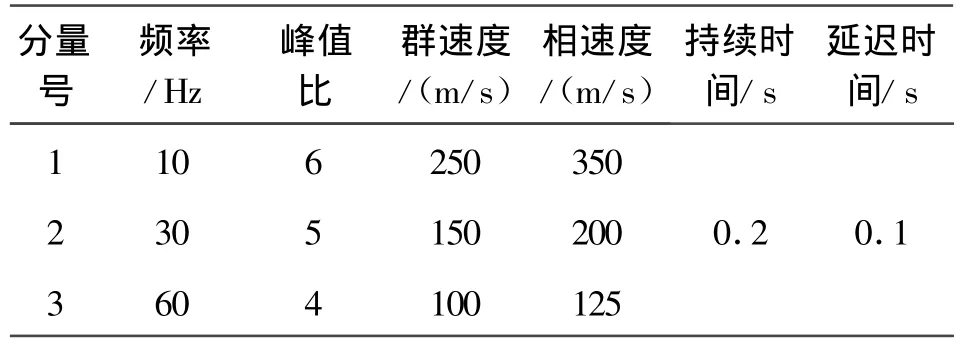
表1 瑞利波源分量参数列表Table 1 Rayleigh wave source component parameter list

两个检波器分别距离震源12 m和18 m,检波时间为1.023 s,采样时间间隔为1ms。12 m处检波器所得信号如图1(a)所示,18 m处的信号如图1(b)所示。从图中可以看出,信号所占时宽随着传播距离增加正在慢慢变大,各分量信号在传播过程中因速度不同正在互相分离,这是典型的频散效果。对这两个信号进行希尔伯特黄变换,并绘制出相应的时间-频率-能量谱(如图 1(c)、(d)所示)和时间-频率-相位谱(如图1(e)、(f)所示)。

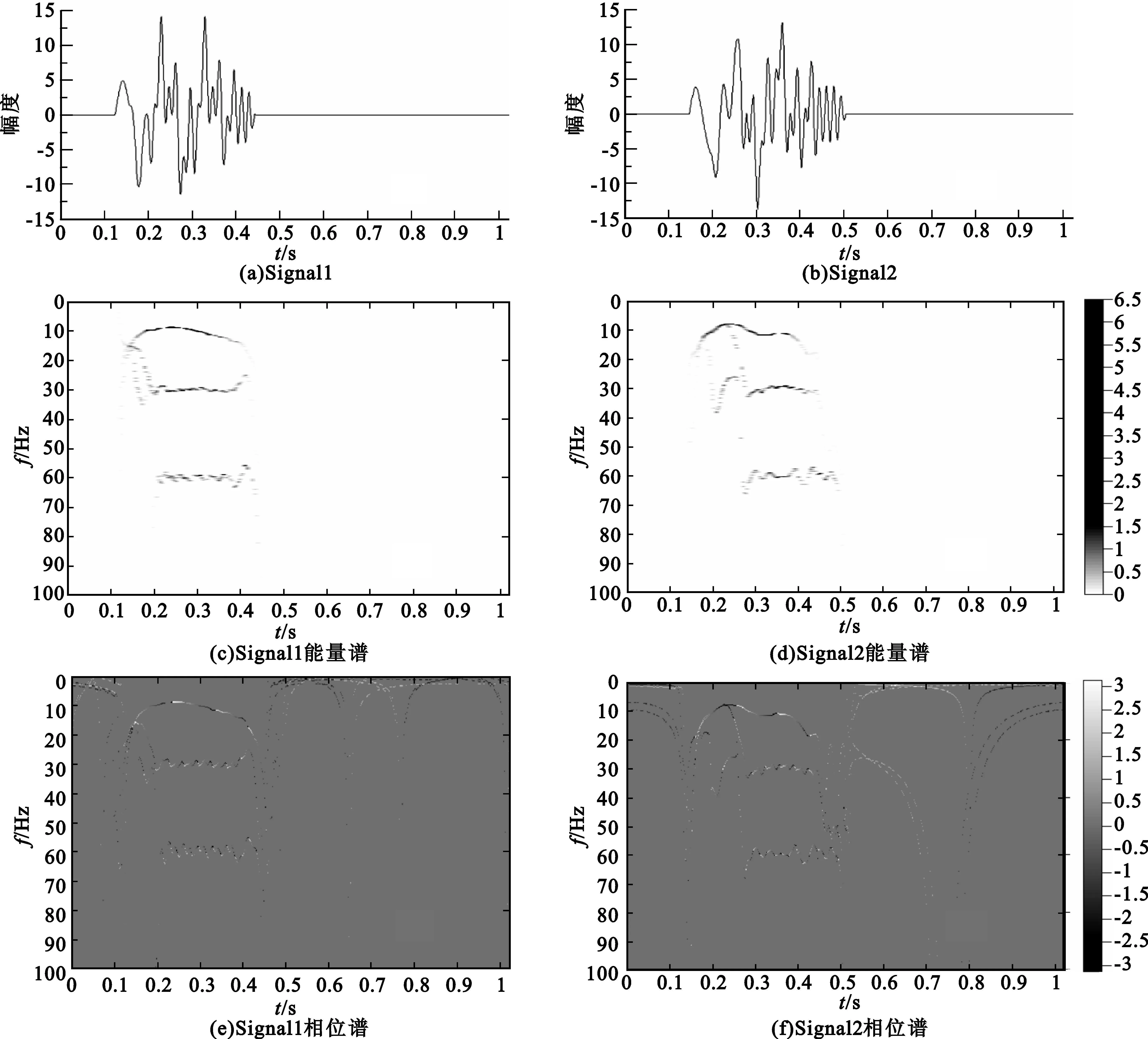
图1 希尔伯特黄变换谱分析图Fig.1 Spectrum analysis diagram of the Hilbert-Huang transform

3.2 希尔伯特谱分析

3.2.1 相位谱和能量谱

时间-频率-能量谱简称能量谱,从图1(c)和图1(d)中可以看出该谱横轴为时间轴,纵轴为频率轴,色标代表着多点平滑幅值也即能量。该图可以看作是传统的时频分析图,只不过此图的频率为瞬时频率;时间-频率-相位谱简称相位谱,该谱与能量谱类似(见图1(e)和图1(f)),横轴为时间轴,纵轴为频率轴,但色标代表着相位。

从相位谱和能量谱的对比可以看出,不是所有的瞬时相位都有意义。对于某一单分量信号而言,有能量的相位或者能量大于某一设定阈值的相位,可看作是该分量信号的真实相位;而其余的相位可看作是能量泄漏在该频段产生的干扰相位,这部分相位没有真实的物理意义。对于同一信号使用不同的EMD方法可能会出现不同的干扰相位,但真实相位始终相同。

无论从能量谱还是相位谱中我们都可以清楚地看到3个单分量信号的信息,各分量的瞬时频率非常接近于真实的物理频率,起止时间、持续时间和能量分布也基本正确。为了分析相位谱的正确性,将图1(e)的各分量单独提出,并与理论值进行比较,如图2所示。图2(a)、(b)、(c)为三分量信号的时域波形,图2(d)、(e)、(f)为根据理论计算绘制出的真实时频相位图,图2(g)、(h)、(i)为图1(e)的各分量单独的时频相位图。从图2中各相应分量逐一对比可以发现,相位谱的瞬时相位十分准确,频率虽有所误差但基本在正确频率值附近扰动。

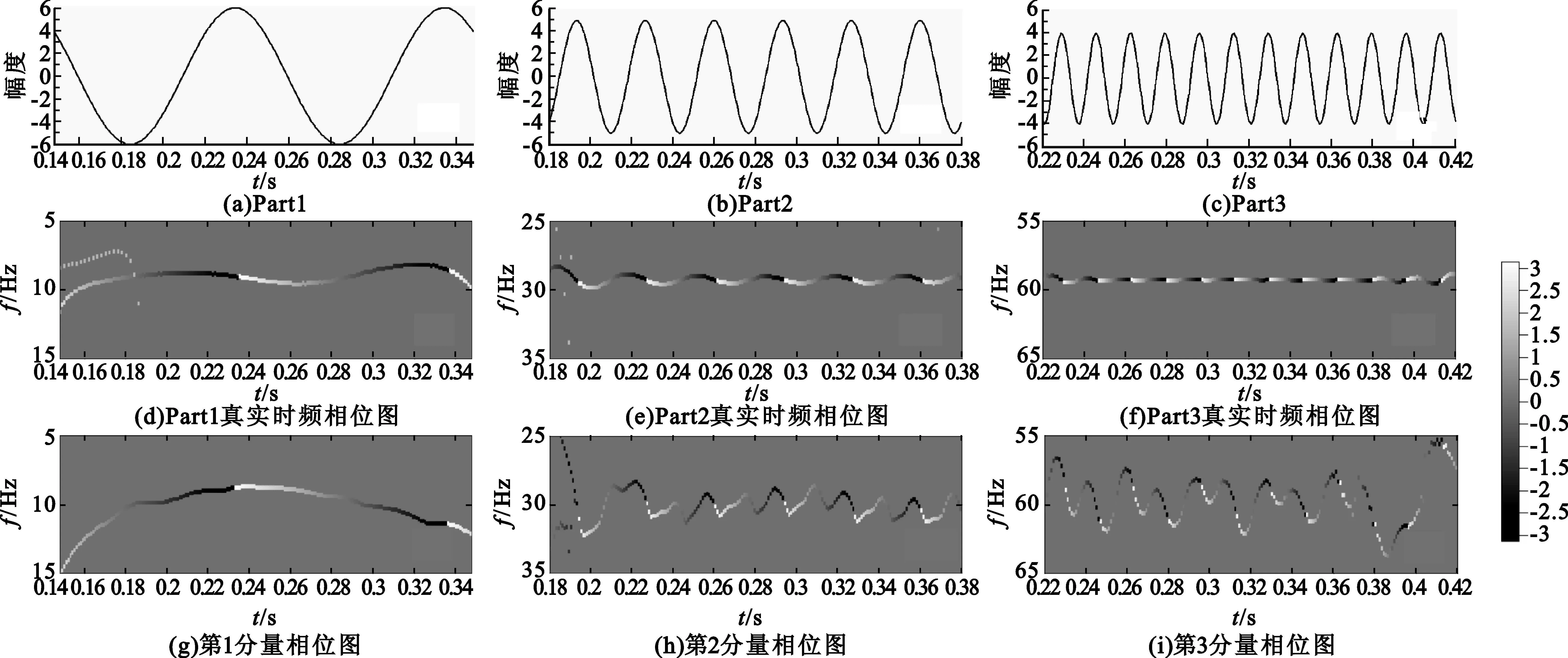
图2 单分量信号的相位谱分析图Fig.2 Phase spectrum analysis diagram of the single-component signal

3.2.2 相位解缠

由于我们所实测的相位值在±2π内,如果同一分量信号在两个相邻检波器所测量的相位并不是位于同一周期内的,那么此时的相位之差并不能反映真正物理意义上的相差,这种情况下必须要进行相位解缠。

以第二分量信号为例,将图1(e)和图1(f)中的该分量信号提取出来,即以该分量信号能量中心为中心点,截取相邻两道该分量信号相同大小的相位谱图(如图3所示)。从图3中可以发现,两幅图所共同覆盖的时间内任意一个时刻信号的相位差,除了实测相位之差外还应该加上一个周期的补偿。那么对于该分量信号而言,真实相位差等于实测相位差加2π。

3.3 结果分析

3.3.1 能量分布及群速度

利用能量谱和式(3)～(5)可以获得各分量信号的频率、振幅以及群速度。表2所示为平均频率与能量分布。

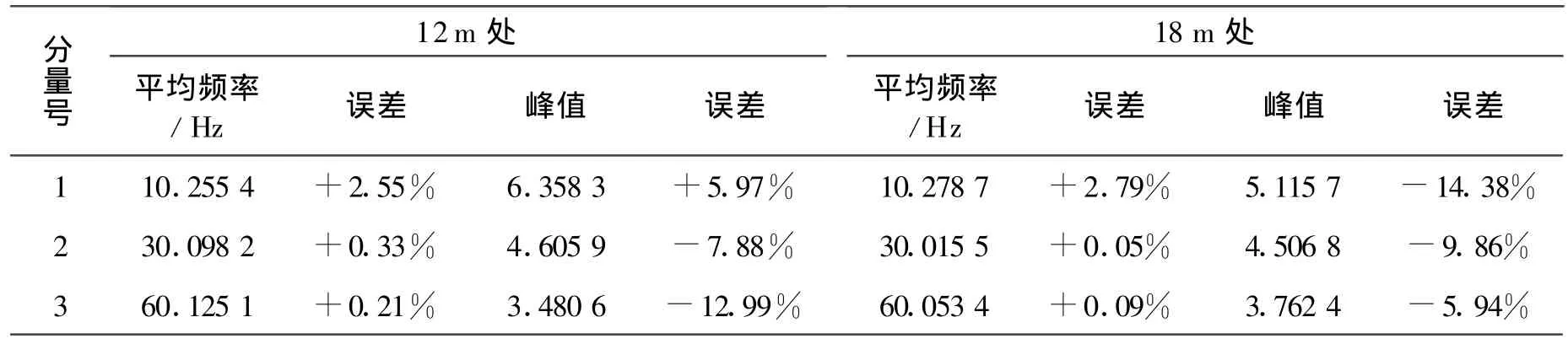
表2 平均频率与能量分布Table 2 Average frequency and energy distribution

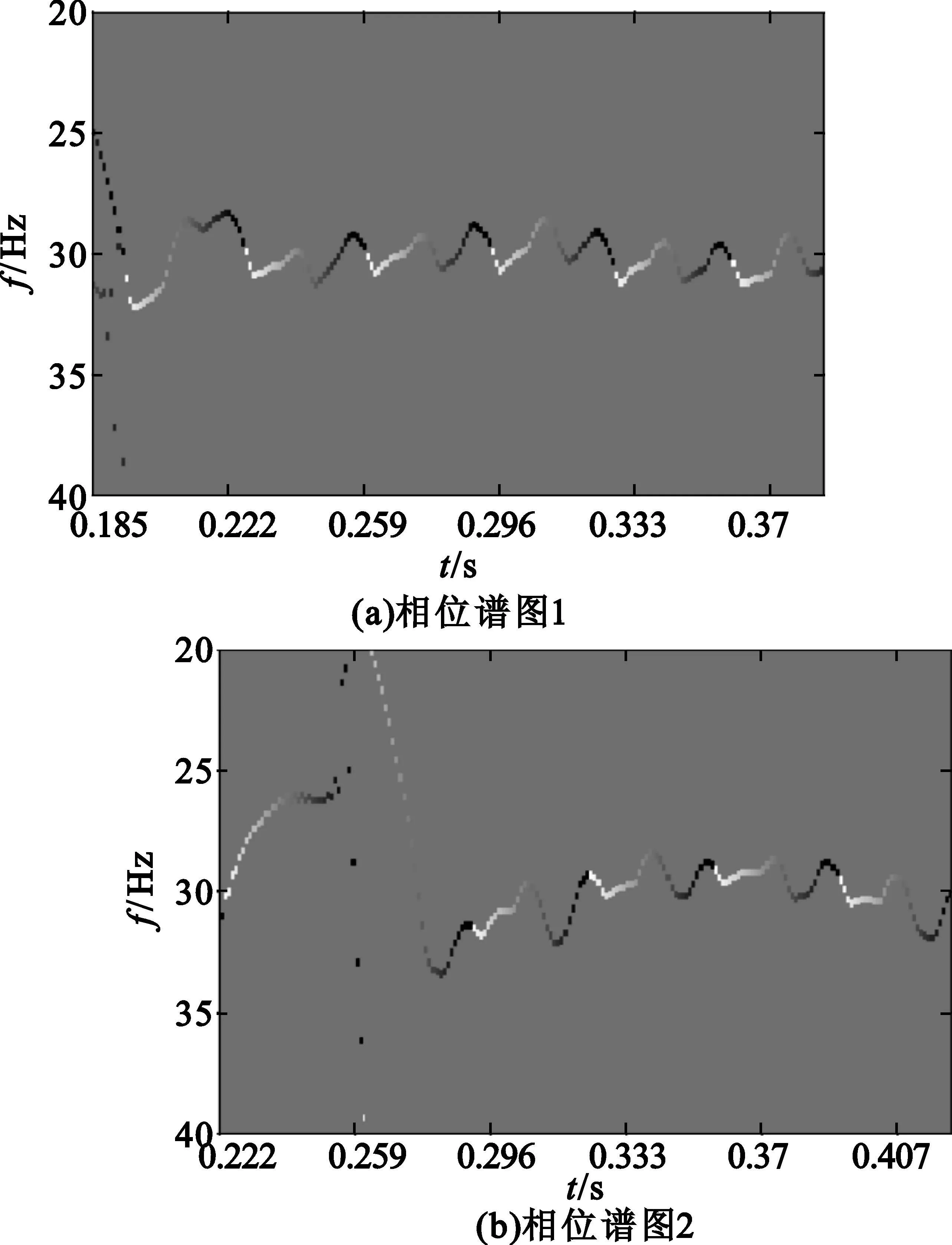
图3 相位解缠图Fig.3 Phase unwrapping diagram

从表2中可以看出,各分量信号的频率值非常准确,但各分量的振幅值误差较大,且绝大多数振幅值都偏小,这是由于EMD分解过程中能量泄漏所造成的。群速度计算结果及其误差如表3所示。

表3 群速度计算结果及其误差Table 3 Group velocity and error

从表3中可以看出,无论是时间还是群速度的计算结果都非常准确。

3.3.2 相速度

从图1(c)和图1(d)中可以看出,各分量信号都经过0.3 s,即无论是在12 m处还是18 m处,0.3 s时的信号包含各分量的信息。依据同步相差的原理可以选择12 m处和18 m处在0.3 s时的瞬时相位计算各分量的相速度。

根据公式(6)可以计算出各分量的相速度,从相位谱中可以看出,低频分量不用进行相位解缠;中频分量和高频分量则需要在所求相差的基础上增补一个周期2π和3个周期6π,才能求出真实相差。计算结果如表4所示。

表4 同步相差计算相速度Table 4 Phase velocity with synchronous phase difference

从图1(d)中可以看出,各分量信号都经过0.35 s,即在18 m处0.35 s时的信号包含各分量的信息。依据异步相差的原理可以选择12 m处在0.3 s时的瞬时相位和18 m处在0.35 s时的瞬时相位计算各分量的相速度。

由于检测时差选择合适,低、中、高频分量信号皆不用进行相位解缠。依据公式(7)的计算结果如表5所示。

表5 异步相差计算相速度Table 5 Phase velocity with asynchronous phase difference

利用表3各分量的群速度求出该分量在相邻检波器间的传播时差,并将该时差代入公式(7)即可求出该分量的相速度,计算结果见表6。

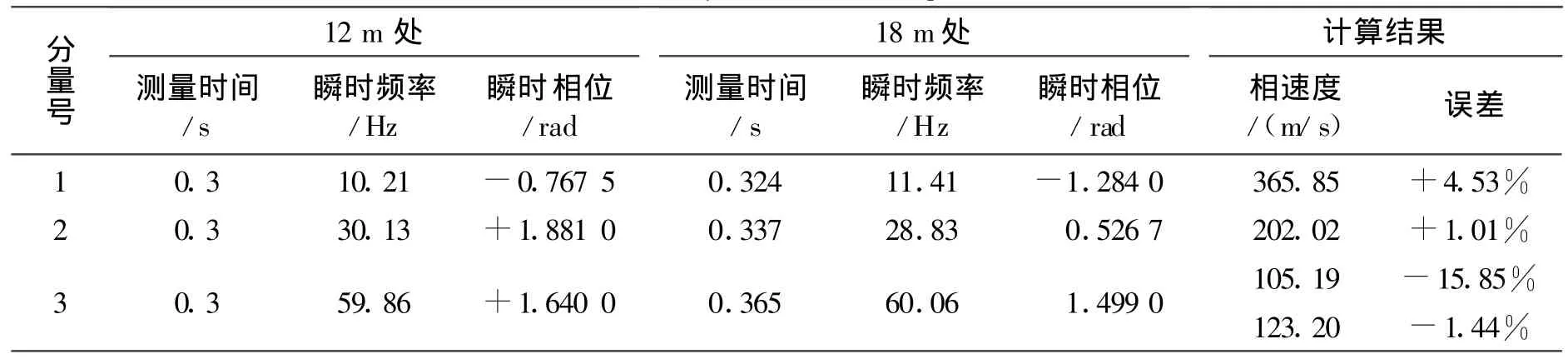
表6 校正相差计算相速度Table 6 Phase velocity with emendation phase difference

从表6中可以看出,低频、中频分量有效地避免了相位解缠。但高频分量周期太小,且群速度计算结果误差较大(见表3),故而实测相差与真实相差出现偏差。此时,实测相差需补上一个周期2π才能获得真实相差。

4 结 论

运用希尔伯特黄变换可以获得信号的时频-相位的精确分布信息,而异步相差和校正相差可以有效避免相位解缠,将上述方法用于进行信号的频散分析,不仅算法简单而且结果准确。但该方法部分细节依然有待改进:

(1)因为精度有限,不同时刻的相差不一定完全一致;而且瞬时频率在真实频率附近起伏,故不同时刻求取的相速度值会略有区别,所以确定某一分量的相速度时,可以对多个时间点的相速度进行平均处理;

(2)如果某信号含有的单分量信号数目较多,直接采用EMD可能效果不会很理想,此时可以采用经验模态频率分解[9,10](EMFD)的方法来获得IMF,即首先对原信号进行分频段窄带滤波,然后对每段滤波结果再单独进行希尔伯特黄变换。

[1] Dong-Soo Kim,Hyung-Choon Park.Determination of dispersive phase velocities for SASW method using harmonic wavelet transform[J].Soil Dynamics and Earthquake Engineering,2002,22(8):675-684.

[2] Jianghai Xia,Richard D Miller,Choon B Park,et al.Comparing shear-wave velocity profiles from MASW with borehole measurements in unconsolidated sediments[J].Journal of Environmental and Engineering Geophysics,2000,5(3):1-13.

[3] 科恩.时频分析:理论与应用[M].白居宪,译.西安:西安交通大学出版社,1998.LeonCohen.Time-Frequency Analysis:Theory and Applications[M].Translated by BAI Ju-xian.Xi′an:Xi′an Jiaotong University Press,1998.(in Chinese)

[4] Norden E Huang,Zhaohua Wu.A Review on Hilbert-Huang Transform:Method an Its Applications to Geophysical Studies[J].Reviews of Geophysics,2008,46(2):1-23.

[5] Norden E Huang,Zheng Shen,Steven R Long.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A:Mathematical Physical and Engineering Sciences,1998,454(1971):903-995.

[6] Norden Huang,Zhengshen,Steven R Long.A new view of nonlinear water waves:The Hilbert Spectrum[J].Annual Review of Fluid Mechanics,1999,31(1):417-457.

[7] Chau-Huei Chen,Cheng-Pling Li,Ta-Liang Teng.Surface-Wave Dispersion Measurements Using Hilbert-Huang Transform[J].Terrestrial,Atmospheric and OceanSciences,2002,13(2):171-184.

[8] 李白基,师洁珊,宋子安,等.地震面波的数字计算[J].地球物理学报,1977,20(4):283-298.LI Bai-ji,SHI Jie-shan,SONG Zi-an,et al.Digital Processing for Seismic Surface Wave Dispersion[J].Acta Geophysica Sinica,1977,20(4):283-298.(in Chinese)

[9] LI Jiang,XU Yixian.Analysis of dispersion of phase velocities using empirical mode frequency decomposition on SASW[C]//Proceedings of Near-Surface Geophysics and Geohazards.Chengdu:Science Press,2010:225-231.

[10] 程乾生,武连文.时间序列的经验模态频率分解EMFD[J].数学的实践与认识,2005,36(5):151-153.CHENG Qian-sheng,WU Lian-wen.The Empirical Mode Frequency Decomposition for Time Series Analysis[J].Mathematics in Practice and Theory,2005,36(5):151-153.(in Chinese)