频偏稳健的分级调制分类算法

冯 祥,梁伟洋

(空军第一航空学院,河南 信阳 464000)

1 引 言

信号调制制式的自动分类是软件无线电、认知无线电的重要技术基础[1,2],由于其在军事和民用通信系统中的广泛应用前景,调制分类的研究一直引起人们的极大兴趣。目前研究这一问题的方法可归纳为两类[3],即似然函数法和模式识别法。基于判决理论的似然函数法在加性高斯白噪声环境下,将调制识别的问题看成复合假设检验的问题,利用最大似然估计来达到识别的目的[4]。模式识别的方法一般分为3个步骤[3]:样本的获取和预处理,特征分析及提取,模式匹配和结果判决。文献[2,5-7]通过提取样本的高阶累积量、高阶循环累积量识别特征实现对PSK、QAM等调制类型的分类,取得了较好的试验结果。但这些文献没有考虑频偏等因素的影响。本文在Rayleigh衰落信道下,研究了存在频偏时ASK、PSK、SQAM等调制类型的分类问题。

2 信号模型及算法描述

考虑频偏的情况下,观测样本可以表示为

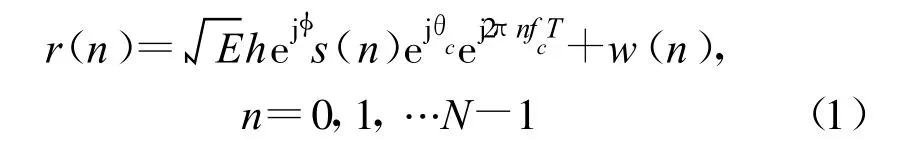
在存在载波频偏的情况下,由于频偏引起的相位旋转将使观测样本的星座图失去调制类型信息,随着观测样本的增加,样本的星座点将充满单位圆,此时直接从观测样本中提取分类特征将不能有效识别其调制类型。将式(1)进行如下变换:

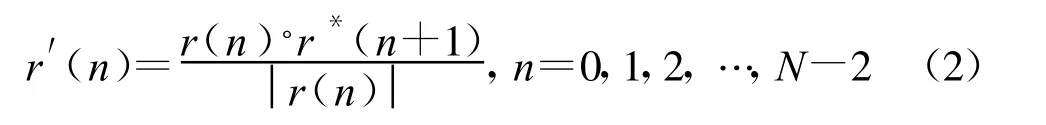
先不考虑噪声的影响,可以得到:

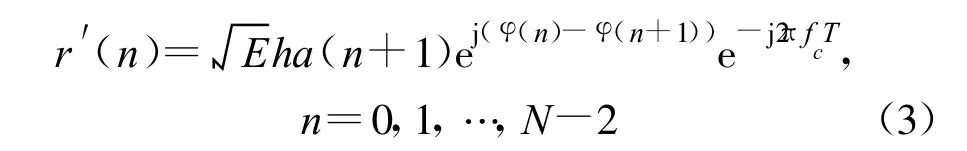
表1 衰落信道下备择分类集合的累积量Table 1 The cumulants of the candidate for modulation types under fading channel

为了对子集合{2SQAM,4ASK,8ASK}进行分类,定义反映样本幅度信息的分类特征σa:

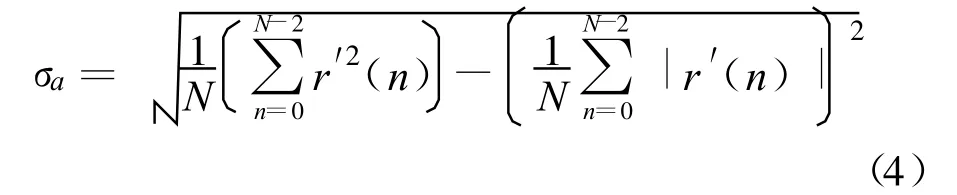
由于2SQAM星座的绝对值相等、符号相反,所以它不具有绝对幅度信息(σa=0);而4ASK和8ASK具有绝对幅度信息,为了进一步区分4ASK和8ASK,对样本作绝对值、中心化、归一处理后,4ASK对应的星座变为2ASK,仍然采用分类特征 σa进行分类。图1显示了算法的具体实现。

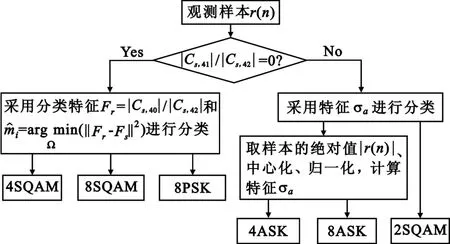
图1 基于四阶累积量分层调制分类算法Fig.1 Hierarchical modulation classification algorithm based on 4-order cumulants

3 性能仿真

为了验证图1描述算法性能,我们对算法进行了仿真试验。信道采用 Jakes模型,载波频率为900MHz,移动台的移动速度为10 m/s,码元速率为300 ksymbol/s,归一化多普勒频率为1×10-4。图2给出了在归一化频偏 fcT=0.1时信号调制方式的正确识别率随信噪比变化曲线。从图中我们可以看出,在低信噪比时,算法存在门限效应。在观测样本为500、信噪比约为8.4dB时,正确识别率达到0.9;信噪比大于14dB时,算法的正确识别率接近1。为了对比,图中还给出了Rayleigh信道下无频偏时的性能曲线,可以看出由于频偏的存在造成约3.6dB的信噪比损失。

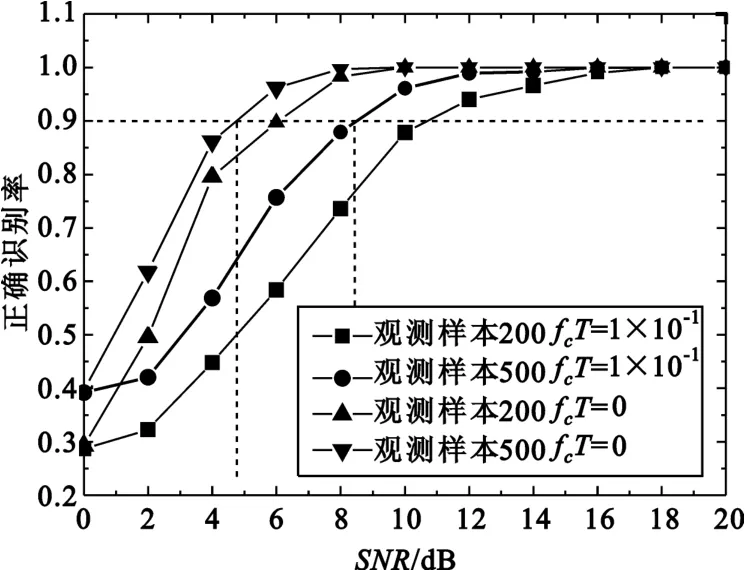
图2 分级分类算法性能(Rayleigh信道)Fig.2 The performance of the hierarchical classification algorithm under Rayleigh fading channel

图3给出了Rayleigh信道下,归一化载波频率偏差对分类算法的性能的影响,信噪比为14dB。在归一化频偏fcT≤0.1时,算法的性能变化较小;当fcT≤0.2时,算法的正确识别率大于0.9;随着归一化频偏fcT的进一步增加,分层算法性能显著下降,并且观测样本越多,对频偏越敏感。这是由于观测样本数量越多,使我们假设的帧不变衰落信道的条件只能近似满足,对分类算法的性能影响越大。

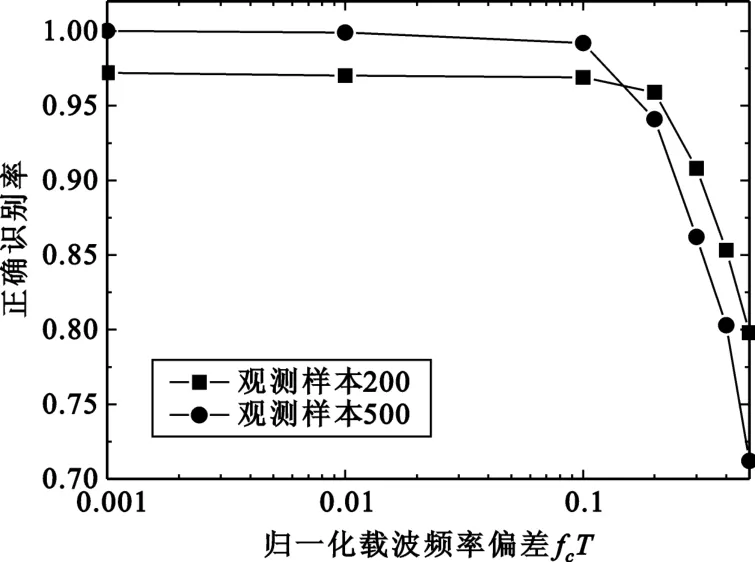
图3 载波频率偏差对分类算法性能的影响(SNR=14dB)Fig.3 The effect of frequency offsets on the performance of the classification algorithm(SNR=14dB)

4 结束语

本文在Rayleigh信道下,研究了频偏存在情况下的调制分类问题,通过对观测样本进行非线性变换,消除了由于频偏引起的相位旋转的影响。变换后观测样本的星座图与变换前相比较,仅仅旋转固定的相位-2πfcT,仍然保持原来对应调制方式星座图的形状。通过定义高阶累积量和幅度特征,提出了一种分层调制分类算法。仿真结果表明,在正确识别率为0.9时,与无频偏比较,算法有约3.6dB的信噪比损失。在归一化频偏小于0.2时,算法具有较好的性能。

[1] Kim K,Spooner C M,Akbar I,et al.Specific emitter identification for congnitive radio with application to IEEE 802.11[C]//Proceedings of 2008 IEEE Global Telecommunications Conference.New Orleans,LO:IEEE,2008:1-5.

[2] Zhang Q,Dobre O A,Rajan S,et al.On the second-order cyclostationarity for joint signal detection and classification in cognitive radio systems[C]//Proceedings of 2009 IEEE Canadian Conference on Electrical and Computer Engineering.St.John′s,NL:IEEE,2009:204-208.

[3] Dobre O A,Abdi A,Bar-Ness Y,et al.A survey of automatic modulation classification techniques:classical approaches and new trends[J].IET Communications,2007,1(4):137-156.

[4] Hameed F,Dobre O A,Popescu D C.Likelihood-based modulation classification:On the computational complexity and performance bounds[J].IEEE Transactions on Wireless Communications,2009,52(8):206-217.

[5] Swami A,Sadler BM.Hierarchical Digital Modulation Classification Using Cumulants[J].IEEE Transactions on Communications,2000,48(3):416-429.

[6] Punchihewa A,Dobre O A,RajanS,et al.Cyclostationarity-based algorithm for blind recognition of OFDM and single carrier linear digital modulations[C]//Proceedings of IEEE International Symposium on Personal,Indoor and Mobile Radio Communications.Athens,Greece:IEEE,2007:1-5.

[7] Spooner C M.On the utility of sixth-order cyclic cumulants for RF signal classification[C]//Proceedings of the 34th Asilomar Conference on Signals,Systems,and Computers.Pacific Grove,USA:IEEE,2001:890-897.

[8] 张贤达.现代信号处理[M].2版.北京:清华大学出版社,2002.ZHANG Xian-da.Modern Signal Processing[M].2nd ed.Beijing:Tsinghua University Press,2002.(in Chinese)