“电磁场”课程的散度和旋度研究型教学例析

黄 辉，张小青

（1.北京交通大学 电气工程学院，北京 100044；2.东南大学 毫米波国家重点实验室，江苏 南京 210096）

0 引言

“电磁场”课程是电气工程及其自动化专业以及电子信息工程、通信工程及电子科学技术类专业的一门重要的技术基础课程，为“电机学”和“电力系统”等课程奠定必要的理论基础。但是，由于“电磁场”课程的概念比较抽象，理论推导繁琐，对数学基础要求高，被学生认为是本科最难学的课程之一。

笔者根据多年的电磁场教学经验，发现学生对本课程的畏难情绪，直接来源于难以理解梯度、散度和旋度这几个基本概念。特别是散度和旋度两个概念，部分学生直到课程结束也没有正确理解。

目前，通常采用从宏观到微观的教学方法，即由通量引出散度，再由环量引出旋度。这种方法建立的模型易于表述，有关通量、散度的内容较易理解；但是，对于环量和旋度，同样的教学方法却具有一定的局限性。这是因为作为宏观量的环量本身就比较抽象，进一步描述微观的旋度作为有方向的矢量就更不易被学生接受。学生往往不理解为什么旋度有方向，对其方向代表的物理意义理解起来更加模糊。

笔者依据研究型教育理论，重新设计了关于散度和旋度的研究型教学模式。本文介绍了这种教学模式主要环节的设计，包括如何引出散度和旋度、如何阐述其物理意义、计算方法等内容。

1 教学环节的设计

1）引入问题

课程的一开始，笔者从科幻小说中的哈利波特与他神奇的隐身衣说起，引用“Controlling electromagnetic fields”［1］，阐述作者Pendry对控制电磁场从而实现隐身衣的理论设想。进述时，一边向学生展示电磁波在特定介质中发生弯曲且平滑绕过特定区域的动态视频，一边解释Pendry做出此大胆预测的理论基础仅仅是数学上的坐标变换原理和本课程的核心内容——麦克斯韦方程组。然后，从麦克斯韦方程组的微分形式自然地引出本次教学的重点：矢量场散度和旋度的计算及其物理意义。

这种以设趣与展演来激发学生学习兴趣的方式，是研究型教学模式的五个基本环节之一，是引导学生善学、乐学和会学的前提［2］。一方面，利用科幻小说中的神奇隐身衣吸引学生的注意力；另一方面，展示当前电磁研究的一个新领域及其标志性成果，把学生引领到科技最前沿，用科技进步的魅力提高他们对电磁场基础理论的学习兴趣，进一步可以转化为投身电磁场理论研究的兴趣。这样，学生对电磁场的学习就有了一个良好的开端。

2）散度的定义—从通量到散度

为了将抽象的通量概念形象化，在讲解过程中，笔者利用打气筒和气球做演示。打气筒向气球充气，模拟矢量进入闭合面S；反之，用气球放气模拟矢量流出闭合面S。借助这组实物，在充气和放气的简单动作中，结合通量的数学表达式，学生就能对通量的定义有比较感性的认识，进而比较容易理解通量的正负与闭合面内部的正负源的对应关系。最终让学生理解：引入通量这一概念的目的，就是为了衡量一个闭合面内部是否存在矢量的源。

当学生建立通量的概念之后，再用提问的方式引导学生进一步思考：借助通量只能判断整个闭合面内是否有源，能否更精确地描述源的确切位置？如何描述源的强度？

要回答上述问题，可以很自然地引出通量体密度——散度：压缩闭合面，到极限便成为点，再以这个已经成为点的小闭合面的通量除以它相应的体积，这就是散度。散度作为定义到空间点的微观物理量，可以准确定位源点，也能衡量该点源的强弱。

为了让学生对散度有更感性的理解，笔者引入了生活中常见的礼花作为形象化范例：如果把某一时刻喷出的礼花当作一根根矢量线，那么礼花筒所在的位置散度就大于0，是矢量的源；而且该点散度的大小与喷出礼花的疏密有关。

采用这种层层推进和兼以比喻的方式，学生能很好地理解从宏观通量到微观散度的推进过程。随后，学生也就能很自然地对奥氏公式加以理解和接受：既然散度是通量的体密度，那么其逆运算——对散度作体积分，就得到通量，即奥氏公式：

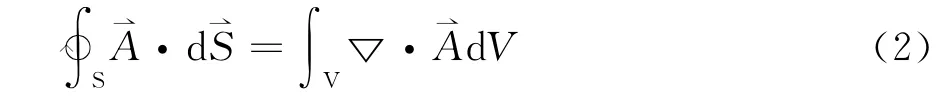
对于奥氏公式的讲授，可以采取这样的方式：在课堂上不作过多的数学推导，而偏重于剖析其物理意义——以散度这一概念作为桥梁，能够把一个矢量的闭合面积分转化为该矢量在空间中每一点的散度的体积分，从而实现了“面—点—体”的转化。

纵观从通量到散度的讲解，遵循了两个原则：一是突出重点，二是循序渐进。首先，讲解中注重突出通量与散度的物理意义，对高等数学已经涉及的数学运算仅仅给出要点帮助学生自我复习，而不作过多阐述。这种指要与自学也是研究型教学的基本环节之一，是可以帮助学生自主、自为和探究的关键环节［2］。此外，整个讲授内容，从宏观量的通量到微观量的散度，以及利用散度完成的从“面—点—体”的转化过程。我们始终采用层层推进的方式，注重其内在的逻辑性，引导学生自行理解从而掌握。对此内容的精讲，既训练学生的逻辑思维能力，也为后续的从环量引出旋度的讲授作铺垫。

3）旋度的定义—从环量到旋度

从环量引出旋度与从通量引出散度，二者思路有相似之处，但更有不同的地方。引导学生注意到它们的相似与不同之处，正是散度与旋度的研究型教学设计的要点。

这个讲授环节以一个设问开始：“既然以散度为桥梁，可以把一个矢量的闭合面积分转化为相应的体积分，那么，能否对应的，定义另一个物理量，把矢量的闭合线积分转化为面积分呢？”

笔者把这个设想在黑板上写成：“线—点—面”，加上显著的问号。随后，始终围绕这个设想进行旋度的讲解。先定义闭合线积分对应的物理量—环量。对一条闭合路径L，矢量的环量为

环量表征了在选定的闭合路径上该矢量场是否有涡旋的趋势，可以描述此闭合路径内部是否有引起涡旋的源和涡旋趋势的大小。

笔者以形象化的图1所示的水车和流速场为例：以水车外周边为路径L，考虑水流流速矢量。如果流速均匀且平行（无涡旋），则沿路径L水流速度的环量为0，水车静止；如果水流发生涡旋，环量不为0，水车将转动；而且水车在不同位置转动的角速度也有所不同，表明同样的闭合路径L处于不同位置所对应的环量不同。

图1 环量物理意义的阐述

随后，比较环量与通量的共同点：通量和环量都是宏观量，环量只能表明在选定的闭合路径中是否有涡旋源，不能描述空间点的性质。然后，引导学生思考：可不可以也为涡旋源准确定位并且衡量涡旋源的强弱呢？就像从通量引出散度一样？

由于有了从通量引出散度奠定的基础，学生很自然地会仿照其将“面”压缩成为“点”的思路，设想将线积分中的“线”也压缩成为“点”。这个设想一经提出，笔者就引导学生继续将设想深入实现。

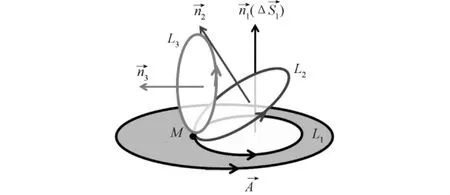
图2 旋度物理意义的阐述

借助多媒体分步演示的图2，笔者与学生共同研讨如何把“线”压缩到“点”。首先，给出流速场中一根流速线、一条闭合路径L1及其法线方向n1，以及将L1压缩而成的点M。然后提示学生：如果照搬从“面”压缩成为“点”的思路，即计算压缩到点M后的闭合路径L1所对应的环量再除以闭合路径所围成的面积，得到环量面密度，整个过程会不会有什么问题？当学生思考时，再给出另外两个同样也可以压缩到点M的闭合路径L2和L3作为提示，为学生进行如下引导。

（1）比较闭合路径L1、L2和L3对应的环量和环量面密度的大小。由于L3与矢量线垂直，所以环量为零，环量面密度也为零；而L1和L2对应的环量和环量面密度均不为零。表明：在同一位置点（如点M）的不同的闭合路径，法线方向不同，所对应的环量也不相同，从而同一位置点的环量面密度并不唯一。说明无法直接套用散度的定义方式得到新物理量，应予以修正；

（2）确定闭合路径L1、L2和L3对应的环量和环量面密度的关系。容易发现：L1对应的环量及其面密度最大，而且其他路径（如L2和L3）对应的环量，都可由L1对应的环量值乘以L1与所求路径夹角的余弦值求得。

（3）讨论特殊路径L1。首先，它是使该点环量及其面密度取得最大值的闭合路径；其次，其他任意路径所对应的环量均可由它间接求得；另外，它的法线正好是引发矢量涡旋的轴线。

最后，建立在这一特殊路径上，定义了旋度：大小是把这条特殊的“线”压缩到“点”而得到的环量面密度，即该点环量面密度的最大值；方向是该特殊路径的法线方向，即环量面密度取最大值的曲面方向。通俗一点是：某点旋度的方向就是该点涡旋源的轴线方向，而旋度的大小表征了场量绕着这一点涡旋趋势的大小。

根据旋度的定义，可以得到斯托克斯公式：对旋度作面积分，得到环量。

最后，通过对旋度的定义，证实了最初的设想：把一个闭合线积分通过对每一点求其旋度，转化为一个面积分。

2 研究型教学理念的深化

关于旋度定义的教学设计，遵循的主线为，仿照从通量到散度（“面—点—体”）的思路，实现“线—点—面”，由环量得到旋度。整个教学活动，重视问题解决的思维过程，在立足教材内容的同时，有意识地把静态知识展示成为动态的科学探究过程。

另外，研讨与回顾环节是夯实与深化知识的重要保障，也是研究性教学的重要环节之一。此环节应提炼所学到的知识、能力，引导学生反思和总结解决问题的思维过程，并揭示出隐含的科学方法和思维脉络。笔者注重学生在知识获取过程中的情感体验，从该教学过程中提炼出如下人文精神，以培养学生积极探索未知世界的科学态度，如下的体会值得强调。

1）成功并非偶然

课堂讲授中，从有设想开始，到最终得到验证，只用短短十几分钟。但是在实际的科学研究中，这一探索过程可能很长。笔者引入一则故事：法拉第从“既然电能生磁，磁是否能生电”的疑问开始，到实现这一设想花了整整9年。一次次失败面前，他并没有气馁，而是不断调整，直到最终的成功。

这则故事很自然地向学生们传递一个信息：成功通常要经历漫长的痛苦，只有不轻言放弃的人才有可能成功。如此自然地将人文精神融入到专业教学中去，可以达到提高学生承受挫折和失败的能力，从而达到最终提高情商目的［3］。

2）大胆设想，小心验证

科学的进步和知识的增长永远始于问题，必须先有大胆的设想，再加以科学的探索。这里值得借鉴的有两种探索方法：一是“同”中寻“异”，“异”中求“同”。同样是压缩，压缩面和压缩线就不同，从而引出了不同的物理概念；二是数学与物理结合，把生动的物理学概念同数学结合起来，再充分利用数学这一工具，来推进物理的不断发展。法拉第在实现了“磁生电”的夙愿以后，麦克斯韦把其物理思想作了数学上的综合和引伸，定义了新的物理量—位移电流，继而得到了涵义深远的麦克斯韦方程组。

这样，一方面向学生介绍了电磁发展史，另一方面也帮助学生消除对电磁场课程的神秘感，激发他们学习“电磁场”课程的积极性和主动性；同时可以了解科学家的科学研究方法，培养他们的科研兴趣。

3 结语

笔者通过对“电磁场”课程几年的教学体会，作了一次关于散度与旋度的研究型教学模式的设计和实践，取得了很好的教学效果。本文获得北京市第六届青年教师基本功大赛理工组A组的一等奖和最佳演示奖；作者之一的张小青老师获最佳指导奖。

［1］Pendry.Controlling eleclromagnotic field［J］.sceince，2006.6

［2］吴明赞.“工程电磁场”中静电场的研究型教学实践［J］.南京：电气电子教学学报，2009，31（6）：104－105

［3］龚杰星.在电类基础课教学中进行情商教育［J］.南京：电气电子教学学报，2009，31（4）：6－7