正弦交流电教学中的解题技巧
徐志跃
(北京航空航天大学 电工电子中心,北京 100191)
0 引言
对于工科学生来说,在学习“电路分析”、“电工学”和“电工电子技术”这一类专业基础课时,必须做够一定数量的习题,才能对教师讲述的内容进行消化和掌握[1]。然而在学习正弦交流电的内容时,除了有原来较为熟悉的电阻元件R之外,还有储能元件、电容器C和电感器L。电阻元件R上的电压和电流成比例关系,电容器C和电感器L上的电压和电流为导数或积分的关系。由RLC组成的正弦交流电路,不论是串联、并联还是混联,各元件之间的电压和电流不再是简单的加减关系,由于相位差形成了三角形的关系[2]。学生有时简单地把交流电路当作直流电路来处理,导致使解题结果发生错误[3]。
我们可以利用相量图描绘出各个电压、电流之间的大小和相位关系。从相量图的几何关系上找到解决问题的突破口,可以起到事半功倍的效果[4]。下面我们对正弦交流电路中的几个典型例题加以分析,希望能够帮助学生克服学习交流电的困难,找到一些交流电路解题规律和技巧,建立学习的自信心。
1 电容补偿
[例1]RLC并联电路如图1(a)所示。已知开关K闭合前后电流表A的读数不变,试求电容器的容抗XC与电感器的感抗XL之间的关系,其解法如下。
(1)开关K断开时的相量图如图1(b)中实线所示。以输入电压U为参考相量,电阻里的电流IR与电压U同相;电感里的电流IL滞后于电压U90°。电路的总电流滞后于输入电压,电路为感性的。电流表的读数为电路的总电流

图1 阻抗测量
(2)开关K闭合时的相量图如图1(b)中虚线所示[5]。为了使开关K闭合前后电流表的读数不变,即OA=OB,此时电路必为容性的,并且IC=2IL,即XC=XL/2。
2 电感线圈参数测量
[例2]电感线圈参数(直流电阻r和电感量L)的测量电路如图2(a)所示。将被测电感(r,L)与一个已知的电阻R串联后接到交流电压U,用交流电压表分别测量U1、U2及U 的值,试计算参数r和L[6],其解法如下。
以电流I为参考相量,电阻R上的电压与I同相。被测电感线圈上的电压可以分解为与I同相的电阻r上的电压Ur和与I垂直的纯电感上的电压UL,如图2(b)所示。(虽然它们并不存在,但可以这样去想象)[7]。
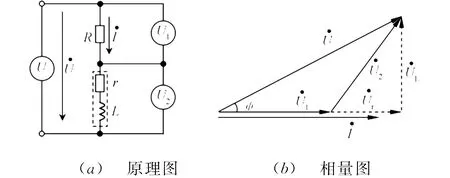
图2 参数测量
由余弦定理可知

则纯电感电压UL=Usinφ
线圈电阻电压Ur=Ucosφ-U1
电路中电流I=U1/R
则线圈电阻r=Ur/I
线圈的电感L=UL/(ωI)
3 利用谐振解题
[例3]电路发生谐振如图3(a)所示。已知电压U,及I1=I2,且电流I与电压U同相,试求电路参数R、XL和XC。其解法如下。
因为电路中电流I与电压U同相,所以电路发生谐振,即整个电路的复阻抗的虚部为零,由此可以得到R、XL和XC的一些关系式。这时求解较为复杂的方程式,容易出错。我们可以利用相量图地描绘出电路中各个电压和电流之间的相位关系,如图3(b)所示[8]。

图3 电路谐振状态
现以电容器C上的电压U2为参考相量,则电阻R里的电流I1与U2同相,电容器C里的电流I2超前于U2为90°,总电流I =,且超前于U2为45°。电感上的电压UL超前于其电流I为90°,即UL超前于U2为135°。最后,由于电压U与电流I同相,所以电压U与电流I平行,并与UL相交。显然,电压U、UL和U2构成了等腰直角三角形,即U=UL=U2/。由此很容易计算出电路参数R、XL和XC:

4 复阻抗的测量
[例4]测量复阻抗Z的电路如图4(a)所示。将可变电阻器R接到交流电压上,将被测复阻抗Z与已知的电阻R1串联后接到同一交流电压上。改变滑动端C的位置,电压表V的读数随之改变。当C滑动到某一位置时电压表V的读数达到最小值,试计算复阻抗Z值[8]。其解法如下。
(1)一般解法
以Uab作为参考相量,假设复阻抗Z为容性的,即电流I1超前于电压Udb,阻抗角为φ3,画出电路的相量图如图4(b)实线所示。

图4 阻抗测量
根据题意,当滑动端c达到某一特定位置时,电压表V的读数达到最小值,即电压Ucd达到最小,并且线段cd⊥ab。此时电压Ucb、Uac、Ucd均已知,可以计算出电压Udb、Uad。再由余弦定理得到φ1、φ2,从而得到复阻抗Z的阻抗角φ3。复阻抗Z的模为|Z|=Udb/I1= Udb/(Uad/R1)。
因此,复阻抗Z=|Z|∠φ3
(2)最简解法
相量图如图4(b)实线所示,仍然假设复阻抗Z为容性的。注意到电阻R1上的电压Uad可以从两方面得到。
一方面,从原理图上看,Uad是R1,与Z串联后对输入电压U 分压的结果。即ad= (Z)/(R1+Z)。另一方面,从相量图上看,ad=ac+cd=Uac+j Ucd。
不难求得复阻抗Z= (Uac+j Ucd)R1/(Ucb-j Ucd)
(3)综合分析
以上分析是假设复阻抗Z为容性,如果Z为感性,则其中的电流I1滞后于电压Udb,得到的相量图如图4(b)虚线所示。显然,它与实线的情形是完全对称的。综合以上两种情形,有(Z)/(R1+Z)=Uac±j Ucd。因此,Z= (Uac±j Ucd)R1/(Ucb-j Ucd)。
5 功率因数的提高
正弦交流电路中,有功功率p取决于电压U、电流I以及U、I之间的夹角的余弦cosφ(功率因数)的乘积。提高电路的功率因数,可以充分提高电源的潜力,降低电网传输线的功率损耗,具有重要的意义[9]。功率因数低下的主要原因是感性负载使用过多,如工厂里的电动机,日常生活中的日光灯、节能灯等。要想提高功率因数可以并联电容进行补偿,如图5(a)所示。补偿的原理如图5(b)所示。

图5 提高功率因数
并联电容C之前,线路上的电流I等于电感里的电流I1。尽管电流I1很大,但由于U与I1的相位差φ1很大,cosφ1很低,即I1的有功分量IP很小。并联电容C之后,由于电容里的电流IC超前于电压U为90°,线路上的电流I等于电感电流I1与电容电流IC的相量和。I比I1小得多,但是两者的有功分量却是相同的。此时总电流I与电压U之间的夹角φ比之前的φ1减小,功率因数cosφ大为提高。从这个意义上讲,并联电容C提高功率因数的实质就是保持有功分量不变的前提下,降低线路上的总电流。
从图5(b)不难看出,此时电路里的电流I落后于电压U,电路仍然是感性的。这种情况称为欠补偿。当IC与电压U相交时,电流I与电压U同相位,cosφ=1.0,称为完全补偿。当IC超过电压U时,电路变为容性的,称为过补偿。
如果要求将电路的功能因数从cosφ1提高到cosφ,补偿电容C的值如何计算呢?
从电路图上看IC=UωC
从相量图上看IC=I1sinφ1-Isinφ
因为有功功率P=UI1cosφ1=UIcosφ
因此I1=P/(Ucosφ1);I=P/(Ucosφ)
所以IC=P/U(tanφ1-tanφ)
电容器C的值C =P/[U2ω(tanφ1-tanφ)]
[1] 秦增煌.电工学(第六版)[M].北京:高等教育出版社,2004
[2] 邱关源.电路(第五版)[M].北京:高等教育出版社,2006
[3] 上官左黎.“电路分析基础”课程改革的思考[J].北京:北京邮电大学学报,2000.3,2(1):44-46
[4] 周茜,徐亚宁.《电路分析基础》课程教学设计的创新与实践[J].桂林:桂林电子工业学院学报.2004.8,24(4):113-116
[5] 唐介.电工学(少学时)学习辅导与习题全解(第二版)[M].北京:高等教育出版社,2005
[6] 孙玉坤,陈晓平.电路原理[M].北京:机械工业出版社,2006
[7] 陈晓平,付海军.电路原理学习指导与习题全解[M].北京:机械工业出版社,2007
[8] 刘崇新,罗先觉.电路(第五版)学习指导与习题分析[M].北京:高等教育出版社,2006
[9] 唐介.电工学(少学时)[M].北京:高等教育出版社,2005

