基于图像平滑度的WBCT算法研究与改进
周临川,赵 辉,王 帅
(山东大学 信息科学与工程学院,山东 济南 250100)
0 引言
随着计算机网络的发展,通过计算机网络来浏览和传输视频图像越来越普遍,随之而来的是对传输图像的质量要求也越来越高,如何能够在给定的带宽下提高图像的传输质量,成为人们越来越关注的问题,各种图像压缩算法成为研究的热点。离散小波变换DWT(Discrete Wevelet Transform)是多尺度图像分析工具的一种,它克服了传统离散余弦变换DCT的块效应缺点,且图像压缩效果良好。但是DWT只能够检测有限的方向信息,即水平、垂直和对角,不能够顺利捕获二维图像中的线和面奇异,不能很好地存储图像的轮廓和纹理信息。为了解决DWT存在的方向性问题,许多新提出的变换中都包含了多分辨率分析,其中文献[1]提出了Contourlet变换。这种变换允许在不同的方向上进行不同程度的临界采样,来捕捉代表方向性的高频成分,以便有效表示图像的轮廓和纹理。但是,由于Contourlet变换采用的LP(Laplacian Pyramid)分解是一个冗余分解,因此不适于图像的压缩。为了消除冗余,文献[2]在Contourlet变换的基础上提出了基于小波的Contourlet变换WBCT。WBCT能够更好地保存图像的重要特征,如边缘和纹理等。
小波理论的成功应用为图像编码提供了更多的灵活性,其中最具有代表性的是嵌入零树小波编码算法EZW[3]和在此基础上提出的多级树集合分裂编码算法SPIHT[4]。该算法不仅具有出色的率失真性能,而且是完全嵌入式的,可以实现渐进式编码,因此成为小波嵌入式编码的通用基准,也是目前最有效的小波图像编码算法之一。
WBCT对于有大量纹理的图像压缩效果明显,但对于较平滑的图像,其恢复图像效果要低于一般的小波编码图像。因此,本文在边缘检测的基础上采用改进的基于图像平滑度对图像进行小波变换和Contourlet变换,使之能够更好地保存图像中的有效信息。
1 WBCT变换
WBCT采用小波变换取代LP滤波器实现多分辨率分解,避免了LP滤波器引入的数据冗余,然后将小波分解得到的高频子带进行方向滤波器分解。由于小波分解和方向滤波器组分解都是无冗余的且都是完全重构的,因此整个过程不会产生数据的冗余,形成了两级非冗余完全重构的滤波器组,能够有效地逼近包含轮廓和震荡模式的图像。
1.1 图像平滑度
图像的纹理信息对于人类的视觉系统和数字图像处理技术都具有非常重要的意义。它是图像的基本特征之一。本文对图像中的像素和其邻域像素均值之差统计分布。图像在 (i,j)位置的灰度值为I(i,j),对图像中的任意像素,定义以当前图像为中心,3×3范围内的像素为当前像素的邻域S。定义当前像素与其邻域像素的差值:

考察随机变量X的概率分布,其概率密度函数为f(x)。图1为Lena标准图像和其随机变量X的概率分布曲线。
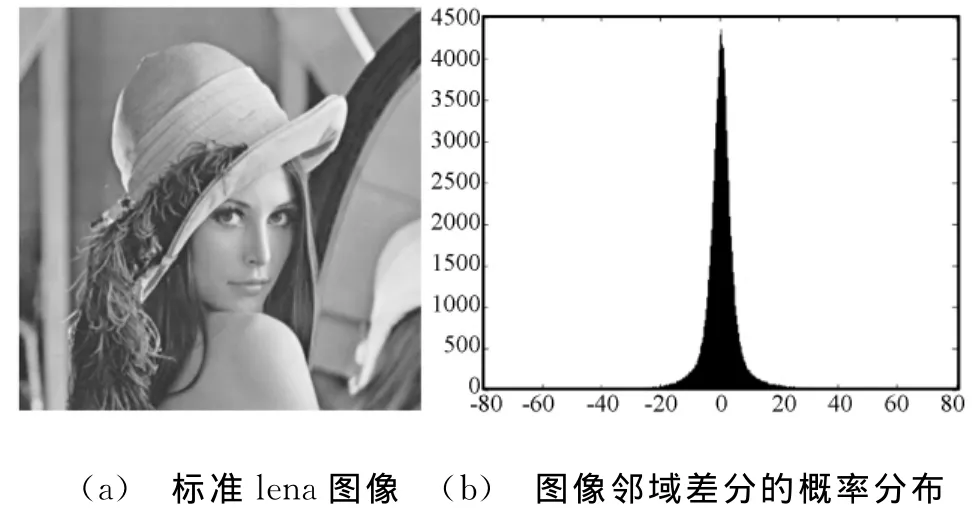
图1 Lena图像及其邻域差分的概率分布
随机变量X的方差反映了当前像素偏离邻域像素均值的剧烈程度,可以作为图像平滑度的标准,因此定义图像平滑度为

P取值越大,则图像平滑性越差。根据图像平滑度不同,本文将图像分为五类:P40,40<P80,80<P120,120<P160,P>160。
1.2 改进算法
同WBCT变换一样,本文的改进算法分为两个滤波器阶段。第一阶段为小波分解,采用具有线性相位、对信号压缩效果更好的CDF9-7小波五层分解,比经典Mallat算法的运算量减少20%到50%。第二个阶段是方向滤波,本算法根据图像平滑度的大小对图像进行不同程度的方向滤波。当P40时,本算法认为该图像比较平滑,只对最高频的子带进行角分解;当40<P80时,对该图像的最高频和次高频子带进行角分解;…;当P>160,本算法认为该图像纹理细节丰富,对所有高频子带均进行角分解。对参与角分解的最低频子带进行四方向角分解,随着子带频率增大,角分解方向加倍。图2为WBCT的三层分解示意图。
在改进WBCT与SPIHT算法相结合的过程中,针对改进WBCT变换后的小波系数的特点,采用不同于传统小波系数空间方向树结构。

图2 WBCT的三层分解示意图
在小波系数空间方向树结构中,我们通过不同子带小波系数之间的依赖关系来定义小波系数的亲子关系。在改进WBCT变换中存在三种小波系数之间的亲子关系,这三种关系取决于父带和子带是否参与角分解而定:①如果父带和子带均没有参与角分解,小波系数间的亲子关系与一般小波相同;②如果父带没有参与角分解,而子带参与角分解,则子带方向性数目为父带4倍,其亲子关系如图3(a)所示;③如果父带和子带均参与角分解,子带系数所在的方向性数目是父带系数所在的方向性数目的2倍,那么4个子系数将存在于2个相邻方向的子带中,这2个方向子带是由父带方向分解而来的,如图3(b)所示。
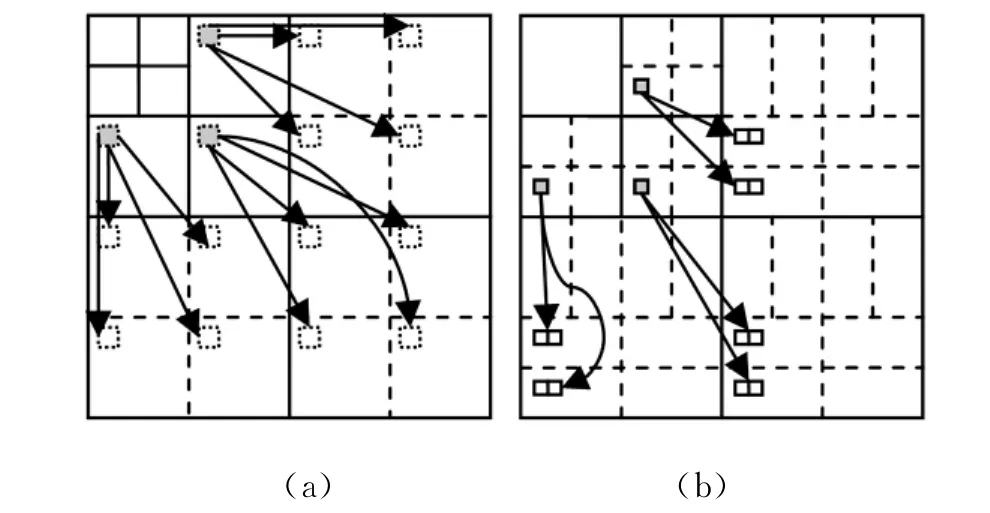
图3 改进WBCT变换空间树的两种亲子关系
2 改进SPIHT算法
SPIHT算法延用了EZW算法的零树结构,充分利用小波变换后图像能量的集中性和各层小波系数的多尺度结构,将根节点和子节点划分为一个集合,然后采用合适的集合分割排序,通过初始化、排序扫描、细化扫描和量化步长更新四个过程完成图像的嵌入式编码。SPIHT算法具有较高的信噪比和较好的图像恢复质量,实现了图像分层的渐进式压缩编码,是非常适合嵌入式图像的编码算法。但是,SPIHT算法本身也存在着不足:①原算法在排序过程中存在大量的重复扫描。每次变换阈值,对上次遗留的非重要元素还需要逐个与新阈值比较,增加了编码时间;②实验表明,最低频子带系数幅值要比其他子带系数高出很多,若进行零树编码则初始阈值较大,扫描次数多;③没有充分考虑人眼的视觉特性和小波变换系数的特点,对所有小波变换子带进行同样重要的编码。
针对本文算法中小波系数的特点和SPIHT本身存在的缺陷,本文对SPIHT算法做如下改进。
1)建立最大值表
本文算法中小波系数之间的亲自关系复杂,采用SPIHT算法,在每个新的阈值下判断D(i,j)和L(i,j)的重要性时都要把所有子孙节点系数与阈值比较,存在大量的重复查找子节点操作,D(i,j)是点(i,j)所有后代的座标集合,不包括(i,j)点本身。L(i,j)是点(i,j)除直接后代外,所有后代座标的集合。因此可以通过建立两个最大值表来改进,一个是D(I,j)最大值表,一个是L(i,j)最大值表。最大值表只需要原图像1/4大小。实验表明,即使比特率是0.1bpp,在扫描过程中,也扫描了最大值表中90%以上的节点。因此,在编码前通过逆向扫描方式建立L(i,j)最大值表,然后通过L(i,j)来建立D(i,j)最大值表,通过这种方法,可以最大程度上减少比较的次数。在以后的过程中,只将最大值表中的值与阈值比较即可,计算量大为减少。
2)单独处理最低频子带
把最低频子带与其他子带分开处理,对其采用无损Huffman编码,其他子带仍然采用SPIHT编码。这样第一次零树编码初始阈值为除最低频子带之外的系数最大值,扫描次数大为减少。
3)对小波系数进行加权
从客观角度,小波系数的大小表示了其重要程度;从主观角度,小波系数的重要性与人眼的视觉特性敏感度有关,人眼对某个频带越敏感,该频带的小波系数就越重要。基于人眼视觉特性的小波域系数量化方法,可以增强图像的主观效果。
实验证明,Mannos模型是目前应用比较广泛的一种视觉模型,其调制传递函数如式(3)所示。其非线性部分是幂函数,模拟了视觉的非线性特性,线性部分则反映了视觉的带通特性,这正好与小波变换的性质相一致。
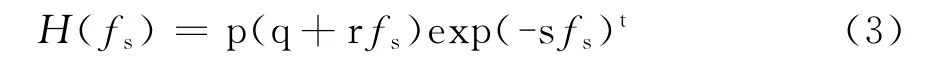
式中,fs=为空间频率,fx和fy分别是水平频率和垂直频率,fs、fx和fy单位均是周/度,s、p、q、r和t均为常数,根据经验来设定。本文采用一组性能较好的数据,取s=0.114,q=0.192,r=0.114,p=2.6,t=1.1,则传递函数为

3 测试结果
我们用本文方法对三幅512x512大小的灰度图像Lena、Barbara和Peppers用本文方法进行仿真,并与传统的小波变换、WBCT与SPIHT算法相结合的编码方法进行比较。三种编码方法均采用5层小波分解。
由表1我们可以看到,本文算法编码后Lena和Peppers图像的峰值信噪比PSNR高于WBCT和小波变换。对于纹理和轮廓信息比较丰富的图像如Barbara,本文算法PNSR略高于WBCT,远大于小波变换。对于比较平滑的图像如Lena情况则相反。另外,本文算法通过建立最大值表大大减少了比较的次数,编码时间减少1/4左右。实验证明,该方案在保护图像细节和纹理方面具有优势,并且缩短了编码时间,而且图像的主观质量明显提高。其重构图像如图4所示。
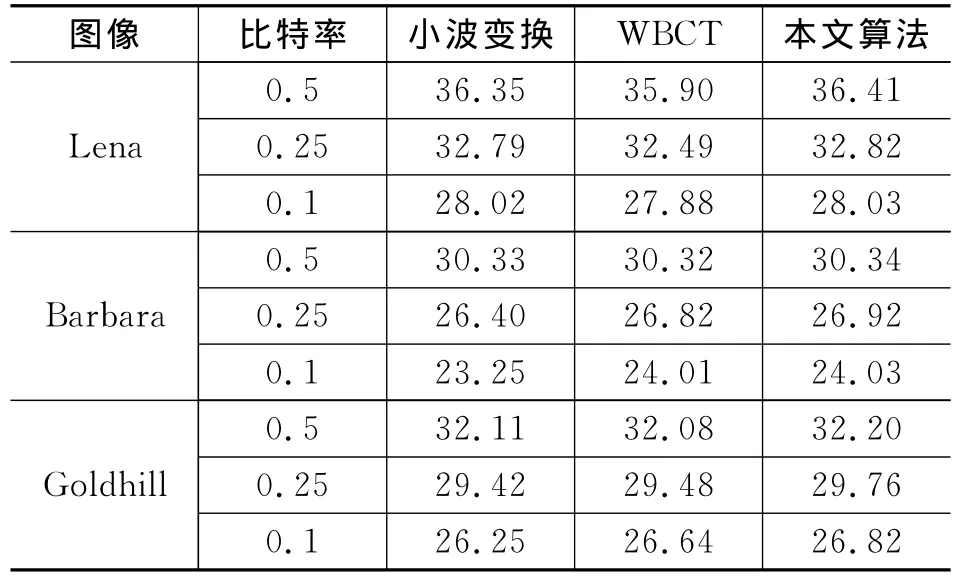
表1 不同比特率(bpp)下图像PNSR(dB)比较


图4 Barbara图像(0.25bpp)的重构图像
4 结语
基于小波的Contourlet变换WBCT的图像编码算法是近年来新兴的研究领域。WBCT采用小波变换来代替冗余的LP变换,用SPIHT算法中的空间方向树结构,实现了嵌入式编码器,能够更好地表示图像的纹理和轮廓信息。
本文通过对不同平滑度的图像进行分类,并对图像进行不同程度的方向滤波;对小波系数进行加权,使其更符合人眼的视觉效果;另外,对SPIHT算法做了一些改进。实验结果表明,本文所采用的方法优于原WBCT算法,对于不同平滑度的图像进行不同的处理,在任意比特率下都有良好的性能,对各个方向的边缘信息进行了更好的保存,并且能更好的符合人眼的视觉特性。
[1]Duncan D Y,Po M N.Do Directional multiscale modeling of images using the contourlet transform[J].IEEE Trans.on Image Processing,2006,15(6):1610-1620
[2]R Eslami,H Radha.Wavelet-based Contourlet Coding Using an SPIHT-like Algorithm[C].Princet-on:Conference on Information Sciences and Systems(CISS),2004
[3]Shap iro J.Embedded image coding using zero trees of wavelets coefficients[J].IEEE T ransactions on Signal Processing,1993,41(12):3445-3462
[4]Said A,Pearlman W.ANew,Fast and Efficient Image Codec Based on Set Partitioning in Hierarchic-al Trees[J].IEEE Trans on Circuits Systems for Video Technology,1996,6(3):243-250
[5]Canny J.A Computational Approach to Edge Detection[J].IEEE Trans on PAMI,1986,8(6):6792698

