基于小波能量熵的水下目标磁场信号去噪

方 石 陈朝宏 殷正保

（1.海军驻宜昌地区军事代表室, 宜昌 443003； 2.中船重工集团第710研究所, 武汉 443003）

1 引言

小波变换理论为噪声消除问题提供了一个新的思路。其主要思路是根据小波变换的线性，如果噪声能量明显小于信号能量，则与噪声对应的小波系数也将明显地小于与信号对应的小波系数；因此可通过将小于某一阈值的小波系数去除从而实现去噪。小波去噪中的关键问题是阈值的确定。目前主要有 MAD（Median absolute deviation）、MINIMAX（MINImaland MAXimal value）、SURE（Stein’s unbiased risk esti-mate[2]）和HYBRID（软硬阈值混合） 等方法[3]用于确定阈值。但这些方法在确定阈值时都带有一定的猜测性，因此去噪效果不稳定。

本文结合信息论中熵的理论，以及多尺度下小波熵的定义，在分析不同分解尺度上信号和噪声不同的能量分布特性基础上，通过对不同分解尺度上小波系数进行子带分解，计算不同子带分量的小波熵，利用最大小波熵自适应地选择阈值，实现水下目标磁场信号的有效去噪。

2 小波变换及小波熵

设x（t）是平方可积函数，即x（t）∈L2（R），则x（t）的小波变换为：

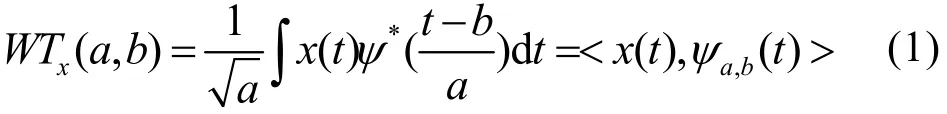
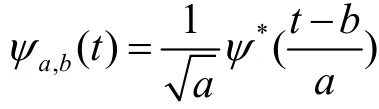
（1） 容许条件

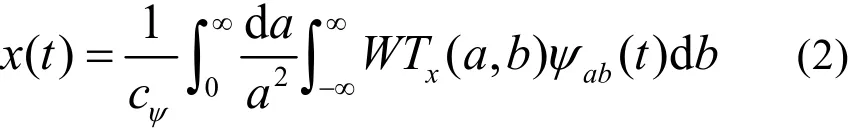
（2） 正规性条件

为使ψ（ω）在频域上有较好的局域性能，要求|WTx（a,b）|随a的减小而迅速减小，这就要求ψ（t）的前n阶原点矩为0，且n值越高越好。即

P=1～n，且n值越大越好

对于（1）式，如果对尺度参数和位移参数按幂级数作离散化，即令a=a0j，b=ka0j则小波函数变为：

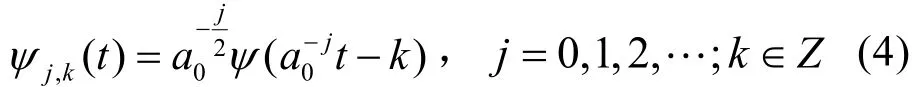
相应小波变换为

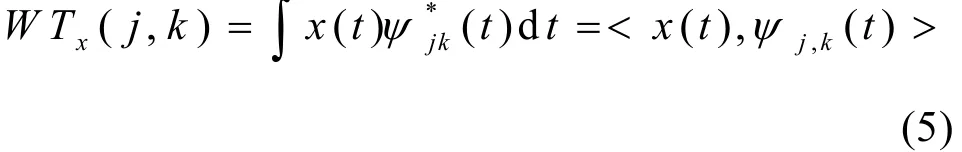
式（5）就是离散小波变换（DWT），其输出结果便是小波序列的系数djk，信号x（t）可用小波基函数和小波系数表示为

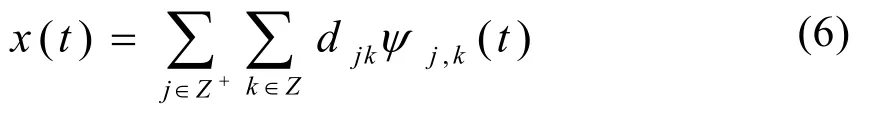
由小波标架理论可知，当小波基函数是一组正交基函数时，小波变换具有能量守恒性质，即

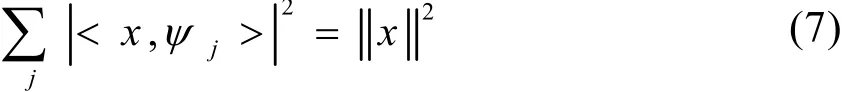
此时，单一尺度下小波系数的平方和就定义为该尺度下的小波能量[5]。

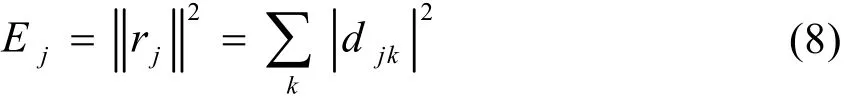
信号总能量就为各尺度下小波能量之和

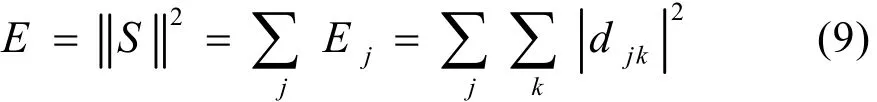
这样，相对小波能量可定义为

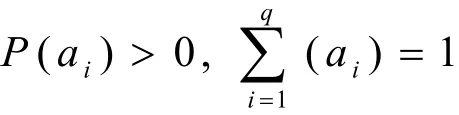
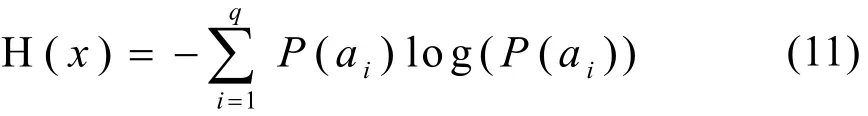
因此，信号熵值的大小实际上反映了其概率分布的均匀性，即信号的概率分布越接近无序的分布，其熵值也就越大；反之其熵值就越小。如果把小波变换的系数矩阵处理成一个概率分布序列，则由它计算得到的熵值就反映了这个系数矩阵的稀疏程度，也就是信号概率分布的有序程度，这种熵就称作小波熵。如果将（11）式中的P（ai）换成（10）式中反映某一段信号能量强度比例的相对小波能量pj，则小波熵可定义为：

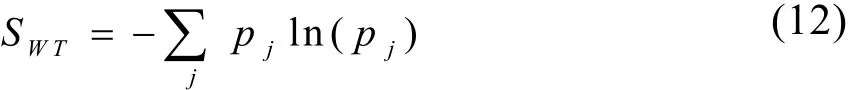
3 基于小波熵的阈值确定法

对于加性噪声模型，经过正交小波变换后，能最大程度地去除有用信号的相关性，将能量集中在少数稀疏的、幅度相对较大的小波系数上。而噪声对应的小波系数仍然互不相关，并将分布在各个尺度下的所有时间轴上，且幅度不是很大。如果在小波变换的各个尺度下保留那些集中了有用信号大部分能量的少数小波系数，而将其他点置零，或最大程度地减小，再利用处理后的小波系数做小波逆变换，就可实现对噪声的抑制。因此，小波阈值在去噪过程中起到了决定性的作用，将直接影响到小波去噪的效果。

令观察信号为

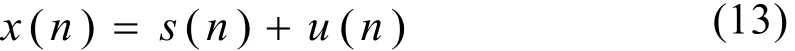
式中，s（n）为有用信号；u（n）是噪声。记xλ是对小波系数施加阈值λ后重建的信号，uλ是xλ中残留的噪声，即uλ=xλ-s。由xλ近似s所产生的“风险函数”定义为

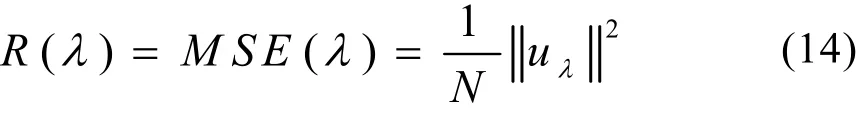
式中，MSE是均方误差，N是数据长度。

文献[6]和[7]证明了如果λMSE使E{R（λ）}为最小，则

式中，符号～表示渐进等效，λMSE称为基于均方误差的最小风险阈值。由于实际工作中最小均方误差很难估计，因此，通常使用通用阈值

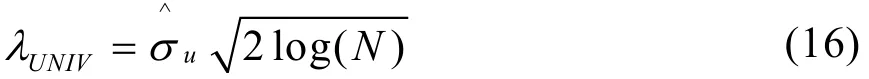
在阈值的确定过程中，将每一个分解尺度的高频信息量都看成是一个单独的信号源，将每一层高频小波系数分成n个相等的小区间，计算各个小区间的小波熵，选取熵值最大的那个小区间的中值作为该尺度下噪声的方差，再根据（16）式计算出各个尺度下的阈值，实现基于小波熵的阈值自适应选取。

3 基于小波熵的阈值确定法

采用舰船磁场仿真软件生成一组探测距离413 m的航空磁性探潜试验数据，如图1所示，从图中可以看出，目标信号完全被环境噪声湮没，无法进行分辨。基于Meyer小波基函数对一组信号进行5层的多尺度分析，得到的1～5层的细节信号，如图2所示。从图中可见，第1、2、3层细节信号的幅值较小，第4层细节信号的幅值有所增加，而第5层细节信号不但幅值增加，其包络曲线构成的低频成分和舰船磁场信号已非常相似。分别计算各层小波的功率谱，如图3所示。其中，第4、5层分解信号的功率谱值较大，集中在0.04 Hz～0.2 Hz的频带，主要成分是背景极低频磁干扰谱；第5层信号谱集中在0.03 Hz左右，目标信号包络清晰可见。小波变换大大的提高了在0.5 Hz以下低频段的频率分辨率，且很好的将中心频率各异的目标信号和背景信号分开来。但在0.05 Hz左右的位置信号叠加严重，必须选取合适的阈值进行滤波，才可以滤除幅值较大的背景噪声，提取目标弱信号。图4给出了基于不同阈值选取方法的小波去噪处理结果，其中（a）为采用固定软阈值的小波去噪结果；（b）为采用SURE方法确定阈值的小波去噪结果；（c）为采用极大极小阈值的小波去噪结果；（d）为利用小波能量熵确定阈值方法的小波去噪结果。从图中可以看出，基于小波能量熵的去噪结果明显要由于其他三种方法。

图1 目标信号和观测信号

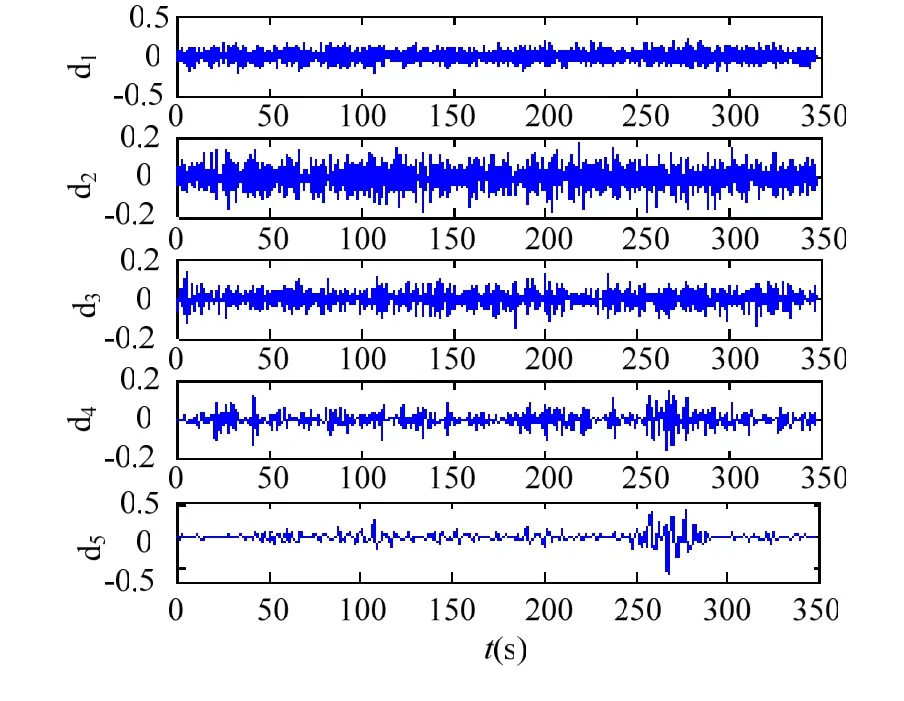
图2 目标磁场信号5层Meyer小波分析

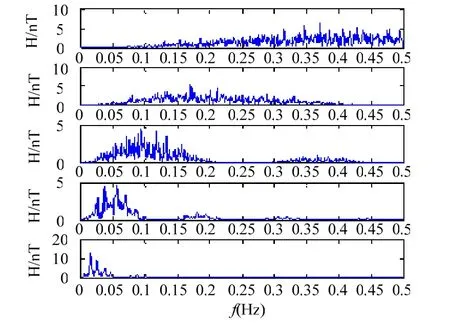
图3 各层小波的功率谱分析

图4 信号去噪结果

4 结束语

利用小波能量熵原理自适应地确定小波系数阈值的小波去噪方法，能够在较强背景噪声下实现对水下目标磁场信号的有效检测，仿真结果表明，这种检测方法能够有效地提高信噪比，对水下目标磁场信号位置进行较为准确的定位，有效地提取有用信息。

[1] 叶平贤, 龚沈光. 舰船物理场[M]. 北京:兵器工业出版社, 1992.

[2] D L Donoho and I M Johnstone. Journal of the american statistical association,1995,90（432）:1200.

[3] B K Alsberg,A M Woodward,M K Winson,et al.Analyst,1997,122（7）:645.

[4] 傅祖芸. 信息论——基础理论与应用. 北京:电子工业出版社,2001;24-25.

[5] Svaldo A Rosso, Susana Blanco, et al. Wavelet entropy: a new tool for analysis of short duration brain electrical signals. Journal of Neuroscience Methods,2001;105:65—75.

[6] Donoho D L, Johnstone I M. Ideal de-noising in an orthogonal basis chosen from a library of bases. C R Acad Sci I-Math.1994,319:1317-1322.

[7] Jansen M. Noise reduction by wavelet three holding.New York: Springer-Verlag, 2001.

[8] 吴正国, 夏立, 尹为民. 现代信号处理技术[M]. 武汉:武汉大学出版社,2002.

[9] 印欣运, 何永勇. 小波熵及其在状态趋势分析中的应用[J]. 振动工程学报, 2004, 17（2）: 165-169.

[10] 张荣标, 胡海燕, 冯友兵. 基于小波熵的微弱信号检测方法研究[J]. 仪器仪表学报, 2007, 28（11）:2078-2084.