参数辨识在船舶运动控制中的研究与应用

李光磊 臧涛 范邹 韩冰

（1. 海军驻九江地区军事代表室，江西九江 332007； 2. 海军蚌埠士官学校，安徽蚌埠 233012）

1 引言

船舵无疑是舰船各个部件中最主要部件之一，随着舰船控制舵的发展，船舵已经由手动操舵向自动舵方向发展，自动舵以其方便和实用越来越受到部队的重视和应用。理论上，只有预先掌握船舶运动规律的先验知识，如船舶参数、噪声参数等，才能设计出较理想的控制算法。

本文分别采用最小二乘法和遗传算法对船舶运动参数进行辨识，针对对比仿真存在的问题，根据最小二乘法和间接模型参考自适应法的特点提出一种基于两种方法的混合算法[1]。实验表明混合算法克服了原有单一算法针对非线性系统参数辨识的固有缺陷，辨识效果大大改进，因此对船舶参数辨识具有重要意义。

2 船舶运动方程的建立

要进行船舶的辨识和控制算法的研究，首先都必须建立船舶操纵运动的数学模型。考虑到船舶运动控制参数应尽可能少，同时兼顾船舶航行状态的可观测性，我们采用经典的非线性KT方程作为出船舶数学模型。

船舶运动KT方程是连续的微分方程。为辨识该连续方程，要求提供角速度乃至航向角加速度的输出值。但在工程实践中，很难正确测定上述运动参数，而且即使测定了航向角速度，它与航向测定值往往也不太匹配，同时航向的测定精度一般要求较高，故可用对航向角输出值进行数值微分的方法以提供上述运动参数[2]。

考虑一阶非线性船舶运动方程：

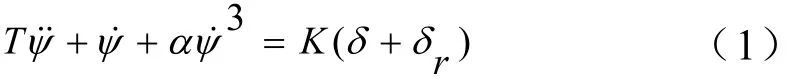
将其离散化为：

考虑二阶非线性船舶运动方程：

将其离散化为：

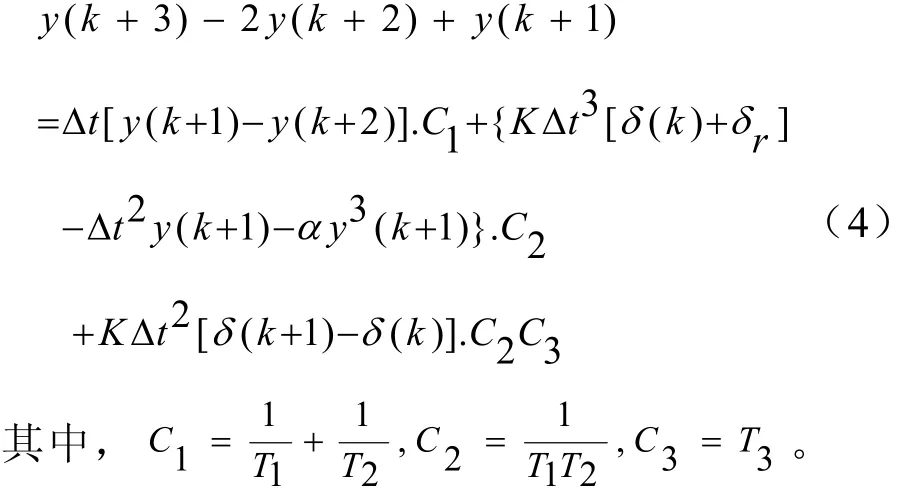
3 最小二乘法在船舶运动方程参数辨识中的应用

应用最小二乘法辨识原理对非线性模型的参数辨识需要对非线性模型进行一定的处理。现以二阶非线性方程为例来说明其应用原理[3]。

式（4）是经过处理过的非线性离散方程。

取Y=Φθ

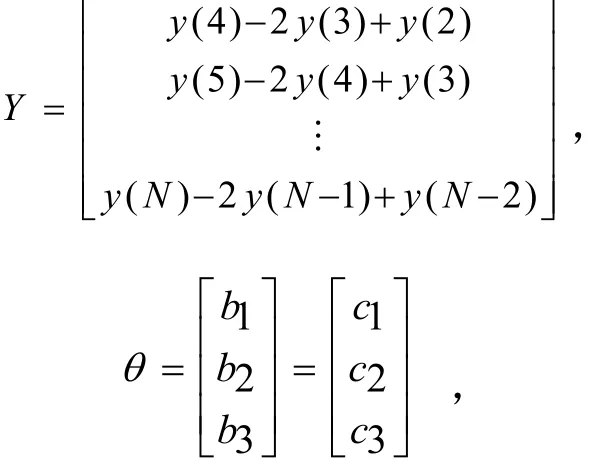
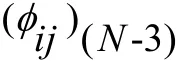
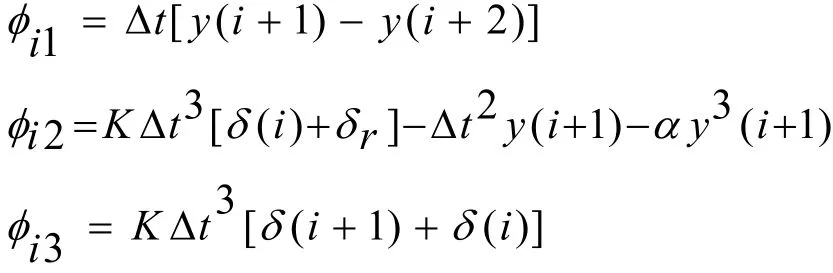
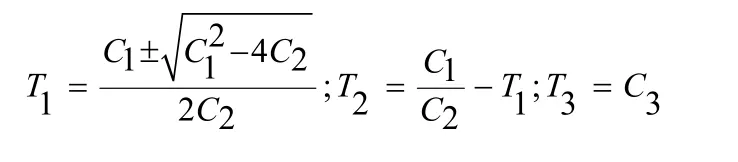
以上是基本最小二乘法在船舶运动方程中的应用，因为基本最小二乘法具有估计的有偏性，故可利用广义最小二乘法对参数进行估计。

4 遗传算法在船舶运动方程参数辨识中的应用

遗传算法来源于生物进化中“适者生存”的思想。通过模拟自然界进化中的自然选择，基因重组以及基因突变来进行自学习和寻优。基本遗传算法有选择、交叉和变异三个基本算子组成。具体过程如下：

（1）编码并生成初始种群。遗传算法不能直接处理解域中的数据，因此需通过编码将它们表示成遗传空间的基因型数据串，本文采用串联二进制编码。对于初始种群的个体，则是通过随机方法产生。

（2）计算适应度。适应度是遗传算法中的核心部分，它决定了种群中个体对所求解的问题的适合程度，在船舶运动方程中就是判定种群中变量即K、T是否符合方程。因此对适应度的设计就至关重要。

在这里我们根据船舶运动方程的特点，运用残差平方和对个体的适应度进行判定。下面以二阶方程进行说明。

对（4）进行变形得：

（3）选择、交叉和变异。采用基于线性排序的适应度分配的方法来进行选择操作。

交叉是提高遗传算法搜索能力的一个重要操作，在此我们采用离散重组的方法。由于自适应遗传算法在保持群体多样性的同时，也保证了算法的收敛性。

对交叉进行自适应的调整公式如下[4]：

其中：Pc1，Pc2分别为交叉概率的上限、下限；f1为要交叉的两个个体中较大的适应度；favg为每代群体的平均适应度；fmax为群体中最大适应度值。在此，我们选取Pc1=0.9，Pc2=0.6。

相应地，我们对变异操作也进行自适应操作。

对变异进行自适应的调整公式如下[4]：

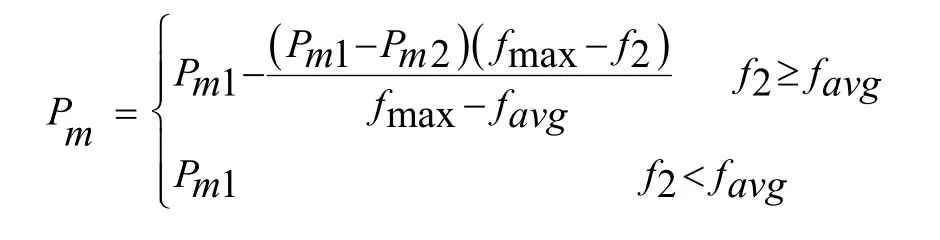
其中：Pm1，Pm2分别为变异概率的上限、下限；f2为要变异的两个个体中较大的适应度；favg为每代群体的平均适应度；fmax为群体中最大适应度值。在此，我们选取Pm1=0.1，Pm2=0.001。

（4）噪声处理

众所周知，在实际的船舶航行时采集的数据中噪声是不能不考虑的一个重要因素，因此在实际数据运算中就必须考虑对噪声进行处理。

在遗传算法的适应度函数中，我们选取（4）式的残差平方和作为适应度函数，其矩阵表达形式为Y=Φθ。

其中：

残差e（k）=Y-Φθ，但这一判定标准没有考虑噪声。然而实际中噪声是不可避免的。为此我们需要对噪声进行处理。

5 仿真试验

遗传算法是一种随机搜索法。它无需求导、理论上能全局收敛的解非线性模型参数估计的方法。遗传算法因其自身独有的优点，因而在解决非线性模型参数估计方面有着很大的优势。最小二乘法在辨识的参数比较多时，可能存在“参数相消”效应，即辨识所得的各参数同时偏离各自的真值，但只要它们和参数真值保持相同比值，同样可以是误差函数为最小。下面对非线性方程在数据无干扰情况下，应用遗传算法和最小二乘法进行仿真对比，其中遗传算法采用自适应遗传算法，即在基本遗传算法基础上加入交叉概率和变异概率自适应机制。

5.1 一阶非线性仿真比较

本实验使用的数据是根据大连海事大学的试验船“育龙”号的仿真结果进行的数据模拟[5]。K=0.478，T=216，α=30；除此之外，还对参数进行另外设定以检验辨识方法的优劣。对比实验数据见表1、2。

表1 最小二乘法实验数据记录表

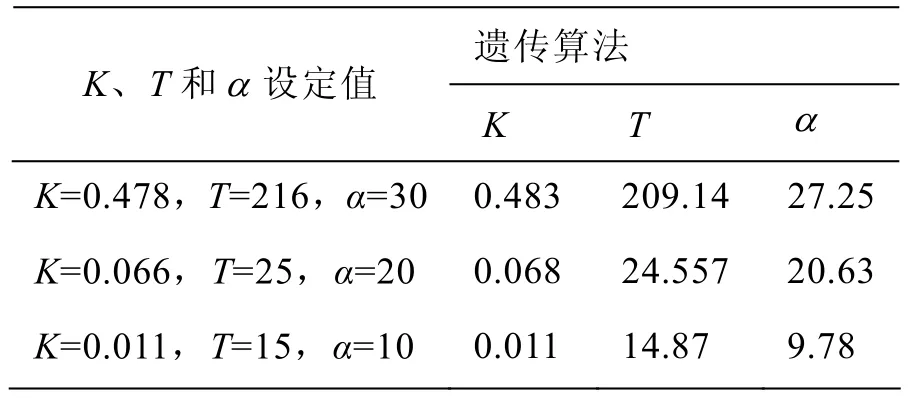
表2 遗传算法实验数据记录表

5.2 二阶非线性仿真比较

对比试验数据见表3、4。

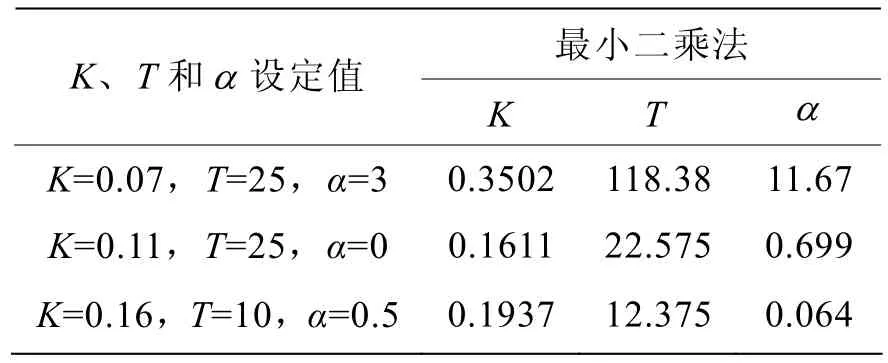
表3 最小二乘法实验数据记录表

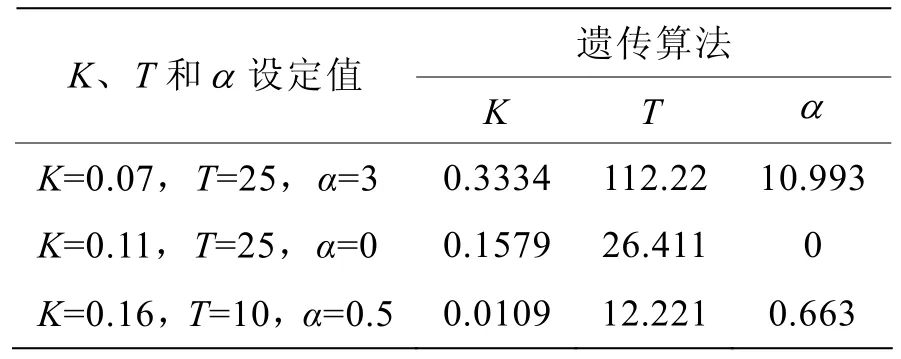
表4 遗传算法实验数据记录表

在K=0.07，T=25，α=3这一组数据中出现可参数相消现象。以上说明最小二乘法与遗传算法在辨识非线性系统且参数较多时，均存在着参数相消现象。最小二乘法仿真图见图 1，遗传算法K值进化过程见图 2。因此用这两种方法不能可靠辨识出二阶非线性方程的参数值。

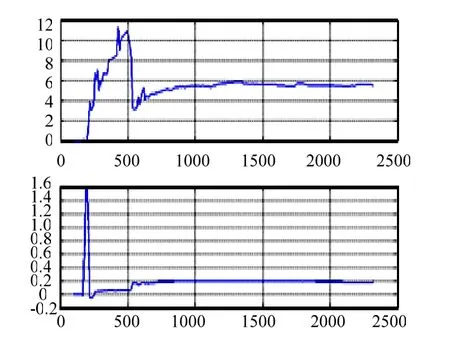
图1 广义最小二乘法仿真图

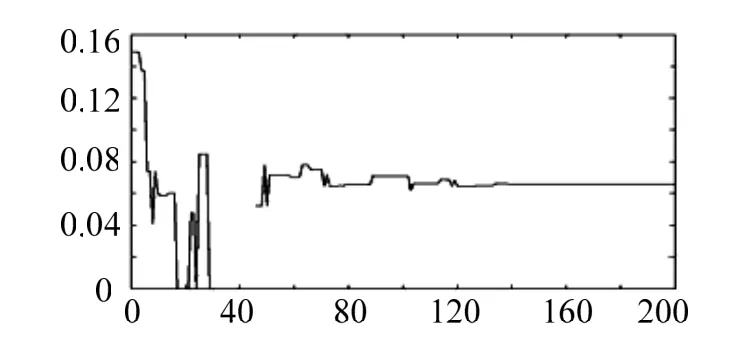
图2 遗传算法K值进化过程

二阶非线性方程的Simlink仿真图如3所示。

6 算法改进与仿真

我们知道间接模型参考自适应法具有很强的局部搜索能力，但它易于陷入局部最优解，且对初值的设定要求比较高，因此本文将介绍一种混合算法。由上面结果表明，最小二乘法与遗传算法在辨识低阶非线性模型能够大体辨识出参数的值，我们将根据其中一种算法辨识的参数作为初值，然后根据间接模型参考自适应法进行局部搜索。最小二乘法与遗传算法辨识的参数区别不大，但考虑到运算速度，我们将采用最小二乘法辨识参数的初值。

6.1 算法的实现

考虑野本一阶方程：

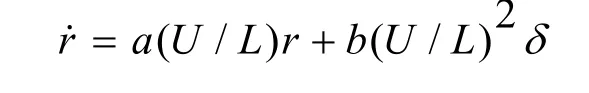
图3 二阶非线性方程的Simlink仿真

其中：r为航向变化率，δ为舵角，a=-1/T'＜0，b=K'/T'＞0，由间接模型参考自适应法的数学原理，设定P=1，自适应参数为：

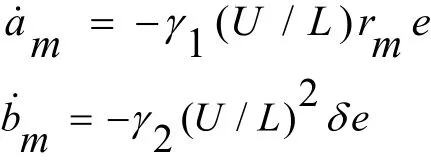
其中：e=rm-r，r为采集的实际数据；rm是推算的航向变化率，其表达式为：

其中h为采样时间。由于所要求取的参数a，b都很重要，因此权重系数设定为γ1=γ2=100。

用以上方法不断修改am，bm使其接近于真实值a，b。

下面编程实现船舶在无干扰下的数据生成，其中船长L=150 m，船速U=8 m/s，a=-0.6，b=0.2，K=0.01778，T=31.25，舵角信号为 3×sin（0.05×t）。试验是在采样时间为0.5 s、1 s、2 s三种情况下对参数进行辨识。实验数据记录见表 5。其中最小二乘法采用广义最小二乘法。

表5 实验数据记录表

图4是混合算法仿真示意图。

6.2 算法的仿真

图4 混合算法仿真示意图

由于在无干扰情况下混合算法辨识结果较好，故表6将考虑有噪声干扰情况下混合算法的辨识结果。其余数据与无干扰情况下的相同，当在图3的干扰模型中的白噪声能量设为0.01时。

表6 实验数据记录表

当在图3的干扰模型中的白噪声能量设为1时的实验数据记录见表7。

表7 实验数据记录表

由以上实验结果表明改进后的混合算法在船舶运行良好状态下对采样时间的要求不是很高，而对一般辨识参数要求对不同船型进行合适的采样时间的设定。由于我们常常无法准确地合理划分船型大小，因此，本方法对实际参数辨识意义重大。

7 结束语

本文首先根据最小二乘法和遗传算法的基本原理对船舶运动方程的参数辨识进行了仿真实验，通过对比试验结果可知，遗传算法能够较准确地辨识参数较少的低阶非线性方程，而在辨识参数较多的二阶非线性方程时出现了辨识参数相消的现象，不能够准确辨识出参数的真实值。结合上述现象，设计出一种基于最小二乘法和间接模型参考自适应法的混合算法，该算法对原有的单一算法进行了优化，仿真结果令人满意，为较好地解决非线性系统的辨识问题提供了一条有效途径。

[1] 韩冰. 舰船航行参数辨识的方法研究与实现[D]. 武汉:海军工程大学, 2008.

[2] 辛元欧, 俞胜芬. 关于K—T方程类的辨识方法研究——自回归模型的辨识[J]. 中国航海,1983,13（2）:28-43.

[3] 李言俊, 张科. 系统辨识理论及应用[M]. 北京: 国防工业出版社, 2003,50-76.

[4] 王小平, 曹立明. 遗传算法－理论、应用与软件实现[M]. 西安: 西安交通大学出版社, 2002: 73－74.

[5] 李铁三, 杨盐生, 郑云峰. 不完全驱动船舶非线性控制[J]. 交通运输工程学报, 2003, 3（4）：39－43.