基于频谱分析的运动模糊图像的参数鉴别

苏军

(南京航空航天大学计算机科学与技术学院，江苏南京210016)

在获取数字图像的过程中，由于设备或操作者的原因，易造成运动模糊，这是一种常见的降晰过程。如果在曝光瞬间，相机镜头和对象之间有相对运动，那么拍摄到的图像便是运动模糊图像。运动造成图像模糊的过程实质就是对原始图像进行多点平滑的过程，也就是一个像素与运动方向上的周围像素进行累加平均的过程，即模糊图像某一位置上的原像素值已经不是原来的值，因此观测图像往往在某一方向上有模糊的重影［1］。

建立图像复原模型的关键是确定运动模糊系统的两个重要参数［2］:一是运动模糊的方向θ;二是运动模糊的长度L。文中主要通过对运动模糊图像做频谱预处理，对频谱实施Radon变换确定运动模糊的方向θ，进而计算出运动模糊的尺度L。试验结果证明这种参数估计的方法准确，模糊图像复原效果良好。

1 运动模糊图像的退化模型

一般来说，图像的退化过程可以用以下的模型表示。

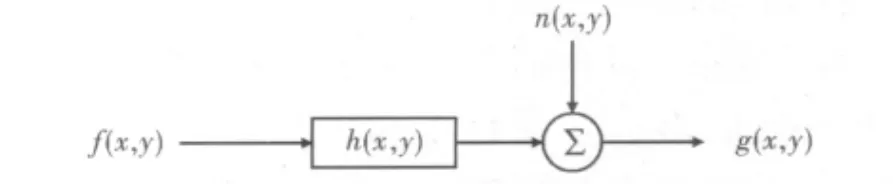
图1 图像退化模型

模型中h(x，y)和g(x，y)分别表示理想的图像和降质图像;则h(x，y)表示退化函数;n(x，y)表示各种噪音的集合，主要是指加性噪声。

因此，图像的降质现象可以用理想图像与点扩散函数的卷积过程来描述，公式表示如式(1)所示

由于曝光时间短，在这段时间内的相对运动可近似认为是匀速直线运动。因此观测图像往往在某一方向上有模糊的重影，这就为重建模糊模型提供了依据。

假设模糊图像的运动方向与x正轴成θ角度，运动距离为L像素，点扩展函数可以看作沿着x正轴旋转了θ角［3］，表达式如下

其中，x、y取值范围是

由上式(2)可知得，确定模型的关键在于准确的得出模糊尺度L和模糊角度θ。

2 运动模糊图像的参数估计

当目标图像和背景发生相对运动时，运动的方向可在倒频谱中体现出来［4］。由式(2)可得，点扩散函数的傅里叶变换表示为

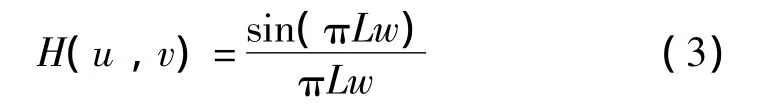
其中w=ucos(θ)+vsin(θ)，H(u，v)是个正弦函数，其零值发生在w=±1/L，±2/L，±3/L，…。

在忽略噪音的情况下，对式(1)做傅立叶变换，可得

因此，H(u，v)的零点也是G(u，v)的零点。

2.1 频谱中的方向特征

如果引起图像退化的点扩散函数具有零点，这些零点就会迫使退化图像的频谱在这些特点的频域上变为零。这将导致模糊图像的频谱也会在某些频谱上出现零点，表现在频谱上就会出现一系列暗线。根据上面得到的零点位置，可知运动模糊图像在频域上表现为一些垂直的等间距直线。

直接观察运动模糊图像的视觉效果差，因此为了精确提取出运动模糊图像的有效信息，采用Canny算子进行频谱图边缘检测，阈值的选取也直接影响频谱中方向的检测精度，选取阈值范围0.05～0.015。

Radon变换可以实现在某一特定方向上进行灰度累加，因此可以根据在一个［－90°，90°］的角度范围内求累加值，假设最大的累加值对应的角度是θ°，那么运动模糊的角度为θ－90°。

图2(a)中亮纹的走向验证了Randon变换。其中模糊尺度L是10像素，模糊角度θ=60°。

2.2 频谱中的长度特征

文献［5］中从理论上分析了模糊距离的频谱特点，即图像实际运动的距离与频谱图中暗线的数目有关，因此可以利用它来估计运动模糊长度。

图2 运动模糊图像

为便于直接观察图像频谱中的平行条纹，对频谱进行对数变换，对数变换的目的就是将原图像的频谱进行灰度压缩，使图像的条纹更加清晰，而其条纹间距不变。同时注意，由于对数变换的原因，应将式(4)中的零点替换为很小的正数。

考虑到Radon变换［6］的特点，可以使用求得的模糊角度θ，得到频谱在方向θ上的投影向量。频谱中心是低频部分，因此这个投影向量也会以中心为轴，两边对称分布，中间最宽的部分可看作两边的叠加，是两个峰值的叠加。如图3所示，模糊尺度L是10像素，模糊角度θ是60°的投影图，峰值的个数正好与模糊长度相等。

图3 方向上的Radon投影图

这里对于同一幅图像，只要模糊长度确定，任意的模糊角度，得到的Radon变换投影图都是相似的。

3 模糊参数的验证结果与分析

采用上述方法验证了本算法的有效性和适用性。针对仿真的和实际拍摄的模糊图像，应用本文提出的估计方法所鉴别出运动模糊参数，并用经典的维纳滤波复原运动模糊图像。

(1)仿真运动模糊图像，参数:L=17像素;θ=25°;方差为0.01的高斯噪声。鉴别出参数是L=17像素，θ=23°。复原效果如图4所示。

(2)实拍的运动模糊图像，应用提出的方法鉴别出模糊参数:L=10像素;θ=42°。复原效果如图5所示。

图4 仿真图像验证

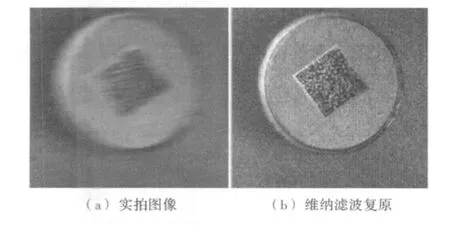
图5 实拍图像验证

运动模糊图像经维纳滤波复原后的效果，也进一步证实了提出的求解方法。

4 结束语

提出了在频域中应用频谱特点，研究运动模糊图像的点扩散函数参数的估计问题。结合Radon的数学特性鉴别出模糊参数，并给出了具体步骤。实验结果表明，根据PSF的模型参数进行维纳滤波复原验证了该方法的准确性。该算法具有易于理解和操作，适用性较广的优点，具有一定的研究价值。

［1］ LOK HANDE R，ARYA K V．Identification of parameters and restoration of motion blurred images［J］．Chinese Journal of Computers，2007，30(4):686－692．

［2］ YITZTMKY Y，KOPEIKA N．SIdentification of blur parameters from motion blurred images［J］．Graphical Models and Image Processing，1997，59(5):310－320．

［3］ 孙兆林．Matlab 6.x图像处理［M］．北京:清华大学出版社，2002．

［4］ CANNON M．Blind deconvolution of spatially invariant image blurs with phase［J］．IEEE Trans．Acoust．Speech Signal Process，1976，ASSP－24(1):56－63．

［5］ 郭永彩，郭瑞瑞．运动模糊图像点扩展函数的参数鉴别［J］．仪器仪表学报，2010，5(31):1052－1057．

［6］ FABIAN R，MALAH D．Robust identification of motion and out－of－focus blur parameters from blurred and noisy images［J］．CVGIP:Graphical，Models and Linage Processing，1991(53):403－412．