两点电荷电场中场强的极值点与单调性

李新良

（泰兴中学 江苏 泰兴 225400）

《物理通报》2010年第9期《两等量同号点电荷中垂线上场强的极大点》一文，通过逼近法找出了场强极大点．笔者认为虽然实践中可操作，但理论上不精确，而且不能反映场强变化的单调性．本文对几种电场的场强的极值点和单调性的判断进行了完整的数学推导，并用几何画板作图研究场强随空间位置的变化，使人们对单调性有直观感受．

1 等量同号点电荷中垂线上的场强

如图1所示，点电荷A，B带电荷量均为＋Q，相距2L，连线AB中点为O．中垂线上某点P的合场强为

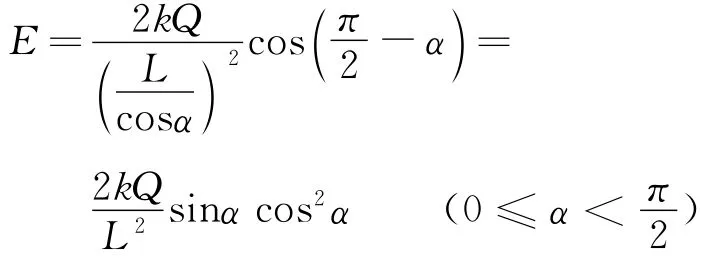
图1

先讨论极值，令f（α）＝sinαcos2α，求导可得

令f′（α）＝0，则有

查三角函数表知α＝35．264°，即α＝0．196π时中垂线上场强出现极值．再讨论单调性，由

可知，f′（α）的正负仅取决于（cosα－槡2 sinα）的正负．所以当0≤α＜35．264°时，f′（α）＞0，场强E单调递增；当35．264°＜α＜90°时，f′（α）＜0，场强E单调递减；当α＝35．264°时，f′（α）＝0，场强出现极大值．以上结论具有普适性．如图2，利用几何画板作出函数f（x）＝sin x cos2x的图像，在0～区间可以直观验证上述普适结论．

图2 几何画板1

2 等量异号点电荷连线之间的场强

如图3所示，点电荷A，B带电荷量分别为＋Q和－Q，相距2L，连线AB中点为O，连线AB之间有一点P，设PO＝l（0≤l＜L），则P点场强为

图3

经分析，AO之间场强E将随l的增大而单调增大．根据对称性，连线AB之间O点场强最小，离O越远，场强越大，这一结论也能由电场线疏密定性得出．如图4，以L为一个长度单位，利用几何画板作出函数的图像，在0～1区间单调递增，也能验证上述结论．

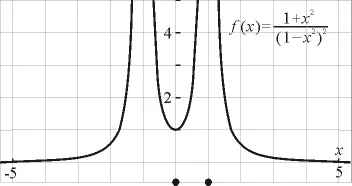
图4 几何画板2

3 不等量异号点电荷连线之外的场强

如图5所示，点电荷A，B带电荷量分别为＋Q，－q，相距L．现讨论直线AB上B点右侧各点的场强．B点右侧取一点P，以水平向右为正方向，则P点场强为

图5

引入函数

求导可得

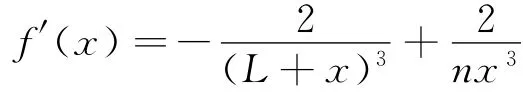
分别令f（x1）＝0，f′（x2）＝0．解得

因为n＞1，所以x2＞x1＞0，通过讨论f（x）、f′（x）的正负，并考虑到函数的单调性与矢量单调性的联系与区别，就能得到场强E的方向及单调性，结论见表1．

表1

由表1可知，场强极大值出现在x＝x2处．同样，以L为一个长度单位，取n＝4，则

如图6，利用几何画板作出函数f（x）的图像，能够对上述结论进行枚举法验证．

图6 几何画板3