模拟壳体/燃烧室外压承载能力研究
任 萍,侯 晓,何高让,来平安
(1. 西北工业大学 航天学院,西安 710072;2. 陕西动力机械研究所 固体火箭发动机燃烧、热结构与内流场重点实验室,西安 710025)
0 引言
固体火箭发动机在弹射、飞行等工况条件下,燃烧室作为火箭结构承力部件,要承受轴压、弯矩、外压等外载荷,而燃烧室壳体是主要承力部件,但是根据文献[1-3]的计算分析,壳体的外压承载能力相对较低;文献[4-5]从制造缺陷、结构方面开展了薄壁壳体外压承载能力的试验研究;文献[6-7]从缠绕参数、结构优化等方面提出了提高承载能力的途径,但远不能满足现有火箭特殊载荷工况的要求。壳体装药后,推进剂药柱是否可以提高壳体的外压承载能力,未见相关报道。
为了摸索推进剂对燃烧室外压承载能力的贡献,本文设计了缩比容器——模拟壳体和燃烧室,并开展了模拟壳体、燃烧室的外压试验,与此同时采用有限元软件分别进行了模拟壳体、燃烧室的外压稳定性计算分析。
1 模拟壳体/燃烧室外压试验情况
1.1 模拟壳体/燃烧室
模拟壳体由前后接头、前后裙和复合材料纤维缠绕结构组成,壳体直径200 mm,裙间距430 mm。燃烧室装药为贴壁浇注,药型为直通道中孔结构。模拟壳体、燃烧室结构见图1。

图 1 模拟壳体、燃烧室三维结构图Fig. 1 Three dimentional structure of simulated case and chamber
1.2 模拟壳体外压试验
用3个模拟壳体进行了外压试验。试验前模拟壳体前后裙用前后堵盖密封后置于标准容器内,采用水介质进行加载。外压加载程序为 0→0.5→0.8→1.0→1.1→1.2 MPa。试验过程壳体内部压力为0。
外压加载初期为均匀加载,3个试件分别加载到1.06 MPa、0.96 MPa、0.95 MPa时,试件发出一声响,随即压力显示降低,分别为0.68 MPa、0.79 MPa、0.74 MPa。应变测点的应变值随载荷增加而增大,达到失稳载荷时出现跳变。
从试验过程压力的降低以及应变值的跳变说明壳体已失稳,失稳载荷分别为1.06 MPa、0.96 MPa、0.95 MPa,平均0.99 MPa。
1.3 燃烧室外压试验
燃烧室外压试验方法同模拟壳体,也采用水介质加载。外压加载程序为 0→0.5→1.0→1.5→1.8→2.0→2.2 MPa→失稳。
试验加载过程中,载荷在2.0 MPa前压力上升速率基本相同。在2.0 MPa后加载压力上升速率减慢,到达2.26 MPa时(加载时间6 min),载荷突然降至0.157 MPa。试验后试件有一处明显内陷失稳痕迹,深约2 mm、长160 mm、宽5 mm左右,其位置在壳体中部。试验测得燃烧室的失稳载荷为2 MPa,与模拟壳体试验结果比较可见,燃烧室承受外压的临界载荷比壳体提高了一倍。
2 模拟壳体/燃烧室外压屈曲临界载荷计算
2.1 有限元模型的建立
根据模拟壳体/燃烧室实际结构,建立了壳体/燃烧室前后接头、前后裙、纤维缠绕结构以及药柱的实体模型,各实体模型的界面间为共节点单元,模拟壳体、燃烧室的有限元计算模型见图2。

图2 壳体和燃烧室有限元计算模型Fig. 2 Finite element model of case and chamber
边界条件:前裙端面限制所有位移和转动,后裙端面限制圆面内位移,轴向自由。
材料参数:壳体材料参数由实测单层板数据复合而成。药柱材料参数根据试验环境温度、加载速率,由实测松弛模量主曲线进行换算,同时考虑拉压载荷工况的差异,推进模量取6 MPa,泊松比为0.499。
2.2 计算结果
2.2.1 壳体计算结果
对图 2(a)中模型计算得到的模拟壳体线性临界外压屈曲载荷为1.66 MPa。一阶屈曲波形见图3,其中图3(a)为模拟壳体的整体屈曲波形,图3(b)为图3(a)变形最大处筒段中部的剖视图。模拟壳体外压一阶屈曲壳体母线方向变形半波数为1,壳体筒段环向变形波数为5。
在线性屈曲计算的基础上,将线性屈曲一阶模态乘以0.001叠加到初始结构,使原始结构有1 mm的初始几何缺陷,进行非线性屈曲计算。取壳体筒段表面径向位移最大值所在节点进行分析,其径向位移随载荷变化曲线见图4。在初始段位移随载荷呈线性缓慢增长,载荷达到一定值后出现拐点,载荷小幅增长,位移大幅增加。以位移增幅最大的点为失稳点,模拟壳体的失稳载荷为1.168 MPa,对应壳体壁表面的最大径向位移4.15 mm。

图3 模拟壳体一阶屈曲波形Fig. 3 The first buckle mode of simulated case under lateral pressure

图4 载荷-位移曲线Fig. 4 The curve of radial displacement vs. load
2.2.2 燃烧室计算结果
对图 2(b)模型计算得到的模拟燃烧室线性临界外压屈曲载荷为2.569 9 MPa,屈曲波形见图5,其中图5(a)为模拟燃烧室的整体屈曲波形,图5(b)为图5(a)变形最大处筒段中部的剖视图。模拟燃烧室外压一阶屈曲母线方向变形半波数为1,燃烧室筒段环向变形波数为5。
在线性计算的基础上,考虑初始缺陷进行非线性计算,计算方法同壳体计算方法。取燃烧室筒段表面径向位移最大值所在节点进行分析,其径向位移随载荷变化曲线见图6。在初始段位移随载荷呈线性缓慢增长,载荷达到一定值后出现拐点,载荷小幅增长,位移大幅增加。以位移增幅最大的点为失稳点,燃烧室的失稳载荷为2.012 MPa,对应燃烧室壁表面的最大径向位移为3.492 mm。
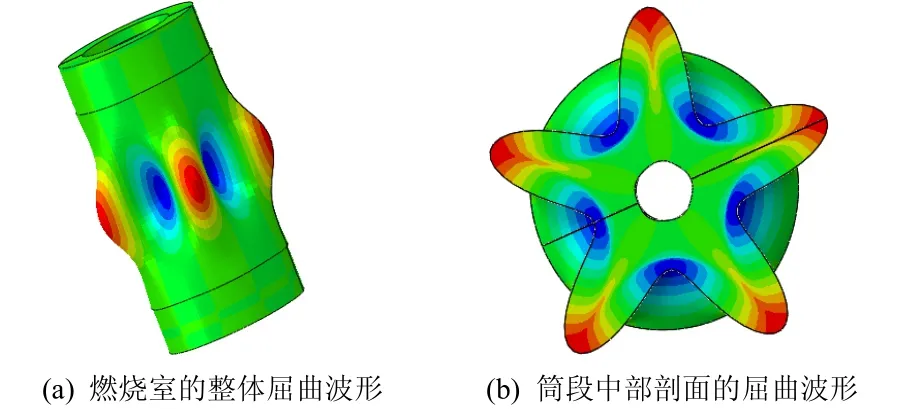
图5 模拟燃烧室一阶屈曲波形Fig. 5 The first buckling mode of simulated chamber under lateral pressure

图6 载荷-位移曲线Fig. 6 The curve of radial displacement vs. load
2.2.3 模拟壳体与燃烧室计算结果的比较
模拟壳体/燃烧室外压稳定性计算结果比较见表1。两者计算得到的一阶屈曲波形环向变形和母线方向变形相同,线性计算结果燃烧室的稳定性外压载荷是壳体的 1.55倍,非线性计算结果燃烧室是壳体的 1.72倍;非线性计算结果对应的壳体表面最大径向位移大于燃烧室表面径向位移。
为便于比对,图6还显示了壳体载荷-位移曲线,两者变化趋势一致:初始段载荷与位移呈线性变化,达到一定载荷后出现拐点,进入非线性段,载荷小幅增长,位移大幅增加。但拐点之后,燃烧室载荷-位移曲线明显高于壳体,相同径向位移燃烧室对应的外压载荷几乎是壳体的两倍。

表 1 模拟壳体/燃烧室外压稳定性计算结果Table 1 Calculated results for simulated case and chamber’s buckling load under lateral pressure
3 计算与试验结果的比较
计算结果与试验结果的比较见表2,可见模拟壳体/燃烧室非线性计算结果都与试验结果较吻合。计算和试验结果都表明药柱对燃烧室承外压能力贡献较大,模拟壳体装药后使得其外压承载能力提高1倍左右。

表 2 计算与试验结果比较Table 2 Comparisons between test and calculated results
4 结束语
1)通过模拟壳体和燃烧室外压载荷作用下的试验得到了模拟壳体、燃烧室的外压失稳载荷,两者对比表明:药柱对燃烧室外压承载能力贡献较大。
2)在线性计算分析基础上并考虑初始缺陷对模拟壳体和燃烧室进行非线性外压屈曲分析,较好地模拟了实际结构的外压承载能力,计算结果与试验结果较吻合。
3)燃烧室外压承载能力远大于壳体承载能力,因此在对发动机外压工况设计时,需要综合考虑壳体及其装药的承载能力,即整个燃烧室的承载能力。
(
)
[1] Jan de Vries. Analysis of localised buckling of cylindrical shell using a hierarchical approach, AIAA 2006-2274[R]
[2] 李志敏, 沈惠申. 三维编制复合材料圆柱壳在外压作用下的屈曲分析[J]. 固体力学学报, 2008, 29(1): 52-58
Li Zhimin, Shen Huishen. Buckling of 3d braided composite cylindrical shells under external pressures[J]. Chinese Journal of Solid Mechanics, 2008, 29(1): 52-58
[3] 王虎, 王俊奎. 复合材料圆锥壳体的外压稳定性[J].应用数学和力学, 1991, 12(12): 1087-1094
Wang Hu, Wang Junkui. Stability of laminated composite circular conical shells under external pressure[J]. Applied Mathematics and Mechanics, 1991, 12(2): 1087-1094
[4] Chiara Bisagni, Potito Cordisco. Test of stiffened composite cylindrical shells in the postbuckling range until failure[J]. AIAA Journal, 2004(9)
[5] Hilburger M W, Nemeth M P, Starmes J H Jr . Shell buckling design criteria based on manufacturing imperfection signatures[J]. AIAA Journal, 2006(3)
[6] 刘涛, 徐芑南, 裴俊厚. 复合材料圆柱壳的稳定性及其优化设计[J]. 中国造船, 1995(2): 12-21
Liu Tao, Xu Qi’nan, Pei Junhou. Buckling analysis and optimal design of composite cylindrical shells[J]. Shipbuilding of China, 1995(2): 12-21
[7] 谢禹钧, 邬柱, 刘占民. 混杂纤维缠绕圆柱壳外压稳定性与缠绕参数[J]. 复合材料学报, 1995(1): 106-110
Xie Yujun, Wu Zhu, Liu Zhanmin. Buckling strength and optimum parameters of hybrid fiber cylindric shells under external pressure[J]. Acta Materiae Compositae Sinica, 1995(1): 106-110

