应用史密斯圆图提取慢波微带线特征阻抗方法

董峦

（新疆农业大学 计算机与信息工程学院，新疆 乌鲁木齐 830052）

0 引言

在微波集成电路(MIC)或单片微波集成电路(MMIC)中，电路的小型化是优先考虑的设计目标[1-6]。慢波微带线可以提高所传导电磁波的相位常数β，进而缩短单位电长度微带线的物理长度，因此成为射频器件小型化的一种手段[2-6]。

慢波微带线的主要特性参量有特征阻抗Zc和相位常数β。相位常数可以直接测量，而特征阻抗需要通过间接手段获得。一般是先计算微带线分布参数和其不连续性引起的寄生参数[2-3]，然后通过(1)式计算。由于对寄生参数的计算是基于近似公式并且常常忽略相邻慢波单元的耦合，所以分布参数的计算结果存在误差，进而影响到特征阻抗的准确计算。测量镜像阻抗可以解决相邻慢波单元存在耦合时分布参数的计算问题[3]。

因为对特征阻抗的计算存在误差，所以在慢波微带线设计阶段就需要一种手段来评估计算结果。例如采用时域有限差分方法计算特征阻抗[7]，这种基于数值计算的方法需要较长的建模和计算时间；或者由测量的S参数提取特征阻抗[8]，这种方法较为简便。

还可以在电磁场仿真软件例如sonnet中对慢波微带线进行频率扫描，通过观测反射系数在史密斯圆图上的图像来提取特征阻抗。该图像是一个圆，圆的位置和直径说明了慢波微带线特征阻抗与目标特征阻抗的相对大小。从圆的特殊位置读出反射系数后就可以依据特定公式计算特征阻抗。以该方法提取慢波微带线特征阻抗简单易行，一个梳状慢波微带线的例子说明了提取结果的准确性。

1 提取特征阻抗

在仿真软件sonnet中，以图1配置搭建电路。若慢波微带线的目标特征阻抗是Z0，则连接它的微带线的特征阻抗和端口的阻抗都应设置为Z0，其长度可以任意选取只要慢波微带线距离仿真环境的边界足够远即可，这段微带线将在仿真中被去嵌入(De-Embed)。

参考面T上的反射系数是：

其中Zs、βs和ls是慢波微带线的特征阻抗，相位常数和长度。

图1 慢波微带线特征阻抗提取电路

对图1所示电路从较低频率（小于1MHz）进行频率扫描，在Smith圆图上绘出的反射系数图像是图2所示3种情况之一。当Zs=Z0时Γ=0，反射系数的图像是原点上一个点。当ZsZ0时，反射系数的图像是左半Γ平面或右半Γ平面的圆，圆的半径越大说明微带线特征阻抗与目标特征阻抗的偏差越大。(2)式可以解释在史密斯圆图中看到的图像，当以频率为自变量按(2)式绘制反射系数的极坐标图时得到的就是一个圆。当时

此时如果ZsZ0那么反射系数是图2中的B点。由(3)式得：

因此读出A、B点的反射系数后就可以用(4)式计算慢波微带线的特征阻抗。

图2 反射系数在史密斯圆图上的图像

2 验证测量方法

以图1配置搭建测量电路，其中慢波微带线是图3所示梳状慢波微带线。梳状慢波微带线可以看成高阻抗线和低阻抗线交替排列的结果[3]。

在sonnet中基板εr=2.3，tanδ=0，厚度是1mm，微带线采用理想导体，即认为没有导体损耗和介质损耗，这样的假设不影响对结果的讨论。对测量电路从1MHz扫描到13GHz，反射系数的图像是史密斯圆图中一个右半Γ平面的圆，由于图像与图2中Zs>Z0时的情形类似，这里省略。图像B点处的反射系数经线性插值计算得0.06287，根据(4)式计算出特征阻抗Zs=53.249Ω。

微带线的特征阻抗还可以通过其S参数提取[8]，公式是：

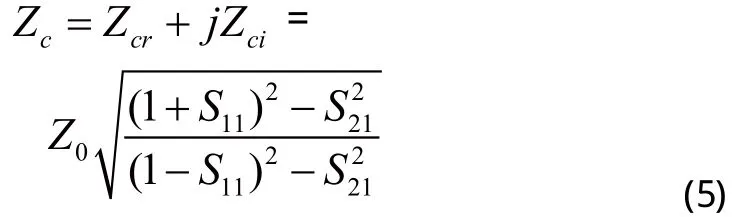
其中Zc是复特征阻抗。当微带线是无损线的时候，Zc是实数。

对原电路进行仿真得到一组S参数，按(5)式计算得到的特征阻抗显示在表1中。表1说明在不同频率点上都可以按(5)式计算特征阻抗，这些计算结果的差别十分微小，在高频时有一定下降。将梳状慢波微带线按本文方法提取的特征阻抗与表1的结果比较发现，两者非常接近，最大误差仅有0.14%。说明按本文方法得到的特征阻抗值是可以采用的。

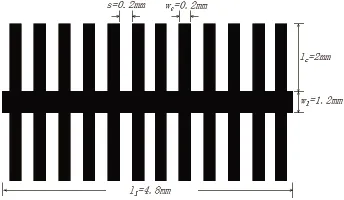
图3 梳状慢波微带线

表1 从S参数提取的梳状慢波微带线特征阻抗

3 总结

获得特征阻抗的准确值在慢波微带线设计中具有指导参数修改的重要意义，以上梳状慢波微带线为例，其特征阻抗提取结果大于设计目标50Ω，因此按照(1)式可以通过减小分布电感或增大分布电容来减小特征阻抗，对应到图3所示具体电路即增大wl或增大lc。

本文所述特征阻抗测量方法不仅适用于慢波微带线，还适用于常规微带线和人工微带线。该方法的优点是以直观的图像反映了慢波微带线特征阻抗的大小，有利于定性判断，并且特征阻抗计算公式简单，结果准确；缺点是提取的特征阻抗实际是慢波微带线电长度为π/2+nπ,n=0,1,2,...时的值，并且为了使反射系数图像到达史密斯圆图的A或B点，至少要频率扫描到使慢波微带线电长度变成π/2，若要形成闭合的圆则要扫描到使其电长度变成π，因此在电路规模较大时需要较长的仿真时间。

[1] 陈伟,张绍洲.慢波结构SIR双频带通滤波器设计[J].电子测试, 2010(6):66-70.

[2] K W Eccleston,S H M Ong.Compact planar microstripline branch-line and rat-race couplers[J].IEEE Trans. Microwave Theory Tech,2003,51(10).

[3] K O Sun,S J Ho,C C Yen,et al.A compact branch-line coupler using discontinuous microstrip lines[J].IEEE microwave wireless comp.lett,2005,15(8).

[4] Jae Jin Lee,Chul Soon Park.A Slow-Wave Microstrip Line With a High-Q and a High Dielectric Constant for Millimeter-Wave CMOS Application[J].IEEE Microwave Wireless Comp. Lett,2010,20(7):381-383.

[5] Jun He,Bing-Zhong Wang,Wei Shao.Compact microstrip power dividers with slow wave structure and capacitor loading[J].Microwave and Millimeter Wave Technology (ICMMT),2010:52-55.

[6] I-Tung Chou,Chia-Mei Peng,I-Fong Chen.A dualband Wilkinson power divider with microstrip slow-wave structures[C].Electromagnetic Compatibility (APEMC), Asia-Pacific,2010:723-726.

[7] M.-A.Schamberger,S.Kosanovich,and R.Mittra.Parameter extraction and correction for transmission lines and discontinuities using the finite-difference time-domain method[J].IEEE Trans.Microw.Theory Tech,1992,15(4):483-490.

[8] W R Eisenstadt,Y Eo.S-parameters-based IC interconnect transmission line characterization[J].IEEE Trans. Compon.,Hybrids,Manuf.Technol, 1992,15(4):483-490.