直升机桨距调节助力器电液加载系统的 H∞控制
刘国建 李运华 郑 琦 郭中伟
(北京航空航天大学 自动化科学与电气工程学院,北京 100191)
直升机桨距调节助力器电液加载系统的 H∞控制
刘国建 李运华 郑 琦 郭中伟
(北京航空航天大学 自动化科学与电气工程学院,北京 100191)
基于对某直升机桨距调节液压助力器地面试验用电液负载模拟器的原理分析,建立了电液加载系统的动态模型.由于电液加载系统中存在着结构参数难以精确获取和伺服阀负载流量非线性等不确定性因素,采用传统的经典控制理论设计出的控制器难以奏效,为此研究了基于 H∞理论的电液加载系统的鲁棒控制策略.选择适当的权函数,利用混合灵敏度的方法设计并且采用基于线性矩阵不等式的算法求解出鲁棒控制器.给出了使用鲁棒力控制器的试验结果,结果证明所设计鲁棒力控制器的有效性和优越性.
电液负载模拟器;力控制;鲁棒控制;混合灵敏度
桨距调节液压助力器是直升机主桨和尾桨操纵系统的关键部件,其功能是承受桨叶传递过来的气动载荷并使桨距跟随操纵杆的位移连续变化,它的性能直接影响操纵系统的整体性能.与固定翼飞机不同,直升机操纵面的气动载荷是交变的,频率较高且呈现高频大动载特征,从而导致加载系统的参数在大范围内变化.这种被控对象参数的大范围变化会加剧多余力补偿的难度,降低系统的控制精度和鲁棒性.因此,如何抑制多余力,是设计直升机桨距调节助力器地面实验电液加载系统中必须解决的关键问题[1-2].
本文结合助力器电液加载系统的机理和液压控制理论,建立了电液加载系统的数学模型,并将多余力作为系统的外干扰,使系统转换成 H∞控制的标准形式;通过分析电液负载模拟器加载系统中的不确定性,选取恰当的权值函数,采用混合灵敏度的方法,求解出基于 LMI(Linear Matrix Inequality)的 H∞鲁棒控制器.
1 加载系统描述
直升机桨距调节液压助力器的电液伺服加载系统如图 1所示.操纵助力器(由 1~4组成)实现操纵杆位移规律的模拟;桨距调节助力器 10通过连杆 12与桨距操纵杆连接;右侧为电液加载系统,通过力传感器与液压助力器的活塞杆连接.
工作过程如下:伺服位移系统带动助力器按照一定规律跟随指令信号运动.在伺服位移系统输入指令信号瞬间,加载系统的输入信号为 0,加载液压缸的两个工作腔封死,其活塞杆在被加载对象运动趋势的作用下,力传感器输出力信号不为 0,这个力就是多余力.力传感器检测到的力信号反馈给加载系统,控制器控制加载伺服阀使其产生开口,使得加载液压缸与助力器一起运行,多余力也随之减小.加载油缸输出的力包括:①在指令信号作用下的希望输出力;②由于助力器主动运动,在加载缸两腔产生强迫流量而引起的负载压力变化产生的多余力,其值很大,有时甚至超过希望力的值,因此需要采取机液或控制方面的措施加以消除.本文主要研究基于控制的抑制方法.

图1 桨距液压助力器实验用电液加载系统
2 电液加载系统数学模型的建立
1)加载端伺服阀的负载流量方程.假定阀为理想四通滑阀,且节流窗口是匹配对称的,阀的线性化流量方程为

式中,qL为阀的负载流量,m3/s;Kq为伺服阀的流量增益,m2/s;xV为阀芯位移,m;Kc为伺服阀的流量压力系数,m5/(N·s);pL为负载压力,N/m2.
2)加载端液压缸流量连续方程为

式中,Am为液压缸活塞有效面积,m2;Vm为液压缸总容积,m3;Csl为液压缸总泄漏系数,m5/(N·s);βe为容腔内液压油有效体积弹性模量,N/m2.
3)加载端的液压缸和负载的力平衡方程为
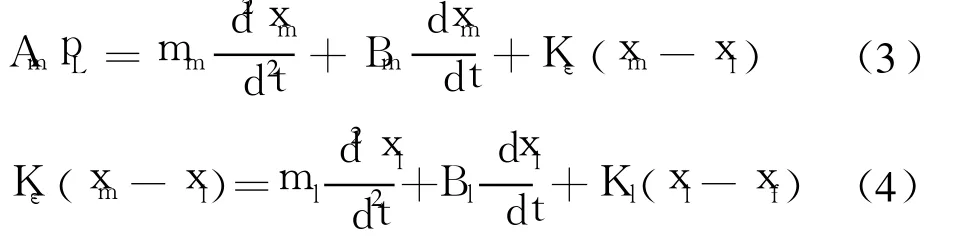
式中,mm为加载端活塞质量,kg;Bm为加载端活塞及负载的粘性阻尼系数,N·s/m;Kε为力传感器弹性刚度,N/m.
负载模拟器的输出为
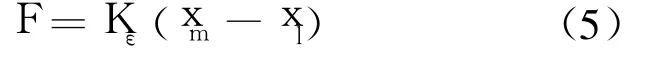
把力传感器看成弹性环节,根据式(1)~式(5),得动力结构输出力的传递函数:
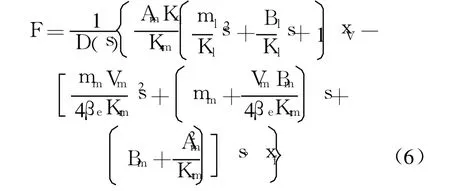
式中
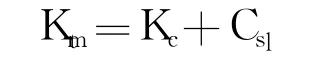

4)加载端电液伺服阀的传递函数[3]按一阶惯性环节处理,其表达式为
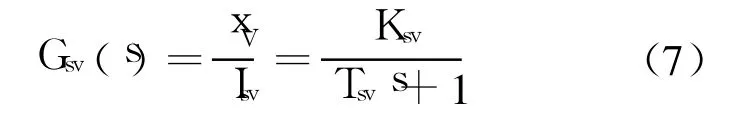
式中,Ksv为伺服阀阀芯位移驱动系数,m/A;Tsv为伺服阀的时间常数.根据前面的数学模型,电液负载模拟器总的方框图如图 2所示.
当系统主动加载时,即加载对象固定或者输入为 0(xf)的信号,可得无扰的系统开环传递函数如式(8).此时系统成为主动式力加载系统.

图2 负载模拟器控制系统方框图
式中,KF为力传感器增益,V/N.
3 基于 H∞控制理论的控制器设计
电液负载模拟器系统的不确定因素主要来源于参数变动、未建模动态、多余力及外干扰影响[4].考虑到本系统既要消除各类不确定性的影响,又要满足一定的性能指标,因此采用 H∞混合灵敏度设计方法来设计控制器 K(s).
3.1 近似模型的选定
当参数发生变化时,系统的频率特性会发生很大的改变.负载等效连接弹簧刚度变化范围一般在 3.5×106~1.7×107N/m之间,但弹簧刚度变化时只影响系统的低频和中频特性,对于系统的高频特性没有影响[5].
采用主导极点的方法对模型进行简化,把分母高频谐振频率去掉,使系统由五阶降为三阶:

式中
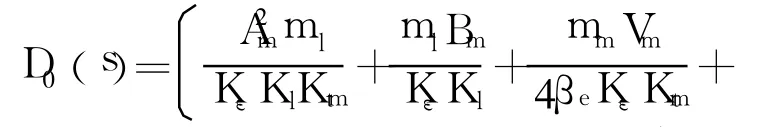

标称模型中的弹簧刚度取 7.8×106N/m,把相应的参数值代入式(9)得
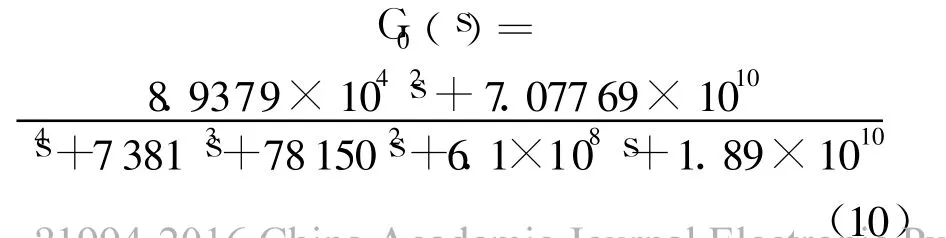
3.2 加权函数的选择及 H∞控制器的设计
H∞控制在很大程度上取决于加权函数的选择,所以选取适当的加权函数非常重要.
1)加权函数 Ws(s)代表了干扰的频谱特性,使其具有低频高增益的特性,可增强干扰的抑制能力[6],故此系统灵敏度加权函数选取为

2)控制器输出约束加权函数 WR(s)起到对控制器输出限幅的目的,本系统取

3)权函数 WT(s)是不确定函数,由模型的非结构不确定性即高频未建模动态和模型参数不确定性所决定,反映了被控对象本身的固有特性,WT(s)一般要求高通性质.WT(s)其阶次不宜取得太大,否则将影响迭代速度及控制器的阶数.选择补灵敏度加权函数为

使用 Matlab中 LMI工具箱的 hinflmi命令可以求解得到一个八阶控制器,为了便于模拟控制实现或计算机实现,将其降阶,得到控制器降阶模型:
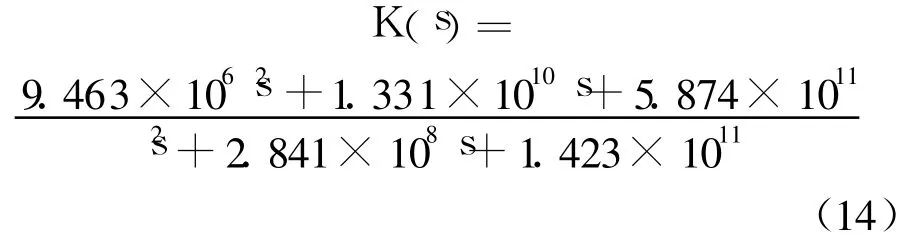
图3中灵敏度函数和补灵敏度函数都在其相应的权函数下面,说明满足鲁棒性和鲁棒特性.
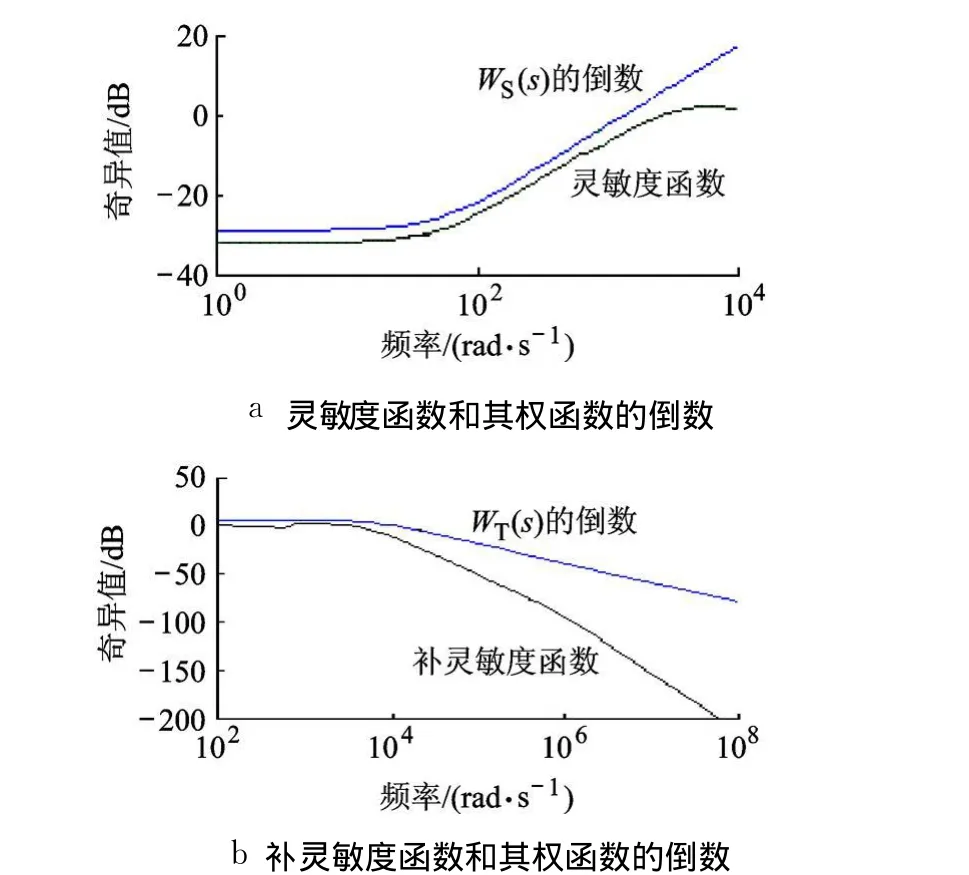
图3 奇异值响应
4 试验结果及分析
在所开发的电液加载与伺服操纵试验台上进行鲁棒力控制策略的研究.试验台的加载部分和伺服位移系统采用一个恒压式变量泵供油,系统压力为 15MPa;液压助力器采用专门的高低温恒压源供油,系统压力为 20MPa.试验中分别采用基于经典的结构不变性加校正控制策略和本文设计的鲁棒控制器.在伺服位移端给助力器输入幅值为 15mm和频率为 1Hz的正弦信号,使助力器始终做正弦运动;同时通过不同的加载力和加载频率给出了系统输出情况,考察系统鲁棒性.加载试验曲线如图 4所示.

图4 实际加载力与给定力曲线比较
从图 4中可看出,鲁棒控制器的输出信号 F明显好于经典控制器的输出信号,尤其是在高频加载下,即有干扰力时,效果更明显;经典控制器在高频加载时的效果明显下降;说明鲁棒控制器对系统不确定性的影响表现出更好的鲁棒性.
5 结束语
建立了电液负载模拟器的精确数学模型,针对电液负载模拟器中不确定性的因素,通过选择恰当的权函数,并通过 H∞控制的 LMI算法求解出控制器.试验结果表明:当采用传统的结构不变性原理补偿时,只补偿了与助力器速度有关的多余力,而与助力器加速度有关的多余力并没有补偿;低频被动加载取得了非常好的效果;高频加载时与助力器加速度有关的多余力增大,加载精度降低.
References)
[1]李运华,焦宗夏,王占林.舵机力矩负载模拟器的混合控制方法研究[J].航空学报,1998,19(7):62-67 Li Yunhua,Jiao Zongxia,Wang Zhanlin.Research on hybrid control method of moment al load simulator of actuator[J].Journal of Acta Aeronautic et Astronautica Sinica,1998,19(7):62-67(in Chinese)
[2]Prut Nakkarat,Suwat Kuntanapreeda.Observer-based backstepping force control of an electrohydraulic actuator[J].Journal of Control Engineering Practice,2009,17(8):895-902
[3]Wang Jingfu,Liang Lihua,Zhang Songtao.Application of H∞control based on mixed sensitivity in the electro-hydraulic load simulator[C]//Proceedings of IEEE.International Conference on Mechatronics and Automation.Harbin,China:Inst of Elec and Elec Eng Computer Society,2007:2991-2996
[4]吴凌尧,李文章,郭雷.具有非线性扰动与外部干扰的结构系统鲁棒H∞控制器[J].东南大学学报,2008,38(2):324-328 Wu Lingyao,Li Wenzhang,Guo Lei.Robust H∞control for structural systems with nonlinear perturbations and exogenous disturbances[J].Journal of Southeast University,2008,38(2):324-328(in Chinese)
[5]Dinh Quang Truong,Ahn Kyoung Kwan.A study on force control of electric-hydraulic load simulator using an online tuning quantitative feedback theory[C]//COEX.International Conference on Control,Automation and Systems.Seoul,Korea:Inst of Elec and Elec Eng Computer Society,2008:2622-2627
[6]李阁强,赵克定,袁锐波,等.μ理论在电液负载模拟器中的应用[J].航空学报,2007,28(1):228-233 Li Geqiang,Zhao Keding,Yuan Ruibo,et al.Application ofμ theory in electrohydraulic load simulator[J].Journal of Acta Aeronautic et Astronautica Sinica,2007,28(1):228-233(in Chine)
(编 辑:刘登敏)
Application of H∞theory in electro-hydraulic loading system of helicopter pitch adjusting booster
Liu Guojian Li Yunhua Zheng Qi Guo Zhongwei
(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
A dynamic model of electric-hydraulic loading system was established based on the principle analysis of electro-hydraulic load simulator,which was applied to the earth-experiment of hydraulic as sistor for the helicopter pitch adjusting.Controllers designed by conventional control theory were not effectual because of the uncertain factors such as difficulties in access to precise structure parameters of electric-hydraulic loading system and nonlinearity of loading flux in servo valve.Therefore the robust control strategy of electric-hydraulic loading system based on H∞theory was investigated in this work.Through choosing suitable weight functions and using the designing method of mixed sensitivity,the robust controller was solved by the linear matrix inequality(LMI)algorithm.The experiment results prove the high efficiency and superiority of the robust force controller which is presented by this work.
electro-hydraulic load simulator;force control;robust control;mixed sensitivity
V 217+.3
A
1001-5965(2011)02-0140-04
2009-12-01
航空科学基金资助项目(2009ZD 51040)
刘国建(1981-),男,山东菏泽人,博士生,jianchengliu@163.com.

