基于路段流量相关性的检测器优化布设*

王殿海 徐程 祁宏生 金盛

(1.吉林大学交通学院，吉林长春130022;2.浙江大学建筑工程学院，浙江杭州310058)

路网交通信息对于长期规划及短期预测都具有重要意义，路网交通信息的有效获取是实现交通管理与控制的前提与基础.目前，固定检测器依然是获取路网交通信息的重要手段之一，固定检测器的布设密度及位置都会直接影响采集交通信息的数量与质量.一方面，密集的检测器布设策略可以获取更多的交通信息，实现更加精细化的交通管理;另一方面，由于路网规模的不断扩大及交通基础设施的建设成本要求，路网检测器布设规模受到制约.因此，如何通过固定检测器的优化布设，用最少成本完成必要交通信息的采集就成为一个重要的研究方向.其核心思想就是:基于路网中各路段交通参数(特别是流量信息)之间存在相关性的事实，利用部分路段交通信息来推算全路网交通信息，以此达到优化检测器布设的目的，从而节约投资成本.

近年来，国内外许多学者致力于研究通过部分路段检测器信息获取全路网交通信息，以达到优化固定检测器布设的目的.根据获取信息类型的不同，可将现有研究成果主要分为两类，第一类是以获取起讫点(OD)信息为目的的检测器优化布设方法.在这方面，周晶等［1］提出了交通检测点合理分布的4种规则，并在已知OD对间有效出行路径的条件下，建立了确定最佳检测点的数学规划模型，提出了有效的启发式算法;Yang等［2］提出了基于Screen-Line方法的检测器布设模型及运算法则，分析了在给定检测器数量条件下如何布设能覆盖最多的OD对以及能覆盖所有OD对的检测器最佳数量及布设位置.Mínguez等［3］提出了不同情况(如完备路径识别性、最大路径识别性等)下用于推算OD信息的检测器最佳布设方法.第二类是以获取全路网流量信息为目的的检测器优化布设方法.在这方面，Bianco等［4］提出了一种为获得全路网交通流量所需检测器的最少数量及布设位置的方法，并确定了任意给定路网检测器布设数量的最高及最低限;伍建国等［5］通过对城市道路网基本路段交通流量的相似性分析，建立了路网交通检测器优化布点的数学模型;Castillo等［6-7］提出了基于贝叶斯网络的交通流预测方法及避免路径列举的检测器布设方法.这些研究成果为路网固定检测器优化布设提供了完善的理论支持，但由于上述方法需要较多的先验信息，且模型较为复杂，难以在实际中应用.

文中以获取路网流量信息为目标，在考虑路网拓扑结构和出行路径选择对检测器优化布设影响的基础上，提出了一种基于路段间流量相关性［8］的检测器优化布设方法，综合考虑检测器布设的多种影响因素(重点考虑路径覆盖率、道路等级、道路长度以及配套设施对布设结果的影响)，通过多目标优化获得检测器最优布设路段组，达到用最少的检测器获得全路网流量信息的目的，使之更加符合实际情况.

1 模型的建立

交通路网是一个由若干个路段及路网节点(交叉口)组成的有机整体.由于路网中的车辆在每个交叉口处的流向不同，每个路段的交通量存在差异性.但是，每个路段上的流量都是由经过此路段的所有路径流量组成.因此，各个路段间的流量会存在一种线性相关性.如果某些路段流量可以由其他路段流量线性表示，那么这些路段就不需布设检测器，而由其他路段流量推算得出其流量.因此，文中的研究重点就是确定需要布设检测器的路段集合，这里称之为关键路段集合.

1.1 交通路网描述模型

通常，一个典型的交通网络可表示为G(V，E).其中V表示路网内节点的集合，V={v1，v2，…，vs}，s为节点数;E表示路网中所有路段的集合，即E= {e1，e2，…，en}，n为路段数;W表示路网中OD对的集合，W={w1，w2，…，wt}，t为OD对数量;R为OD对间所有有效路径的集合，R={r1，r2，…，rm}，m为有效路径的数量.这里定义的有效路径都为简单路径［9］，即序列中顶点不重复出现的路径.R'为优选路径的集合，即每个OD对间出行费用最小的k条最短路径的集合，且R'⊂R.

为了描述路径及路段之间流量的相关性，采用路径流量矩阵、路段流量矩阵进行表达.路径流量矩阵定义为P=(p1，p2，…，pm)，pi(i=1，2，…，m)表示第i条路径的流量;路段流量矩阵定义为F=(f1，f2，…，fn)，fj(j=1，2，…，n)表示第j条路段的流量;路段邻接关系矩阵定义为As×s，矩阵中元素axy定义为

式中:ρ为出行费用;x，y=1，2，…，s.

路径－路段发生矩阵Lm×n定义为

式中:lij=1表示路径i经过路段j，lij=0表示路径i不经过路段j.

通过上述路径－路段发生矩阵的建立，就可以描述路径流量与路段流量之间的相关性.

1.2 关键路段数量的确定

假设关键路段(即布设检测器的路段)的集合为EI，关键路段间的流量线性无关.非关键路段的集合为ENI，它的流量可通过关键路段检测出的流量推算而得.且E=EI∪ENI，路径与关键路段的发生矩阵为，路径与非关键路段的发生矩阵为，b为关键路段的数量.

在线性代数中，对于向量组A:α1，α2，…，αn，如果存在A的部分向量组A0:αj1，αj2，…，αjr，满足A0线性无关A中任一向量可用A0线性表示，则称A0是A的一个极大线性无关向量组，简称极大无关组.极大无关组所含向量个数r称为A的秩［10］.通过这个定义可知，由于关键路段上的流量线性无关，路径与关键路段的发生矩阵中的列向量线性无关，路径与非关键路段的发生矩阵中的任意列向量均可由中的列向量线性表示，所以关键路段的数量就等于路径－路段发生矩阵的秩，且路径－路段发生矩阵的任一极大无关组即为此路网的一个关键路段组.

因此，将路径－路段发生矩阵Lm×n进行初等变换，可得到简化后的矩阵为

则关键路段的数量b=rank(L'm×n)即为此路径－路段发生矩阵的秩，而αi，i=1对应的路段即为关键路段，此矩阵的极大无关组即为关键路段组.根据线性代数中的知识可知，构成极大无关组的列向量个数是一定的(即秩数)，而矩阵的极大无关组不是唯一的［10］.因此，需要通过一定的规则筛选出所需的唯一极大无关组，那么这个路网中关键路段的数量和位置就能够确定.

1.3 关键路段数的影响因素分析

不同的路网规模及拓扑结构、不同的出行路径选择行为都会对关键路段的数量(即路径－路段发生矩阵的秩)产生影响.本节通过分析网络规模、网络连通性、OD对数量t及路径数量对关键路段数的影响，为路网检测器优化布设提供参考依据.

1.3.1 网络规模

网络规模是指路网内所含节点(交叉口)及路段的数量.对于同一种路网拓扑结构，节点数或者路段数的不同都会对关键路段的数量产生影响.为说明问题，此处以表1所示“田”字网络为例.网络规模越大，网络越复杂，路径的覆盖率越大，路段间流量的相关性越强，所以关键路段与总路段的比例b/ n减小.网络中的OD对集合为W={v1－v9，v9－v1}.

表1 网络规模与关键路段数的关系Table 1 Effect of network scale on the number of key links

1.3.2 网络连通性

连通性是图论中的一个重要概念.如果图G中存在vx－vy路径，则认为两个顶点vx和vy在G中是连通的.如果G中的每对顶点之间都至少存在一条路径，则图G是连通的.在图论中，与顶点vx关联的边数称为vx的度，记为d(vx)［9］.

在交通网络中，连通性对关键路段的数量具有影响，尤其是OD点的连通性对关键路段数的影响更为明显.为说明问题，此处以“田”字网络为例，如表2所示.对于同一种网络拓扑结构，当网络的连通性增强时，特别是当OD点间的连通性增强时，路段间流量的相关性也加强，因此关键路段的数量减少，关键路段与总路段的比例b/n也相应减小.网络中的OD对集合为W={v1－v9，v9－v1}.

表2 网络连通性与关键路段数的关系Table 2 Effect of network connectivity on the number of key links

1.3.3 网络中OD对的数量

在交通网络中，OD对的数量是个非常重要的因素.OD对越多，可选择的路径数量越多，路段之间的相关性越复杂.因此，OD对的数量对关键路段的影响尤为重要.对于同一种网络，当只改变OD对数量时，关键路段的数量随着OD对数量的增加而增加，关键路段与总路段的比例b/n也相应增大.此处以表3所示“田”字网络为例.当OD对数量足够多时，关键路段的数量会趋于某个定值b=19，即此网络固定检测器的最佳布设数量为19.

表3 网络中OD对的数量与关键路段数的关系Table 3 Effect of the number of OD pairs on the number of key links

1.3.4 网络中OD对间路径的数量

在实际路网中，节点(交叉口)及路段的数量往往很多，道路网的拓扑结构也很复杂，因此每个OD对间的出行路径会很多.在用此方法给实际路网布设检测器时，如果将每一个OD对间的所有有效路径都挑选出来，则计算量太大，运算时间过长.文中考察OD对间选择的路径数量对关键路段数的影响，目的在于验证此方法运用于实际路网时是否可以选择每对OD对间最短的k条路径，以获得最优的布设方案.

在选择路径时，优先选择最短路径.如表4所示，方案1为选择每个OD对间最短的两条路径，方案2为选择每个OD对间最短的4条路径，依次递推，直至选择所有有效路径为止.在此列举的为一“田”字型网络，OD对的数量为6，有效路径总数为66.当选择的路径较少时，关键路段的数量也较少.因为选择的路径不能经过网络中的所有路段，那些未被经过的路段就相当于被剔除掉了.当选择的路径数量增加时，关键路段的数量也相应增加，最后达到一个定值b=19，此定值即为这个交通网络的检测器布设最佳数量.因此，从这个影响因素可以得知，此方法正确及最优的前提是保证路网中的每一条路段都被走过一次.当OD对数量较多时，可以选择最短的k条路径进行检测器布设，减少运算复杂度，也更加贴合实际，k值可根据实际路网情况选取.网络中的OD对集合为 W=.

表4 路径数与关键路段数的关系Table 4 Effect of path number on the number of key links

1.4 最优关键路段组的确定

在确定关键路段的数量之后，重点在于如何在众多关键路段组集中确定最优关键路段组来布设检测器，这样就需要一些规则对关键路段组集进行筛选以确定最优的布设方案.在实际路网中布设检测器时，很多因素都会对最后的布设结果产生影响.例如，对于高等级路段或者高流量的路段，都希望尽量在这些路段上铺设检测器直接采集数据，以提高关键路段的数据检测精度;对于附近有配套设施的路段，也希望能尽量在该路段布设检测器，以便能充分利用现有资源，降低成本［5］.除此之外，道路长度、网络的拓扑结构、道路的敏感程度、检测数据的用途等都会对检测器的布设产生影响.因此，对于最优关键路段的选择，需要考虑多因素的影响.文中提出了考虑路径覆盖率、道路等级、道路长度、配套设施4种影响因素的多目标优化模型来确定最优布设方案，也可根据实际情况增加影响因素.

1.4.1 多目标优化模型

最优关键路段组的多目标优化函数为

式中:z1为路径覆盖率，即所选关键路段集经过的路径数量和与路网中所有路段经过的路径数量和之比，可以表示为

z2为道路等级比.即所选关键路段集中应包含尽量多的高等级路段.以城市路网为例，当关键路段^j为快速路或主干路时，γ^j=1;当关键路段^j为次干路时，γ^j=0.5;当路段^j为支路时，γ^j=0.

z3为道路长度比，即关键路段集中应尽量包含较长的路段，其中L^j为第^j条关键路段的长度.

z4为配套设施比，即所选关键路段组中含配套设施的路段数量与总关键路段数量之比.当关键路段^j上有配套设施时，λ^j=1;否则λ^j=0.

1.4.2 多目标优化模型的简化求解

对于多目标优化问题，如果要求若干目标同时实现最优往往是很难的.目前有很多方法将较复杂的多目标问题转化为较容易求解的单目标或双目标问题，例如主要目标法、线性加权和法、分层序列法等.考虑到实际情况，将路径覆盖率最大作为主要目标函数，将其他目标函数转化成约束条件，从而将这个多目标函数转化成一个较为简单的单目标函数求解.具体目标函数描述如下:

通过模型的简化，可以将多目标优化问题转化为简单的线性单目标优化问题，并通过遗传算法、蚂蚁算法等进行求解.其中ε1、ε2、ε3的值根据实际路网情况确定.

1.5 由关键路段组流量推算全网流量

通过式(9)可以优化得到最佳关键路段组，下面以关键路段组流量为基础，分析推算其他路段流量的方法.假设路段流量矩阵为F1×n，路径流量矩阵为Pm×1，路径－路段发生矩阵为Lm×n，则

完备性 通过矩阵F1×n，任意非关键路段上的流量都可由关键路段上的流量推出.

证明 假设b=rank(Lm×n)，则路网中存在b条关键路段.为路径与关键路段的发生矩阵，为路径与非关键路段的发生矩阵，;则 Lm×n=［LILNI］.那么

在线性代数中，若α1，α2，…，αr线性无关，α1，α2，…，αr，β线性相关，则β可由α1，α2，…，αr线性表示，且表示法唯一［10］.由此定理可知，关键路段的发生矩阵LI中每个列向量都是线性无关的，因此非关键路段的发生矩阵LNI中的任一列向量都可由LI中的列向量线性表示，即

则任意非关键路段上的流量可表示为

唯一性 不同的关键路段组推出的全网流量是唯一的.

证明 假设选取不同的关键路段组布设检测器，则路径与非关键路段的发生矩阵分别为LNI1、LNI2，所对应的路段流量矩阵为F1、F2，根据式(10)可得

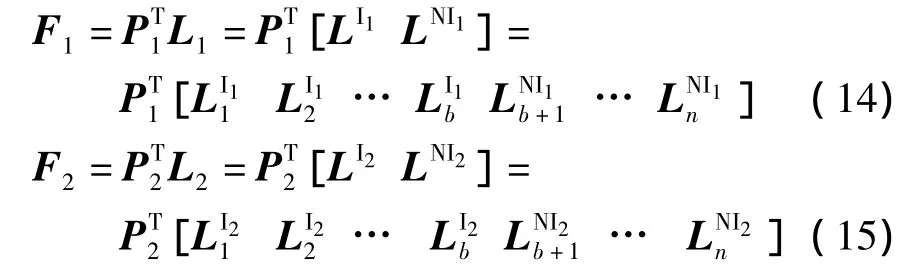
假设第1组的发生矩阵L1中的第i(i＜b)列与第j(b＜j＜n)列交换后组成了第2组的关系矩阵L2，由线性代数的定理可知，若α1，α2，…，αr线性无关，α1，α2，…，αr，β线性相关，则β可由α1，α2，…，αr线性表出，且表示法唯一［10］.故第一组中第j条路段的流量Fj可求出且表示唯一，即Fi=PTLI1，Fj=PTLNT1j;同理，交换后的第j条路段的流量F'j可求出且表示唯一，即由于第i条路段与第j条路段流量不变，故

对于LI和LNI中的所有列向量都可进行交换，因此不同的关键路段组推算出的全网流量是唯一的.

2 实例分析

下面以Nguyen-Dupuis网络为例，对提出的模型进行验证.Nguyen-Dupuis网络中节点数量s=13，路段数量n=19，OD对集合W={va－vc，va－vd，vb－vc，vb－vd}.各路段的道路等级及道路长度如图1所示，其中箭头表示路段车流方向，箭头上方的数字表示所对应的路段的长度.且每个路段都设有配套设施.

图1 Nguyen-Dupuis网络道路等级及路段长度分布图Fig.1 Link grades and lengths in Nguyen-Dupuis network

2.1 算法步骤

(1)初始化，输入Nguyen-Dupuis网络的拓扑结构及OD对的分布情况;

(2)用k最短路算法通过邻接关系矩阵A13×13选择OD对间最优的m条路径，组成优选路径集合R';

(3)生成路径－路段发生矩阵Lm×n，并确定关键路段的数量b及若干关键路段组;

(4)通过多目标优化函数确定最优关键路段组;

(5)由关键路段测得的流量推算全网流量.

2.2 Nguyen-Dupuis网络中关键路段的确定

在以上步骤中，用k最短路算法选择每个OD对间路径时，以出行费用最小为目标可选出m条优选路径.当k=3时，生成的路径－路段发生矩阵的秩为8;当k=4时，生成的发生矩阵的秩为10;当k=5时，生成的发生矩阵的秩为10.可以看出，当k=3时，所选路径无法覆盖整个网络，所以关键路段的数量较少;当k=4时，所选路径已可以覆盖整个网络，所以Nguyen-Dupuis网络中关键路段的数量b=10.根据路网实际情况，将ε1、ε2、ε3的值分别代入式(9)，并用Matlab编程对优化目标函数进行求解，其结果如表5所示.

表5 优化目标函数求解结果Table 5 Results of optimized objective function

2.3 Nguyen-Dupuis网络全网流量的推算过程

以方案二的关键路段组为例对Nguyen-Dupuis网络布设检测器，初始 OD量为{va－vc，va－vd，vb－vc，vb－vd}={40，80，60，20}.图2所示为关键路段分布及全网流量图，图中虚线代表布设检测器的路段，虚线上方的数字为检测器测得的关键路段流量.实线代表未布设检测器的路段，实线上方的数字为通过关键路段测得的流量及路段间流量的相关性推算出的非关键路段流量，括号内的数字为实际非关键路段的流量.从图2中可以看出，该方法可以有效地推算未布设检测器的流量，并具有很高的精度.

图2 Nguyen-Dupuis网络中的关键路段分布及全网流量图Fig.2 Key links and link flows in Nguyen-Dupuis network

3 结语

文中主要根据交通路网中路段间流量的线性相关性，提出了一种检测器优化布设方法，以获得全网流量.此方法无需OD流量、路径流量、先验矩阵等前提假设条件，也不需要过多考虑出行者的路径选择行为，模型较为简单，且在筛选关键路段组时考虑了路径覆盖率、道路等级、道路长度、配套设施4种影响因素，能有效运用于实际交通路网.文中还以Nguyen-Dupuis网络为例验证了方法的有效性.此方法不仅适用于小型网络，对于大型地图匹配网络同样适用.由于该方法基于路径－路段流量的相关性假设，主要适用于静态或稳定交通流状态下的检测器优化布设，对于动态变化情况下的检测器优化布设效果还有待进一步的研究.

［1］ 周晶，盛昭瀚，何建敏，等.交通检测点分布规则及其数学模型［J］.东南大学学报，1998，28(6):59-63. Zhou Jing，Sheng Zhao-han，He Jian-min，et al.Location rule and modeling of traffic counting points［J］.Journal of Southeast University，1998，28(6):59-63.

［2］ Yang Hai，Yang Chao，Gan Li-ping.Models and algorithms for the screen line-based trafflc-counting location problems［J］.Computers＆Operations Research，2006，33(3):836-858.

［3］ Mínguez R，Sánchez-Cambronero S，Castillo E，et al.Optimal trafflc plate scanning location for OD trip matrix and route estimation in road networks［J］.Transportation Research Part B:Methodological，2010，44(2):282-298.

［4］ Bianco Lucio，Confessor Giuseppe，Pierfrancesco Reverberi.A network based model for traffic sensor location with implications on O/D matrix estimates［J］.Transportation Science，2001，35(1):50-60.

［5］ 伍建国，王峰.城市道路交通数据采集系统检测器优化布设点研究［J］.公路交通科技，2004，21(2):88-98.Wu Jian-guo，Wang Feng.Study on optimal layout of traffic detector for traffic data collection system in urban area［J］.Journal of Highway and Transportation Research and Development，2004，21(2):88-98.

［6］ Castillo Enrique，Menéndez José María，Sánchez-Cambronero Santos.Predicting traffic flow using Bayesian networks［J］.Transportation Reasearch Part B:Methodological，2008，42(5):482-509.

［7］ Castillo Enrique，Menéndez José María，Sánchez-Cambronero Santos.Traffic estimation and optimal counting location without path enumeration using Bayesian networks［J］.Computer-Aided Civil and Infrastructure Enginee-ring，2008，23(3):189-207.

［8］ Hu Shou-Ren，Peeta Srinivas，Chu Chun-Hsiao.Identification of vehicle sensor locations for link-based network traffic applications［J］.Transportation Reasearch Part B: Methodological，2009，43(8/9):873-894.

［9］ 殷剑宏，吴开亚.图论及其算法［M］.合肥:中国科学技术大学出版社，2003.

［10］ 戴天时，陈殿友.线性代数［M］.北京:高等教育出版社，2004.