关于单形宽度的Sallee猜想的加强

潘娟娟 杨世国， 刘家保

(1.安徽大学数学科学学院，安徽合肥 230039;2.安徽新华学院数理部，安徽合肥 230038;3.合肥师范学院数学系，安徽合肥230061)

0 引 言

设K为n维欧氏空间En中的有界凸体，对En中的每个单位向量μ、凸体K的一对与μ垂直的支撑超平面之间的距离记为τ(K，μ)，令

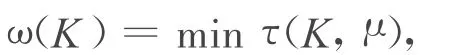
称ω(K)为凸体K的宽度[1]。

关于En中有界凸体宽度的研究是凸几何学中一个非常重要的课题。

Sallee于1974年对En中n维单形 Δn的宽度提出了内接已知超球面的所有单形中，正则单形具有最大的宽度[2]。

文献[1]证明了Sallee这一猜想，建立了n维单形Δn的ω(Δn)与外接球半径R之间成立的不等式，即

(1)式等号成立当且仅当 Δn为正则单形，其中

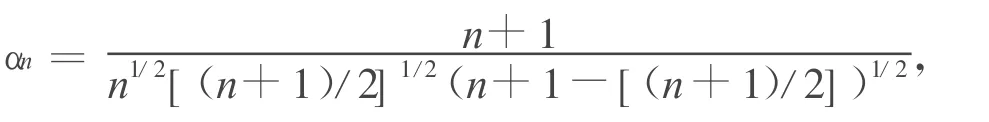
本文约定[m]表示实数m的最大整数部分。

文献[3]得到比Sallee-A lexander定理更强的结果，即在n维单形Δn的宽度ω(Δn)与体积V之间成立不等式，即

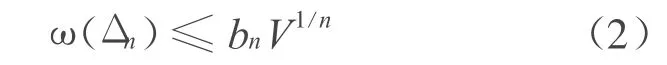
(2)式等号成立当且仅当 Δn为正则单形，其中

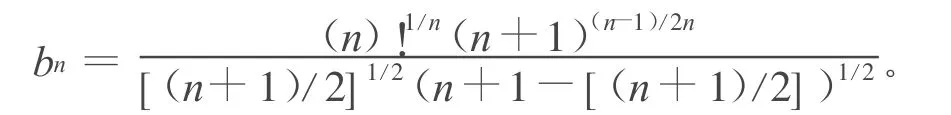
本文研究了单形宽度的类似问题，得到不等式(3)、(4)，加强了不等式(1)、(2)。

1 主要结果

设n维欧氏空间En中n维单形Δn的顶点集S={A1，A2，…，An+1}，体积为V，各侧面面积为Fi(i=1，2，…，n+1)，外接球半径为R，棱长为ρij=|Ai Aj|(1≤i＜j≤n+1)，τ(Δn，μ)表示单形Δn在方向μ的宽度，对n维单形Δn，记

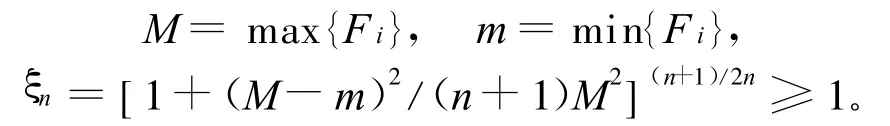
定理1 在n维单形Δn的宽度ω(Δn)与体积V之间有不等式，即

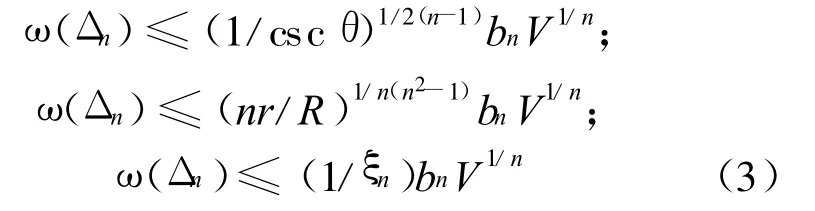
等号成立当且仅当Δn为正则单形。

定理2 在n维单形Δn的宽度ω(Δn)与外接球半径R之间有不等式，即

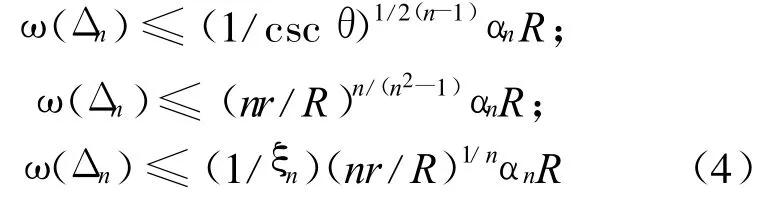
等号成立当且仅当Δn为正则单形。

由于cscθ≥1，R/nr≥1，ξn≥1，因此不等式(3)加强了不等式(2)，不等式(4)加强了不等式(1)。

2 引理和定理的证明

2.1 引理及证明

为了证明定理1、定理2，本文引用以下几个引理。

引理1 对En中n维单形Δn，有

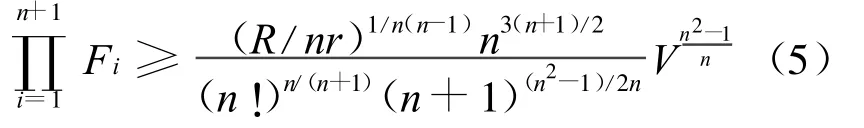
等号成立当且仅当Δn为正则单形[4]。

引理2 对En中n维单形Δn，有

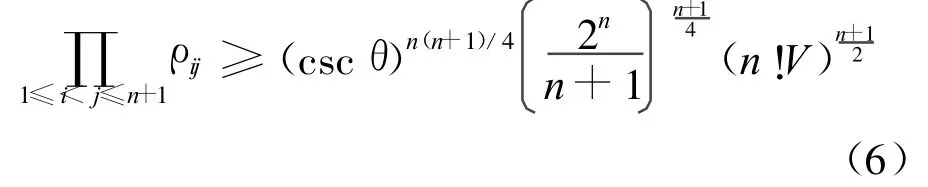
等号成立当且仅当Δn为正则单形[5]。

引理3 对En中n维单形Δn，有

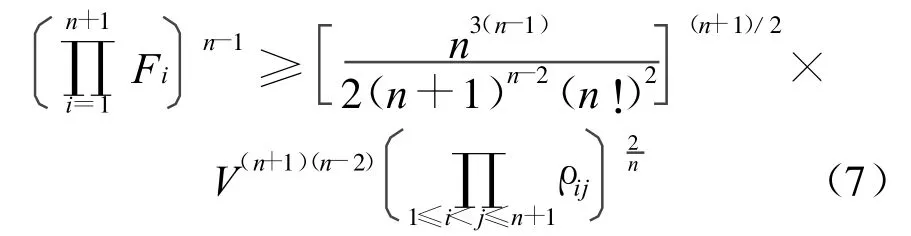
等号成立当且仅当Δn为正则单形[6]。

由引理2、引理3可知不等式(8)成立。

引理4 对En中n维单形Δn，有

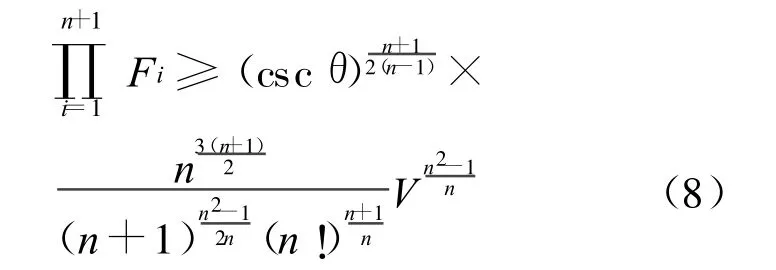
等号成立当且仅当Δn为正则单形。

引理5 设m个正数xi(i=1，2，…，m)的算术平均值为 Am(xi)，几何平均值为Gm(xi)，X=max{xi}，x=min{xi}，则

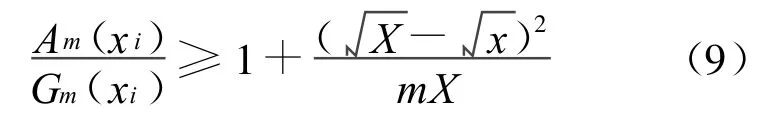
当x1=x2=…=xm时等号成立[7，8]。

引理6 对En中n维单形Δn，有

等号成立当且仅当Δn为正则单形。

证明 应用文献[9]中不等式，即

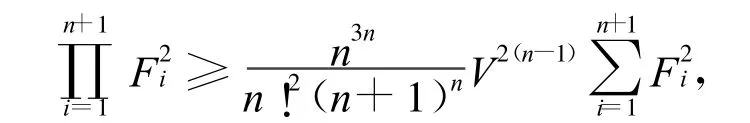
变换形式即得:

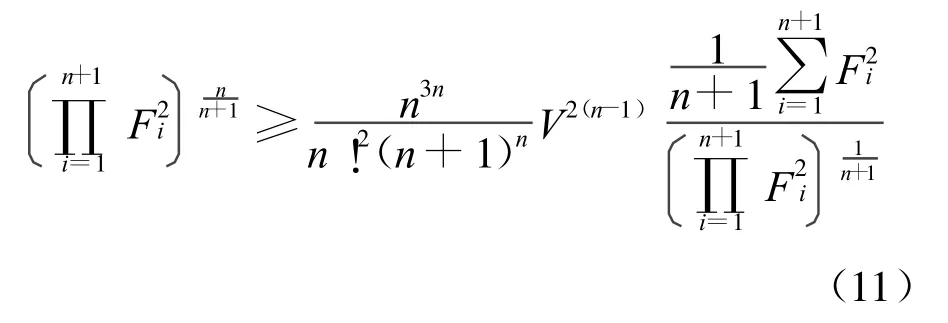
对不等式(11)右端应用引理5便得不等式(10)，易知不等式(10)中等号成立当且仅当Δn为正则单形。

引理7 对En中n维单形Δn，有

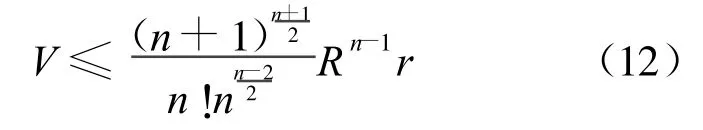
等号成立当且仅当Δn为正则单形。

证明 利用单形体积公式及幂平均不等式，有

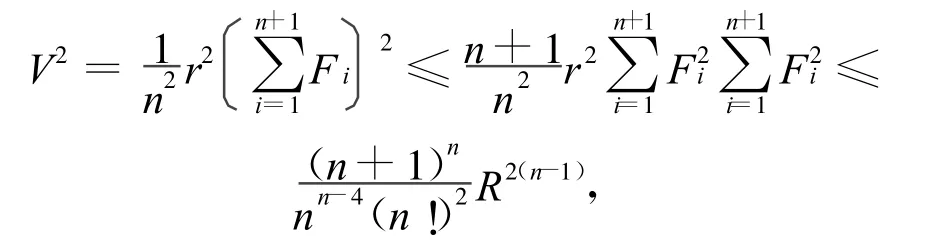
整理便得不等式(12)，易知等号成立当且仅当Δn为正则单形。

引理8 对点集S的每一个非空真子集A，En中必存在一定向超平面H，使SA⊂H，且A中的各点到H的带号距离都相等，若以v表示H的单位法向量，这个带号距离的绝对值为τ(Δn，v)[3]。

令I={1，2，…，n+1}，θm表示I的一切m元子集所成的集合，即

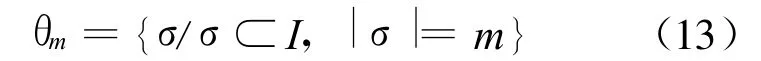
其中，|σ|表示集合σ的元素个数。于是单形 Δn的顶点集S的每个子集Sσ可以和I的一个子集σ对应，即

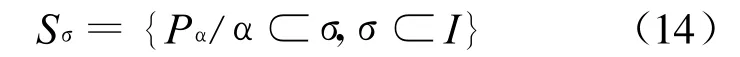
且当1≤|σ|≤n时，由引理8可知，存在定向超平面Hσ，使Sσ中一切点到Hσ的带号距离都相等，这个带号距离仅与Hσ有关。若以Vσ表示Hσ的单位法向量，当 Δn取定时，τ(Δn，Vσ)仅与σ有关，故可记:

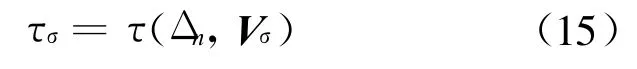
在上述记号之下，由文献[3]有引理9和引理10。

引理9 对En中n维单形Δn，有

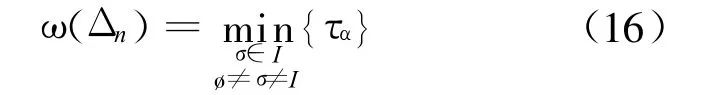
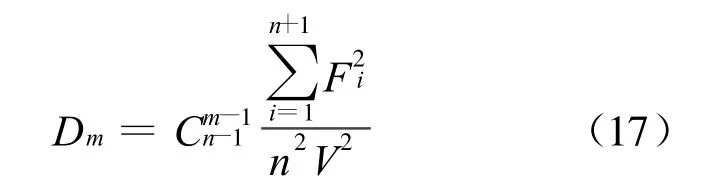
2.2 定理1的证明

证明 对一切σ∈θm，计算 τ-2α的算术平均AM(τ-2

α)，由引理9有:

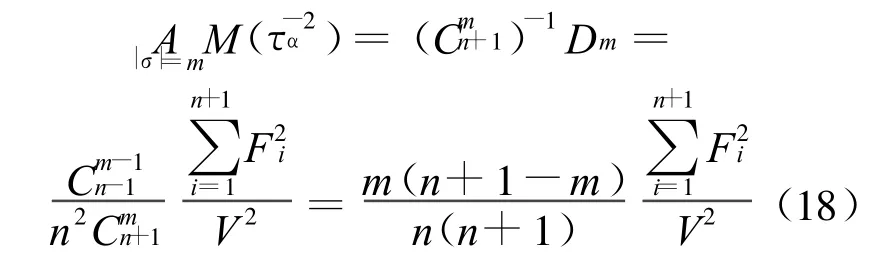
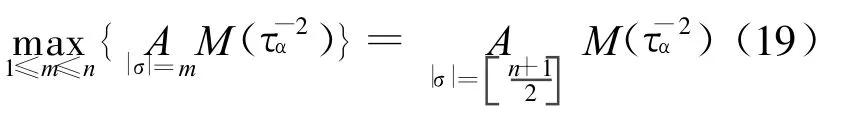
由引理8可知:

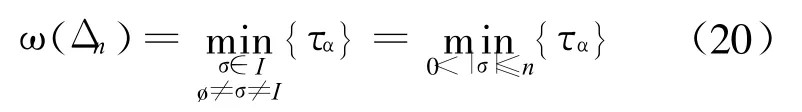
故

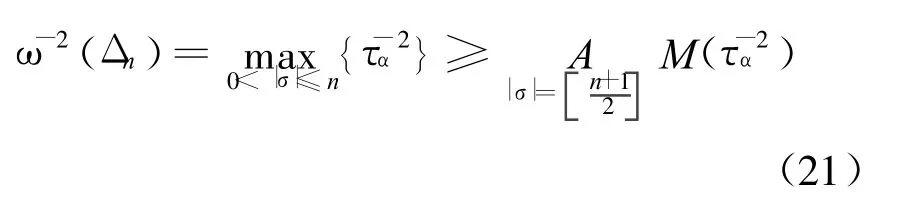
由(21)式与(18)式，可得:

将不等式(5)、(8)、(10)左端应用算术-几何不等式，便得:

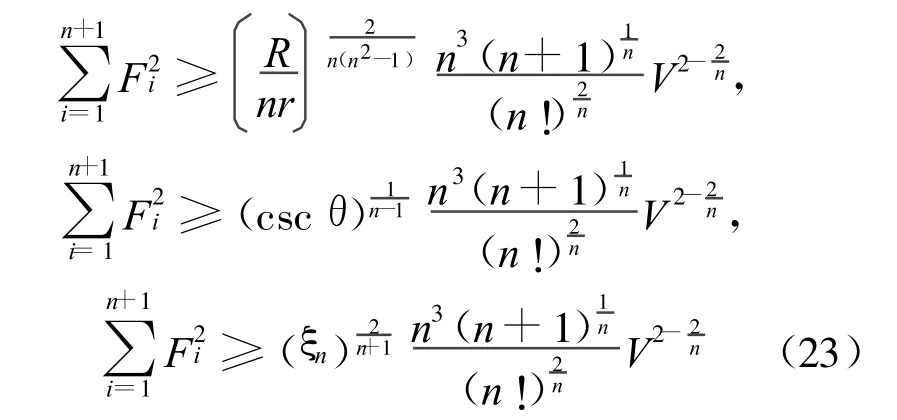
将不等式(23)代入不等式(22)化简便得不等式(3)，定理1得证。另将不等式(12)代入不等式(3)，化简便得证定理2。

[1] A lexander R.The w idth and diam eter of a simplex[J]. Geometriae Dedicata，1977，(6):87-94.

[2] Guy R K.The geometry of metric and linear space[M]. New York:Springer-Velag，1975:233-244.

[3] 杨 路，张景中.度量方程应用于 Sallee猜想[J].数学学报，1983，26(4):488-493.

[4] 沈文选.单形论导引[M].长沙:湖南师范大学出版社，2000:375-384.

[5] 冷岗松.En中Euler不等式的一个加强[J].数学的实践与认识，1995，(2):94-96.

[6] 苏化明.一个涉及单形体积棱长及侧面面积的不等式[J].数学杂志，1993，13(4):453-455.

[7] 杨世国.涉及两个n维单形的不等式[J].浙江大学学报:理学版，2006，33(3):247-249.

[8] 齐继兵，杨世国.关于垂足单形体积不等式的推广[J].合肥工业大学学报:自然科学版，2007，30(6):794-797.

[9] 张景中，杨 路.关于质点组的一类几何不等式[J].中国科学技术大学学报，1981，11(2):1-8.