关于电能可以倍增的探讨
能量守恒,众所周知。然而在用直流脉动电源对电容器脉动充电时出现的结果却令人意外,电能可以倍增。因我们水平,手段有限,给出的解释未必正确。然而若其不谬,相信可为能源建设作些贡献。
通常情况下直流恒压电源(1)经开关(2),电阻(3)对电容器(4)充电的线路如图1所示,其电源电压为U,充电平均电流为I,充电时间
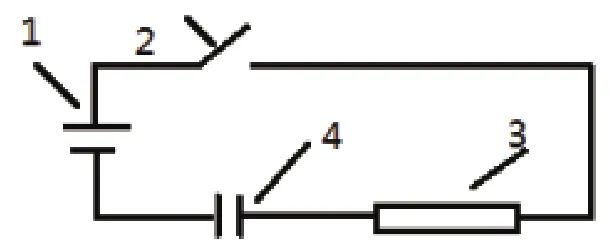
图1 直流恒压充电线路图Figure1 DC constant votage charge circuit
为T,电容器由0被充电到某一电压值为Uc。充电曲线如图2所示,充电电流,电压变化规律分别为:i=(U/R)*e∧(-t/RC),u=U-Ue∧(-t/RC),式中R为电阻,C为电容,t为时间。若该电源改用脉宽周期比(空度比)为1/N的脉动方式向同一电容器充电,脉冲宽度小于直流恒压充电过程所用时间的宽度,由于电容器的充电特性,其充电曲线如图3所示。此时充电平均电压为U/N,充电平均电流为I/N,充电时间为NT,电容器电压仍会由0被充电到同一电压值Uc。
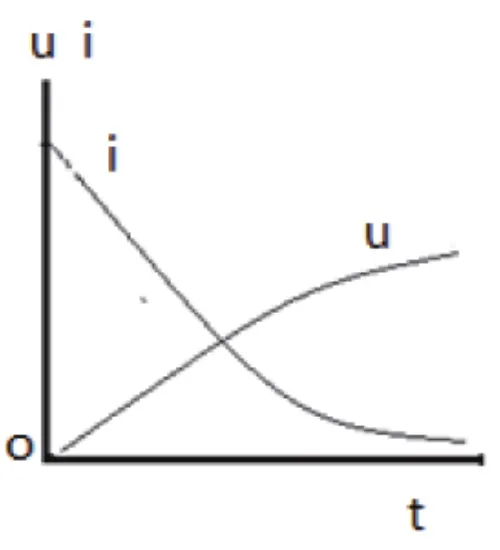
图2 直流恒压充电曲线Figure 2 Dc constant votage
由以上两图比较可知,图1中的连续充电曲线在图2中变为阶段的充电曲线。图2中的充电电流在无脉冲时降为零,电容器上的电压保持断电时的电压值;在有脉冲时,电压,电流曲线仍按原有规律进行变化。从以上两图可以看出,同一电容器由0被充电到相同电压值Uc时,不同的充电方式其输入电能也大不相同。
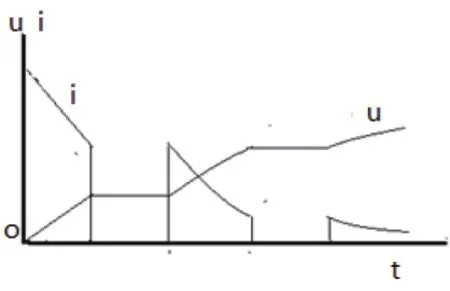
图3 直流脉动充电曲线Figure 3 DC pulse charge curve charge curve
图1中直流恒压充电的输入电能为U*I*T=UIT。
图2中直流脉动充电的输入电能为U/N*I/N*NT=UIT/N。
以上两式表明,同一电容器被充电到相同电压值时脉动充电的输入电能为恒压充电的输入电能的1/N。对于电压值为Uc的同一电容器来讲它对外输出的电能是一定的,而脉动充电的输入电能又是减小的。这就是说在脉动充电的情况下,电容器的输出电能最终会大于输入电能。以上讨论是不考虑各种电阻的理想情况。而在存有各种电阻的实际情况下,必然会增加部分能量的损耗。由于线路各种电阻基本为一固定值,所以只要脉宽周期比小于某一临界值,仍可实现输出电能大于输入电能的目的。为减小输入电能中电阻的能量损耗:减小充电电阻;电容器在电源电压的较高位置上运行以减小充电电流,这些都有利于提高输出与输入之比。我们分别用正弦工频全波,半波以及频率为60Hz,脉宽周期比为1/3的方波对6000μ的电容器进行充电实验,证明上述结论成立。数据如表1和表2。

表1 正弦全波,半波充电数据Table 1 Sine whole wave,half wave charge data
从上述列表可以看出,随着脉宽周期比的递减,电容器的输出电能与输入电能之比呈递增。当脉宽周期比降到某一临界值时,输出电能与输入电能之比会大于一。例如表2中当脉宽周期比为1/3时,二者之比大于一,电能实现了大于一的倍增。由于数据采集是普通万用表,故而数据不太精确,误差较大,但还是可以说明问题本质(也可以使用电能表直接测量电能值)。由此可以得出结论:直流脉动电源(可以是各种波形)对电容器脉动充电,当其脉宽周期比小于某一临界值且电容器在电源电压较高位置上运行时,电容器的输出电能可以大于输入电能,电能实现倍增。也就是说在电容器直流脉动充电的这一特定情况下能量是不守恒的。

表2 方波充电数据(脉宽周期比:1/3,频率:60赫兹)Table 2 Square wave charge data(pulse duration ratio:1/3,f:60Hz)
根据上述原理很容易做成电能倍增装置,可广泛用于工业,交通,野外,民用等多种场合。此装置多台,多级组合还可实现大功率,大倍率的电能倍增。以上是我们的浮浅看法,错误颇多,真诚欢迎批评指正。
[1]广东师范学院物理系.电工学(上册)[M].北京:人民教育出版社,1976:212-214.
[2]张瑞华,李士琨.电子线路分析基础(上册)[M].北京:电力工业出版社,1981:410-411.
[3]赵凯华,陈熙谋.电磁学(上册)[M].北京:人民教育出版社,1978:126-128.
[4]实用电工手册编写组.实用电工手册[M].北京:北京科学技术出版社,1983:552-553.
[5]黄正中.高等数学(上册)[M].北京:人民教育出版社,1978:232-237(第2版).

