地下水数值模拟过程中的误差分析

赵春虎,田 干,郭国强 ,何 渊

(煤炭科学研究总院西安研究院,陕西西安 710054)

地下水数值模拟是地下水研究中一项重要的应用技术,因其具有输入数据的兼容性好,计算过程的操作性强,输出结果的可视化程度高等特点,已广泛应用于水文地质,工程地质,环境地质等领域。地下水数值模拟主要是基于有限差分法与有限元法等数值技术,模型的种类有水流、水质的预报模型、地下水资源的管理模型;模型有三维流模型、二维流模型、确定性模型和随机性模型等。解决的问题包括地下水资源评价、地下水水位、地下水污染预测及地下水资源管理等。地下水数值计算是当前解决地下水资源预测与评价及地下水水质问题的强有力手段[1]。数值模拟作为一种定量研究地下水水量、水质的技术手段,模型的仿真程度是影响地下水研究的主要方面,所以分析和研究地下水建模过程中误差来源是提高模型仿真程度基础工作。无论是有限差分与有限元其离散化特点和建模、输入到输出过程中不可避免存在着误差,本文主要以当今世界范围内地下水研究中应用最广、较为成熟的地下水模拟软件(MODFLOW,FEFLOW等)为例,分析数值模型的误差来源及其一般提高模型仿真程度的数值处理技术。

1 水文地质概念模型

把具体物理模型的边界性质、内部结构、渗透性质、水力特征和补给排等条件抽象化为便于进行数学描述的概念模型,是数值模拟基础工作。客观资料的占有情况和地质与水文地质条件的主观认识程度决定了地下水系统的概念模型的合理化程度。因而必须充分收集模拟区地质与水文地质资料,采取必要水文地质补勘手段(钻探、物探、化探、试验等)进一步认识水文地质条件。由于含水系统介质各向异性等水文地质条件的时空差异,不可避免地进行条件的概化,例如模型分层、边界条件概化等。

2 数学模型

建立地下水流动的数学模型是数值仿真技术核心内容,主要有以水流连续性原理为基础的偏微分方程与以达西定律和水均衡原理为基础的水均衡方程分别构成其数学模型,均可以得到以微分为基础的微分方程(组)(式 1,以三维为例),其两种方法结果是相同的,但后者更直观,物理意义更明确,易于被人接受[2]。根据地下水流特征,一个由多个含水层组成的含水系统可相应概化为二维模型、准三维模型和三维模型[3],无疑三维数学模型更能反映地下水在三维空间中的流动与迁移特征(压力与物质的迁移)。所以针对同一问题选择不同(维数)的数学模型,其误差的原因与程度是显而易见,实际工作中针对问题特征和不同的精度要求及现场资料等情况来选择合适的数学模型是地下水数值仿真技术基础。

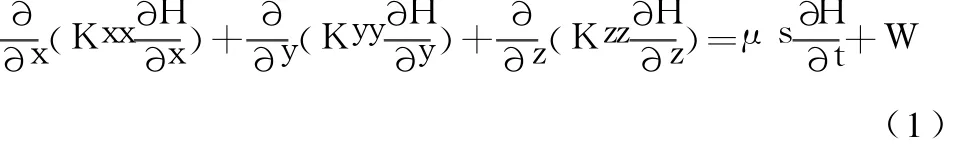
式中：x,y,z为笛卡尔坐标轴;t为时间;H为已知水头;Kxx,Kyy,Kzz,为坐标轴方向的主渗透系数;μs为比弹性给水度;W为单位体积井流量,抽水时取负号;

3 数值模型的构建

建立描述地下水流动的数学模型后有限差分格式采用的是差商代替微商做法,源于结构力学的有限元技术同样通过区域剖分和插值方法将描述地下水流的定解问题化为代数方程组求解,一般采用变分原理来形成系数矩阵迭代求解,形成数值模型。所以原来数学模型的解析解(精确解),转化为数值模型的近似解,存在着截断误差。这也是数值技术以离散化为基础形成误差的客观原因。

3.1 离散化网格的生成问题

对研究区域在空间上的离散,平面上主要有矩形(MODFLOW、GMS等)、三角形(FEFLOW、PGMS等)、任意多边形(陈崇希等)主要离散方式,其各具特点：矩形对重点区域如河流、断层、抽(注)井刻画较难,加密网格同时发生在行列之上,这样相对浪费结点数目,但计算格式与速度较好;三角形与任意多边形可对重点区域进行局部加密,刻画程度较高。层间一般按含水介质结构概化为多层,反映在网格的垂直剖分上,其概化的合理程度,层间的是否反映层面空间起伏状态均影响着模型的仿真程度。

3.2 模型的输入中的误差

模型输入中的误差来源主要是指基于数学模型的定解条件(包括边界条件,初始条件),及模型中各项水文地质参数的输入,井孔抽注、降雨、蒸发等源汇项数值处理上带来的误差。

3.2.1 定解条件的处理

边界条件是指模拟区边界上的水头分布和变化情况或者边界上流入(出)含水层的水量分布和变化情况已知的条件。其数学形式为：

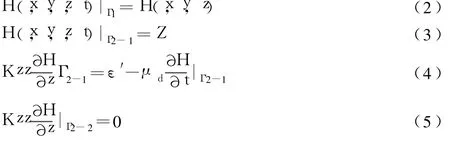
式中：H为已知水头;Kxx为坐标轴方向的主渗透系数;μd为重力给水度;Γ1为第一类边界;Γ2-1为潜水面边界;Γ2-2为零流量边界;ε′为降雨入渗补给量。

边界条件主要有两类：第一类边界条件(已知水头分布的边界)(式 2,3),该类边界条件主要技术问题在于概化的合理性,如定水头、一般水头边界在时间上定量分布的输入误差,在空间上河流垂向切割层位、水平切割含水层的河段等输入误差。第二类边界条件(已知边界上单位宽度流量变化规律)(式 4,5),此类边界条件在区域地下水模拟中尽量应用其零通量边界(隔水断层、地下水分水岭界面等自然边界),这样就可以极大的避免人为观测、概化的影响,但是由于地理、地貌、地质等条件的限制(如自然边界距离较远),往往必须选取非零量边界来刻画,这样在边界的流量输入的定量程度对水均衡计算有较大影响。另外在具体的研究问题中边界条件往往存在时空不稳定性,如河流边界水头季节性变化、地下水分水岭空间推移等问题。边界条件选择与刻画是影响地下水模拟仿真程度的最重要因素之一。

初始条件是指 t=0时渗流区D内各点(x,y,z)处的水头分布情况的条件。其数学形式为：

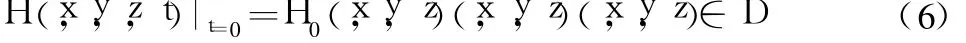
其中 H0为t=0时刻渗流区 D内各结点处水头值;

初始水头一般选取时段模拟区内水位观测井的统测水位再经过插值(如克里格)得到全区等水头值线作为模拟初期(t=0)初始水头条件。在对大区域非稳定流仿真过程中初始水头的可靠程度极大的影响了地下水资源量评价精度,稳定流仿真过程中初始水头的选取影响迭代运算速度与质量。另外在水位统测过程中混合观测井问题、动水位问题、目的含水层水头问题是影响水位统测质量主要因素。陈崇希教授在模型应用中采用“参数迭代法”来确定水头未知的含水层的初始水头提高了其合理性。

3.2.2 水文地质参数、源汇项的输入

通过野外抽水试验、实验室测试所得的水文地质参数或经验结构参数,这一系列参数是正演模型模拟计算及预测的基础,极大的影响管理模型、预测模型的仿真程度。在模型识别校正阶段一般通过实测和计算曲线的拟合程度来调整水文地质结构参数(通常限定一定的取值范围),进一步提高模型的仿真程度。但水头变化是地下水压力传递(相对于溶质运移的物质传递)的结果,所以其拟合标准存在一定的片面性。在模型校正过程中应用示踪剂示踪(如 MODPATH),水质模型的浓度模拟(MT3D)与实测校正等手段来综合识别各项参数的合理性是更加可靠的。

源汇项(如降雨,蒸发,开采等)其主要问题表现在输入数据观测统计质量与处理技术：开采井含水层的开采层位确定,混合开采井的各含水层的流量分配,MODFLOW中主要根据导水系数确定各层的流量分配,黎明博士对此处理技术提出了质疑[4],实际过程中要复杂的多。大区域开采总量的统计与分配,一般采用面状分配,而不是以实际抽水井为源汇来处理的。降雨与蒸发等同样存在处理的合理性问题,MODFLOW中降雨只发生在第一层且为瞬时补给地下水,一般实际过程中地下水对降雨的响应表现出较明显的滞后效应。蒸发的处理是通过设置一经验临界深度,以此设定埋深大于此深度其蒸发量为零,这样的数值处理方式明显存在偏废。陈崇希教授提出在处理混合井流和混合观测孔时,采用了“渗流 -管流耦合模型”;在处理河流入渗和降雨入渗方面采用了“入渗滞后补给法”;处理潜水蒸发方面,采用了非线性关系来刻画潜水蒸发强度和潜水位埋深的关系,较高程度的提高了模型的仿真程度。

3.2.3 其它输入

在我国北方地区河流是补给地下水的主要来源之一,类似于作为第一类自然边界条件的河流其时空变化规律(如水位在时间上的变化,在空间上河流垂向切割层位、水平切割含水层的河段位置),在模拟区内对河流的合理处理是相当重要的。泉作为地下水在地表排泄点存在一定的技术处理难度。另外,小溪、水平挡墙、排水沟等水文地质要素同样存在概化的合理性问题。

4 模型的运行与输出

模型运行主要体现在对方程组求解方法的选择上,以有限差分为基础的 MODFLOW其求解方法主要有：强隐式法(Strong Implic it Procedure,SIP),逐次超松弛迭代法(Successive Over Relaxation,SOR),预调共轭梯度法迭代法(Preconditioned Conjugate Gradient,PCG)[5],后者较前两者有占内存小,运行速度快等优点,故多采用此法,但前者更适合于解决非线性问题。另外迭代次数的限制、收敛标准的设定等运行参数,对模型的计算结果必然存在影响。

5 结论

地下水数值仿真一般过程：以实地的物理模型为基础经分析概化形成合理的概念模型,选择合适的数学模型来描述地下水流场特征,在空间和时间进行离散化(稳定流时间上不需要离散)形成以结点为基础的数值模型,最后进行模型的运算与输出。

从地下水系统的物理模型概化成合理的概念模型主要依靠于实地资料详实程度与建模者的认识程度与专业基础;选择合适的数学模型取决于研究精度与软件自身的限制;形成数值模型影响因素则较多,主要体现在模型在时空上的离散化尺度,以及各种条件输入状态(定解条件、参数及源汇项等);模型运行可根据问题特点选择不同求解方法和设定合适的运行参数。陈崇希教授提出“防止模拟失真,提高仿真性是数值模拟的核心”[6],随着计算机硬件水平与地下水数值仿真技术的发展,地下水模拟的仿真程度将进一步提高。

[1]薛禹群,吴吉春.地下水数值模拟在我国——回顾与展望[J].水文地质工程地质,1997,24(4)：21-24.

[2]薛禹群.地下水动力学[M].北京：地质出版社,1997.

[3]叶淑君,戴水汉 地下水流二维、准三维及三维模型模拟结果比较[J]水文地质工程地质,2003(5)：23-27.

[4]黎明,刘文波,陈崇希.MODFLOW能模拟地下水混合井流吗?[J].水文地质工程地质,2003,(5)：116-117.

[5]马驰.SIP和 PCG2两种迭代法在地下水数值计算中的应用对比[J],西安科技学院学报 2002,22(1)：59-62.

[6]陈崇希.“防止模拟失真,提高仿真性”是数值模拟的核心[J].水文地质工程地质,2003,(2)：1-5.

[7]Carma San Juan Kenneth E.Kolm Conceptualization,characterization and numericalmodeling of the Jackson Hole alluvialaquifer using ARC/INFO and MODFLOW Engineering Geology 42(1996)119-137.