光纤陀螺光纤环Shupe误差的多参数影响仿真分析

宋凝芳 关月明 贾 明

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

光纤陀螺光纤环Shupe误差的多参数影响仿真分析

宋凝芳 关月明 贾 明

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

在光纤陀螺Shupe误差数学离散公式的基础上，建立四极对称法绕制光纤环的有限元模型，分析多材料组成下的光纤环在仿真时所需的综合物性参数.结合光纤陀螺工作环境的载荷和边界条件，对某型光纤环进行数值仿真，定量分析了光纤陀螺在工作温度下光纤环的Shupe误差，验证了模型建立的正确性.在此条件下，分析光纤环的结构参数、热学参数和热扰动参数对Shupe误差的影响.结果表明:通过增加绕制层数，提高导热系数，合理布置热源，可以明显抑制光纤环的Shupe误差，从而提高光纤陀螺的温度性能.

Shupe效应;光纤陀螺;有限元法;光纤环

光纤陀螺具有抗电磁干扰、动态范围大、可靠性高等优点，被广泛应用于空、天、海、陆领域中［1］.然而，作为核心部件的光纤环却对温度有着极高的敏感性，其周围温度场的不均匀变化引起的非互易性相移会使光纤陀螺的零偏产生漂移，称为Shupe效应［2］，这种非互易误差限制了光纤陀螺性能进一步提高.

鉴于此，研究人员对光纤环的Shupe误差机理进行了广泛研究.采用四极对称绕法将使Shupe误差减小3 个数量级［3］.文献［4］建立了光纤环温度漂移模型，得出减少光纤长度、增加绕制层数，热源位于环中间并且热流向外传播时，Shupe误差相对较小的结论.文献［5］基于有限元法，对光纤环中的温度场进行了较为精确的分析，认为通过优化光纤环、骨架结构及壳体的热传导性能，可以有效降低温度的影响.以上文献从不同角度明确了Shupe误差的影响因素，但均未深入讨论各因素对Shupe误差的影响程度.文献［6］建立了光纤陀螺系统三维热学模型.文献［7］建立了三维有限元模型分析光纤环Shupe效应.三维模型数据量大，能够准确反映模型内部情况，但计算量大.

本文在文献［5－6］的基础上，针对四极对称方法绕制的光纤环进行多参数影响的分析，研究光纤环内部影响因素:包括绕制层数、导热系数、密度、热容和外部环境中的热扰动等参数对光纤环Shupe误差的影响，并给出各参数的影响曲线.

1 理论基础

当光纤环中出现瞬间热扰动时，将引起沿光纤环的两束反向传播光波经历不同的相移，这种由温度引起的非互易性相移和由旋转引起的Sagnac相移无法区分，将在光纤陀螺中产生偏置误差.

光纤陀螺工作时，瞬间热扰动引起的旋转角速率误差 ΩE(t)［4］为

其中，D为光纤环有效直径(光纤环内外径均值);L为光纤长度;n为光纤有效折射率;∂n/∂θ为温度系数;为 z点 t时刻的温变速率;(L－2z)为位置相关权因子.由式(1)可知，ΩE(t)与微段光纤上的和(L－2z)的积分项成正比关系.

2 有限元模型

2.1 光纤环截面离散化

为了定量计算ΩE(t)，需要对光纤环进行离散化处理.高H，宽W，光纤外径为d，有效直径为D的标准光纤环和方向定义如图1所示.考虑到轴对称结构，将采用四极对称方法绕制的光纤环的三维模型简化为二维模型.将长度为L的光纤离散为N层，每层M匝，共MN圈光纤段，由此得到ΩE(t)的数值表达式为

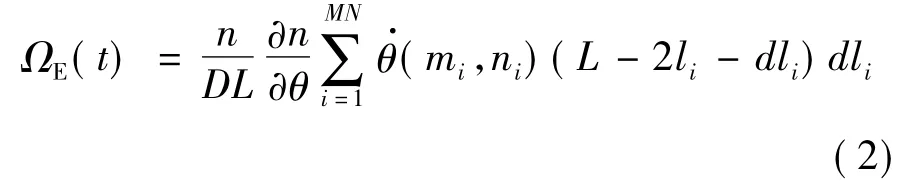
其中，MN为光纤绕制总圈数;li为第i圈光纤起始点的坐标长度;dli为第i圈光纤绕制长度;(mi，ni)为第 i圈光纤在模型中的坐标值;ni)为光纤环截面模型中第i圈光纤处的温变速率.

以某型号中精度光纤陀螺的脱骨架光纤环为例，几何参数为:H=10 mm，W=7.7 mm，D=91.5mm，N=48，M=60，d=165μm.采用四极对称方法，每圈在环中的位置如图2所示.

图1 光纤环示意图

图2 四极对称绕法模型

考虑到胶粘剂厚度的影响，涂胶后的光纤等效外径d’=170μm.根据每圈光纤在模型中的坐标，计算对应的li和dli，从而描述离散后每圈光纤的特征，L=lMN+dlMN，以此计算(L－2lidli)dli，如表1所示.

表1 绕环参数

2.2 网格的划分

采用ANSYS二维热单元Quad 4node 55进行计算.通过控制模型边界线划分单元数对光纤环截面二维模型进行网格划分，网格密度以保证每个光纤截面中心附近有一个节点为准.

2.3参数分析与计算

基于有限元法仿真时，通常将光纤环视为一个整体:以体积百分比得到多材料组成下的光纤环的密度ρ，导热系数λ的平均值，以质量百分比得到热容c的平均值.由前面参数可知，采用双涂覆层的保偏光纤，应用四极对称方法绕制光纤环，总体积为 2.21 ×10－5m3.光纤包层的外径为80μm，体积为 4.16 × 10－6m3，占总体积的18.8%.同法计算光纤内、外涂覆层体积比.光纤环中剩余体积，即光纤之间的空隙由成分为UV丙烯酸酯的胶粘剂填充.根据各组成的体积比和密度，计算出相应的质量比.

表2列出了光纤环中的各组成材料的物性参数:外径 Φ，ρ，λ，c，所占体积比 V 和质量比 M，由此计算得到光纤环的综合物性参数.

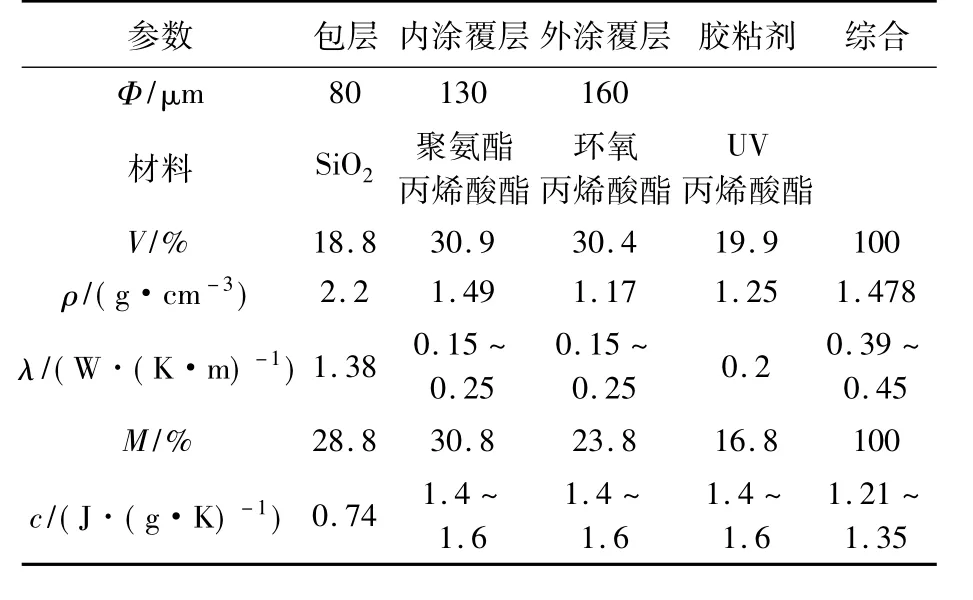
表2 光纤环材料的物性参数

3 模型验证

针对前面建立的光纤环模型进行有限元仿真，并定量计算Shupe误差.参考表1和表2的计算数据，光纤环的参数分别为L=827.873m，ρ=1.478 g/cm3，λ =0.42W/(K·m)，c=1.28 J/(g·K).为了确定光纤环模型的正确性，同时对该型号光纤环进行温度实验.

3.1 载荷与边界条件

温度实验时，光纤环由细线悬置于温箱中部，温箱内部空气与光纤环外表面进行自然对流换热.设定实验温度为:初始温度25℃，实验开始后以1℃/min的温变速率降温至－40℃，保温1 h，再以 1℃/min的温变速率升温至 60℃，保温55min，实验结束.总时间280min(16800 s).

在有限元仿真中，为了模拟温箱内传热情况，令空气与光纤环表面的自然对流换热为温度载荷，加载在光纤环的顶面、底面、内侧和外侧，取表面传热系数 h=5 W/(K·m2).仿真时间步长60 s.

3.2 结果对比

按照上述条件和方法进行有限元仿真和温度实验，温度曲线如图3所示.实测光纤环表面温度略微滞后于设定温度.由于热传递时间特性，仿真得到光纤环中心温度变化更加平缓.

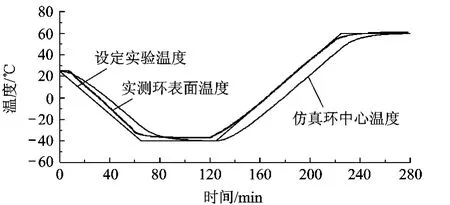
图3 温度曲线

温度实验与有限元仿真结果如图4所示.实测光纤环外壁的降温速率极值为1.3℃/min，升温速率极值为1.1℃/min;对陀螺输出数据进行10 s平滑处理，零偏极值为 1.37(°)/h，该曲线与温变速率曲线吻合.在本文设计的参数条件下，通过有限元仿真得到Shupe误差零偏极值为0.995(°)/h，Shupe 误差曲线与实测陀螺输出曲线一致.

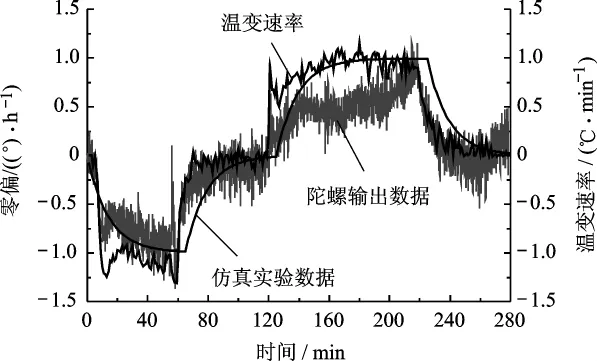
图4 实验与仿真结果

在光纤环的Shupe误差计算模型中，有限元模型建立合理，体积比法和质量比法参数计算准确，载荷和边界条件正确，则仿真方法准确可信.将该模型用于其他型号、尺寸光纤环的仿真，对比温度实验中陀螺输出数据，仿真曲线与实验曲线吻合较好，数量级相同，验证了光纤环模型建立的正确性.因此，以该模型分析光纤环的Shupe误差特性是可行的.

4 多参数影响分析

Shupe误差的大小受光纤环的结构参数、热学参数和外界热扰动参数的影响.结构参数主要包括N，M，D和L;热学参数主要包括λ，c和ρ;热扰动参数包括外界温度载荷的温变速率、扰动方向等.

4.1 结构参数的影响

结构参数一方面影响(L－2li－dli)dli的计算值，同时也影响光纤环中的温度分布.

由式(2)可知，ΩE(t)与D和L的乘积成反比.而当D和L同时固定时，光纤环的几何形状由层数与匝数比N/M控制.令ξ=N/M，当DL≈75.7m2，分别取 D=81.3mm，D=91.5mm 和 D=102.3mm时，光纤环的Shupe误差受结构参数ξ的影响，如图5所示.D一定时，光纤环的Shupe误差随ξ增加呈近似对数关系减小.这表明增大N可以明显抑制Shupe误差，但当N过大即ξ＞3时，Shupe误差受N增大的抑制程度减小且趋于定值.当DL一定时，热致误差的ξ影响曲线随D的增大(L的减小)而减小.

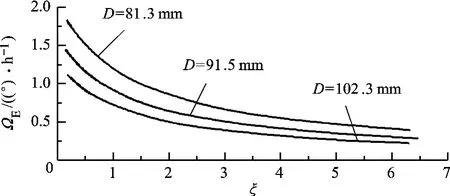
图5 Shupe误差受结构参数的影响

4.2 热学参数的影响

当载荷和边界条件确定时，热学参数直接影响热量在光纤环内部的传递速度，即光纤环中的温变速率 θ·(z，t).

根据选定的实验参数和条件，分别研究ρ，c和λ对Shupe误差的影响程度.图6为单独变化ρ，c和λ时的Shupe误差仿真结果，其中ρ的变化范围为1.2 ～2.0 g/cm3，c的变化范围为 1.2 ～2.0 J/(g·K)，λ 的变化范围为 0.2 ～ 1.2 W/(K·m).可以看出，Shupe误差随c和ρ增大而线性增大，随λ增大呈近似对数关系减小.其中ρ影响曲线斜率为0.645(°)·cm3/(h·g)，c影响曲线斜率为 0.69(°)·g·K/(h·J).

图6 Shupe误差受热学参数的影响

实际工程应用中，通过改变胶粘剂的成分从而改变光纤环的综合热学参数.在光纤环的胶粘剂中添加λ高的金属粉末来增加环的综合导热系数，可以有效提高光纤环的温度特性［8］.对于胶粘剂中掺杂银粉的光纤环进行仿真分析，已知纯银的物性参数为:ρ=10.5 g/cm3，c=0.23 J/(g·K)，λ =427W/(K·m)，当银粉掺杂比例为胶粘剂体积的0.1%时，光纤环的综合物性参数为:ρ=1.48 g/cm3，c=1.30 J/(g·K)，λ =0.51W/(K·m);掺杂比例为1%时，光纤环的综合物性参数为:ρ=1.50 g/cm3，c=1.29 J/(g·K)，λ =1.27W/(K·m).可知，掺杂银粉对于光纤环的综合导热系数改变较大，由此引起的Shupe误差变化为1(°)/h量级，而对于综合密度和热容的改变很小，引起的Shupe误差变化为10－3～10－2(°)/h.因此通过添加金属粉末改变胶粘剂成分时，λ对Shupe误差的影响占主要地位，同时引起的综合热容和密度的变化可以忽略.

4.3 热扰动参数的影响

光纤环模型中，外界热扰动以温度载荷形式加载在光纤环的外表面，中点两侧等距的光纤段处于近似温度场.通过有限元仿真，研究热扰动的温变速率和温度载荷加载数目、方向对Shupe误差的影响.

由图4可知，温度实验中，实测降温速率大于升温速率，陀螺输出Shupe误差曲线的负向零偏绝对值大于正向零偏.有限元仿真的升温速率和降温速率均为1℃/min，Shupe误差曲线负向零偏极值等于正向零偏极值.该结果验证了式(2)中光纤环的Shupe误差与外界温度载荷的温变速率成正比的结论.

研究温度载荷对Shupe误差影响时，定义加载温度载荷的温变速率为1℃/min，换热系数为5W/(K·m2)，设定实验温度曲线如图3所示.

分别在光纤环的4个面加载温度载荷，仿真的Shupe误差曲线如图7所示.可以看出，外侧热扰动引起的误差最大，内侧热扰动引起的误差则最小.

同时在光纤环的任意两个面加载温度载荷，得到的Shupe误差曲线如图8所示.其中沿径向对称热扰动(内侧和外侧热扰动)引起的误差约是沿轴向对称热扰动(顶面和底面热扰动)的4倍.当热扰动不对称分布时，含外侧热扰动的温度载荷组合引起的误差较大.

同时在光纤环的任意3个面加载温度载荷，Shupe误差曲线如图9所示，不含外侧热扰动的温度载荷组合引起的误差最小.

图7 单方向热扰动对Shupe误差的影响

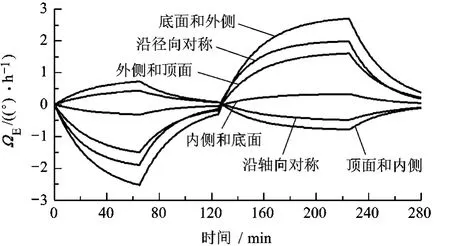
图8 两方向热扰动对Shupe误差的影响

图9 3方向热扰动对Shupe误差的影响

5 结论

本文利用有限元法对某型光纤环Shupe误差进行了定量分析，结合实验结果，验证了光纤环模型的正确性.利用该模型对光纤环的Shupe误差进行了多参数影响的分析，得出结论:增加光纤环绕制层数，增大光纤环综合导热系数可以明显减小Shupe误差;使热扰动方向沿轴向对称，避免热扰动由光纤环外侧向内侧方向传播，将有利于抑制Shupe误差.这对光纤环的参数设计和光纤陀螺内部的器件布局有一定的指导意义.

References)

［1］ Yin S，Ruffin P B，Yu F T S.Fiber optic sensors［M］.2nd ed.Boca Raton:CRC Press，2008:334 －335

［2］ Shupe D M.Thermally induced nonreciprocity in the fiber-optic interferometer［J］.Applied Optics，1980，19(5):654 －655

［3］ Frigo N J.Compensation of linear sources of non-reciprocity in Sagnac interferometers［C］//Moore E L.Fiber Optic and Laser Sensors:Proc of Technical Symp East.Arlington:Society of Photo Optical，1983:268 － 271

［4］ Mohr F.Thermooptically induced bias drift in fiber optical Sagnac interferometers［J］.Journal of Lightwave Technology，1996，14(1):27 －41

［5］ Tirat O F J，Euverte JFM.Finite element model of thermal transient effect in fiber optic gyro［C］//Udd E.Fiber Optic Gyros:20th Anniversary Conference.Denver:SPIE-International Society for Optical Engine，1996:230 －238

［6］ 孟照魁，崔佳涛，杜新政，等.光纤陀螺系统热建模及仿真［J］.北京航空航天大学学报，2007，33(6):701 －704 Meng Zhaokui，Cui Jiatao，Du Xinzheng，et al.Building model and simulation aboutheat of fiber optical gyroscope［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33(6):701－704(in Chinese)

［7］李茂春，刘铁根，王佳佳，等.光纤陀螺光纤环Shupe效应的三维有限元模型［J］.天津大学学报，2008，41(5):601－606 Li Maochun，Liu Tiegen，Wang Jiajia，et al.Three-dimensional finite element model of Shupe effect in FOG fiber coil［J］.Journal of Tianjin University，2008，41(5):601 －606(in Chinese)

［8］ Carlson K R，Cordova A，Rahn JP.Potting compound for fabrication of fiber optic gyro sensor coil and method for fabrication sensor:USA，6054068［P］.2000 －04 －25

(编 辑:刘登敏)

Analysis of multi-parameters effect on Shupe error in fiber optic gyroscope fiber coil

Song Ningfang Guan Yueming Jia Ming

(School of Instrument Science and Opto-electronics Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

The element model of the fiber coil with the quadrupole(QAD)winding pattern was built based on the discrete mathematics for mulae of the Shupe error in the fiber optic gyroscope(FOG)，and the comprehensive physical parameters of the fiber coil with multi-material composition were analyzed for the next simulation.Combining of the thermal loads and boundary conditions in the FOG working environment，the numerical simulation of the fiber coil was done to analyze the Shupe error in the fiber coil at the FOG operating temperature quantitatively.It also verified the correctness of the model building comparing with the experimental results.On this condition，the effects of structural parameters，thermal parameters and temperature disturbed parameters on Shupe error in the fiber coil were analyzed.The results show that by optimizing the winding layers，increasing thermal conductivity，and arranging heat source rationally，the Shupe error of fiber coils can be inhibited，thereby enhancing the FOG thermal performance.

Shupe effect;fiber optic gyroscope;finite element method;fiber coil

V 241.533

A

1001-5965(2011)05-0569-05

2010-03-03

宋凝芳(1968 －)，女，天津人，教授，songnf@263.net.