蚁群PID神经元网络在电厂球磨机控制中的应用

沈继忱，彭猛，宋刚

(东北电力大学自动化工程学院，吉林吉林132012)

0 引言

钢球磨制粉系统是一典型的具有非线性、大滞后系统，各控制量和被控制量之间存在着相当严重的耦合关系。以往的控制系统采用3套相互独立的PID控制回路，将它们之间的相互关系强行割裂，造成顾此失彼，各调节量之间难以优化匹配，以致制粉系统在低负荷下运行，耗电量很大［1-2］。对此，为了解决这些问题，本文提出了基于蚁群算法的PID神经元网络控制系统。

1 球磨机制粉系统数学模型

球磨机制粉系统输入变量分别是给煤量、热风量和再循环风量，输出变量分别是球磨机出口温度、球磨机入口负压和球磨机负荷，根据300 MW机组配备的球磨机的阶跃扰动曲线，取得球磨机制粉

系统的对象特性传递函数矩阵为:

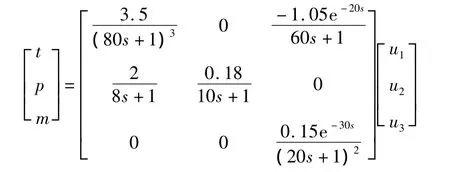
式中，t代表球磨机出口温度;p代表球磨机入口负压;m代表球磨机的负荷;u1、u2、u3分别代表热风门开度、再循环风门开度及给煤量，%。

2 基于蚁群算法的PID神经元网络控制系统

2.1 控制系统结构

PID神经元网络控制器是融入PID控制规律的多层前向神经网络控制器。它融合了常规PID控制器的优点，又具有神经网络的学习记忆功能和逼近任意函数的能力;并且具有在线学习的功能，隐含层分别定义了比例元、积分元、微分元;通过调整网络中比例元、积分元和微分元作用的强弱，使被控系统具有较好的静动态特性，能够很好地实现系统的控制［3］。根据上述球磨机制粉系统的数学模型，建立了PID神经元网络球磨机制粉控制系统结构，如图1所示。

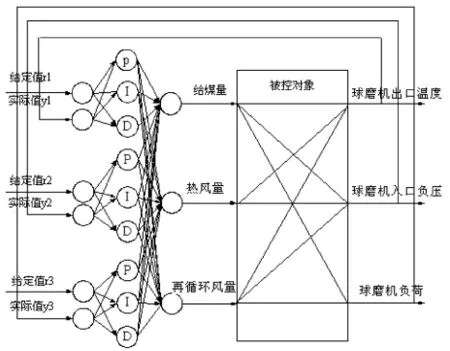
图1 PID神经元网络控制系统结构图

2.2 控制系统的算法

蚁群算法(Ant Colony Algorithm)是一种新型的随机搜索仿生类算法，1991年由意大利学者M. Dorigo［4］等人首先提出的。他们通过对蚂蚁觅食行为的研究，发现蚂蚁在其来往路径上留下一种称为信息素(Pheromone)的挥发性化学物质，整个蚁群的通信和协调就是通过信息素完成的，从而可以使多个路径上的蚂蚁经过相互协作都逐渐聚集到最短的那条路径上［5］。

PID神经元网络和大多数神经网络一样采用BP学习算法，由于BP学习算法采用的是局部区域沿梯度下降算法，通常收敛的时间很长，而且不可避免地会陷入局部极值。而蚁群算法适合全局优化搜索，容易得到全局最优解。所以，蚁群算法和PID神经元网络结合起来组建系统，可兼有PID神经元网络的广泛映射能力和蚁群算法的快速、全局收敛以及启发式学习等特点，在某种程度上避免了PID神经元网络收敛速度慢，易于陷入局部极小点的问题，提高了控制系统的自学习能力。

基于蚁群算法的PID神经元网络控制系统的基本思想为:首先利用蚁群算法的全局寻优能力找到一组较优的初始权值组合，再利用BP算法进一步“细调”权值，找到真正的全局最优点。假定网络中需要优化的权值和阈值总数为s个，先将这些参数依次排序，记为p1、p2、pS，将每个参数设置一个集合Ipi，集合内为N个随机非零值，设定合适数量的蚂蚁，每只蚂蚁从第一个集合出发依次走到最后一个集合，在每个集合中依据各元素的信息素的值，按照概率公式选择一个元素，同时调节所选相应元素的信息素的值，当蚂蚁走完s个集合，也就是选择了一组网络权值。经过蚂蚁的不断迭代，最终找到最优解。

蚁群算法训练 PID神经元网络的实现步骤如下:

a.参数初始化。循环次数NC=0，定义最大循环次数NCmax，将M只蚂蚁都置于蚁巢，令集合Ipi(1≤i≤s)内的每一个元素信息量τj(Ip)(t)=C，(1≤j≤N(C为常数)，初始时刻△τij(0)=0。

b.这个步骤重复s次，直到蚂蚁走过所有集合。

令s=0

Set s=s+1

For k=1 to M do

每只蚂蚁从第一个集合出发依次在每个集合中按照概率式选择一个元素，对任一只蚂蚁k(k= 1，2，…，M)，在集合j中根据下式选择第j个元素。

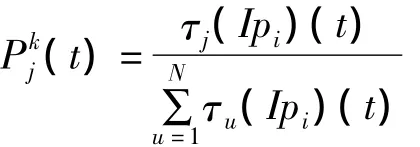
c.当蚂蚁走完s个集合，该过程经历了s个时间单位，对所选元素的信息素按下式做相应调整。τj(Ipi)(t+s)=ρτj(Ipi)(t)+Δτj(Ipi)，其中ρ为信息素轨迹的残留因子。

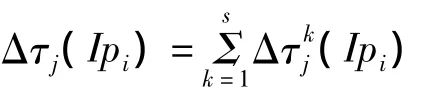
式中，Q是常数，表示完成一次循环后蚂蚁所释放的信息素总量;ek为蚂蚁k在本次循环中选择的元素作为神经网络的权值时得出的实际输出与期望输出之间的误差。记录最小误差对应的权值。

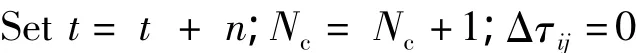
d.If Nc＜NcmaxAND所有的蚂蚁没有选择同一组权值

Then转到(2)

否则，输出最好权值，算法结束。

3 仿真结果

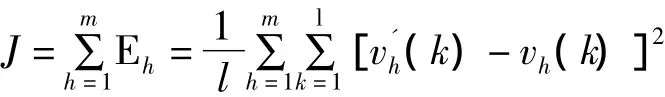
应用蚁群算法找到一组PID神经元网络的初始权值，蚁群优化的目标是使PID神经元网络控制系统输出误差平方均值为J最小。数目s=45，通常蚂蚁数量，其中n为问题的规模，此处n=45，所以蚂蚁数量M在7～22之间取值，ρ值的选取通常在0.5～0.7之间算法的性能较为稳定，需要根据仿真实验的结果适当调整参数大小。通过大量仿真实验结果分析，信息素残留系数ρ=0.7，蚂蚁数量M=13时蚁群优化PID神经元网络权值初值效果最好。ρ=0.7，M=13时的优化曲线如图2所示。

式中，变量个数m=3，采样点数l=500。

蚁群算法中最大迭代次数 NCmax=50，集合内的随机数个数N=30，信息素强度Q=10，由于PID神经元网络采用三输入、三输出的形式，所以权值

图2 ρ=0.7，M=13时的优化曲线

为检验系统的性能，将经蚁群算法优化得到的PID神经元网络权值带入到网络中，在t=0时刻采用单位阶跃输入对PID神经元网络进行训练，系统的响应情况如图3、图4、图5所示。

由以上仿真结果可以看出，因为控制器的初值由蚁群算法训练，减少了在线调整的计算量和调整时间。蚁群PID神经元网络有良好的控制品质，优于PID神经元网络控制算法。

4 结论

应用基于蚁群算法的PID神经元网络控制器对球磨机制粉系统进行控制仿真，采用蚁群算法优化PID神经元网络的初始权值，在一定程度上避免了PID神经元网络收敛速度慢，易于陷入局部极小点的缺陷，实现了球磨机制粉系统的控制效果。

图3 单位阶跃扰动下出口温度的响应曲线

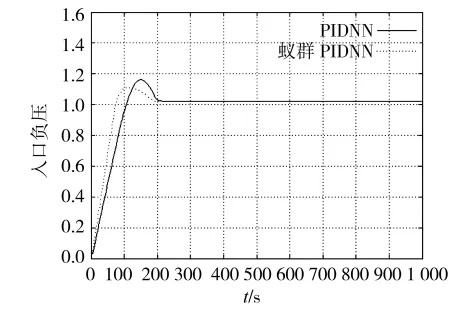
图4 单位阶跃扰动下入口负压的响应曲线

图5 单位阶跃扰动下磨负荷的响应曲线

［1］ 刘全伟，周洪.钢球磨煤机的模糊神经元解耦控制方法［J］.华北电力技术，2001，7(1):34-36.

［2］ 张骁博，杨建国，赵虹.钢球磨煤机制粉系统运行优化的试验研究［J］.动力工程学报，2010，30(2):133-137.

［3］ 舒怀林，PID神经元网络及其控制系统［M］.北京:国防工业出版社，2006:21-38.

［4］ M Dorigo.Optimization，Learning and Natural Algorithms［D］. Ph.D.Thesis.Department of Electronics，Politecnico Milano，Italy，1992.

［5］ 段海滨.蚁群算法原理及其应用［M］.北京:科学出版社，2005:24-27.