坝后背管运行期温度影响研究

徐福卫，陈海玉

（襄樊学院建筑工程学院，湖北襄樊441053）

0 引言

三峡水电站左岸机组采用单管单机，为坝后式水电站。电站压力管道直径12.4 m。压力管道采用坝后背管布置型式，浅卧在下游坝面6.47 m深的预留槽内，即钢管埋入坝面以内1/3管径，压力管道的结构型式为钢衬钢筋混凝土联合受力。

坝后背管是一种有广阔发展前景的、经济、安全的水电站输水管道形式。它是一种钢板衬砌与外包钢筋混凝土联合承载的结构，钢衬的厚度可以较明管方案薄，并允许外包混凝土开裂（外包混凝土还可以防止钢管受严寒或日照等温度影响［1，2］），可充分发挥钢材的抗拉作用。工程布置上改变了传统的坝内埋管形式，将压力管道直接布置在下游坝面，从而减少了管道空腔对坝体的影响，减少了坝体施工与管道安装的交叉影响，有利于保证施工质量和进度。由于节省了高强钢板，在造价上相对经济些。

但是根据我国东江、五强溪、李家峡水电站的建设经验及专家讨论的情况，坝后式压力管道在运行期间由于受管道内部水体和外界（如日照）温度的影响，管道内外层经常会出现一种内层温度较低而外层温度较高的温度场（以下简称内低外高温度场）。所产生的温度荷载对压力管道开裂断面钢材应力和混凝土裂缝宽度的开展是否有影响，影响程度如何，目前研究得仍不透彻。温度影响问题是过去很长一段时间内工程上十分关注而又没有解决的问题，而裂缝控制问题则是钢衬钢筋混凝土压力管道重要的、难以解决的技术问题。因此，研究该温度场的温度荷载对管道应力场的影响对三峡水电站坝后式压力管道的正常运行有十分重要的意义。

本研究选取左岸厂房9号坝段作为典型坝段，计算采用非线性功能较强的大型通用软件ANSYS，建立了带裂缝工作管道的有限元分析模型，并与大比尺（1∶2）模型试验结果对照验证，对管道运行期常见的温度场（即管道内层温度较低而外层温度较高的温度场）对管道应力场的影响进行较为深入的分析，为三峡水电站的运行提供一定的参考。

1 有限元分析模型的建立

为了能和模型试验进行真实的数据对比验证，故有限元分析模型的尺寸依据武汉水利电力大学的大比尺（1∶2）模型［3］尺寸建立。

在建立有限元分析模型之前，首先要对模型试验裂缝进行简化。因为，在进行温度荷载下管道结构计算时，其结构形式与常规计算不同，此时管道是带裂缝工作的，可以说初始裂缝分布是建立计算模型的基础。图1给出的是模型试验进行温度荷载试验之前的裂缝分布状况。从裂缝的分布看，左右基本对称，管道上半圆部分裂缝分布较密，下半部分裂缝分布较疏。其中上半圆均匀分布裂缝11条，下半部分不均匀分布7条，靠近0°和180°处分布较密。

按照模型试验的实际尺寸建立了有限元模型，单元及网格划分见图2。考虑到模型及荷载的对称性，在建立模型时选取了管道结构的1/2。由于研究的重点在于管道，因此管道部分网格划分较密，坝体部分网格划分较疏。

在图2的有限元网格划分中，表面上看不出裂缝位置及粘结单元，因为裂缝处虽然是两个不同的节点，但位置是重合的；混凝土和钢筋之间的粘结单元也是同样的道理。

图1 有限元计算模型裂缝分布Fig.1 Cracks distribution in the FEM calculation model

图2 有限元计算模型单元及网格划分Fig.2 Elements and meshing in the FEM calculation model

图3为有限元模型材料分区及裂缝位置图，钢筋尺寸与模型试验用钢筋截面积相同，只是把圆形等效成了方形；钢衬厚度与实际相同。裂缝的位置与图2裂缝位置相同。

应用有限单元法分析钢筋混凝土结构时，所得结果的可靠性很大程度上取决于材料模式的真实性。因此，为了获得符合实际的有限元分析结果，需要进行数值试验来不断验证、修正。下面结合图2和图3所示的有限元分析模型及其相应的材料分区分别说明在ANSYS中使用的单元及材料模式。

图3 有限元模型材料分区及裂缝位置图Fig.3 Material zones and cracks in the FEM model

（1）管道混凝土与坝体混凝土均采用ANSYS软件中的SOLID65单元，此单元是一个八节点、六面体单元，采用此单元后，单元所对应的材料为混凝土材料，混凝土材料计算参数见表1。

表1 混凝土材料参数表Table 1:Parameters of concrete

（2）钢筋作为实体单元而不是杆单元考虑。选用的是ANSYS软件单元库中的SOLID45单元，此单元为普通的八节点六面体单元。

（3）本章研究的重点是温度荷载对裂缝宽度与钢材应力的影响［4，5］，因此钢筋与混凝土之间的粘结单元是必须要考虑的，否则可能给结果带来很大的误差。经综合考虑，并根据以往使用ANSYS软件进行混凝土结构计算的经验，最终采取改进的粘结链单元。

（4）在模拟温度荷载对管道作用时，裂缝是根据模型试验结果预先设置的。考虑裂缝面传力方式［6，7］，裂缝的模拟采用ANSYS软件中的面-面接触单元。

（5）钢衬及其与混凝土接触模拟采用了八节点、六面体的块体单元，即SOLID45。

针对温度荷载下管道计算的有限元模型，表2对采用的单元、材料进行了汇总。

2 温度荷载有限元成果分析

根据以上建立的有限元模型进行运行期温度场的计算分析。计算时针对本温度场（内低外高）采用了三种不同的温度差，分别为7.35℃、14.00℃、19.50℃。

首先进行的是管道在三种温差下的温度场分布计算，这是进行温度荷载作用计算的基础。图4～6为管道在三种温度差时的温度等值线。

图4 温差为7.35℃时的管道温度场等值线Fig.4 Contour lines in the temperature field with temperature difference is 7.35℃

图5 温差为14.00℃时的管道温度场等值线Fig.5 Contour lines in the temperature field with temperature difference is 14.00℃

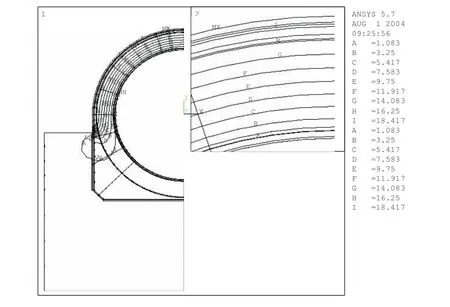
图6 温差为19.50℃时的管道温度场等值线Fig.6 Contour lines in the temperature field with temperature difference is 19.50℃

图7给出了模型试验与有限元分析的0°、45°、90°方向径向位移对比曲线，可以看出计算和试验结果基本吻合。从图8～10中曲线可以看出，在内低外高温差作用下，有限元计算结果与模型试验结果吻合得比较好。有限元计算结果均比模型试验结果小，误差基本在10%以内。

裂缝宽度的模拟结果见表3。在温度作用下，管道的缝宽变化数量级在10-3～10-4mm左右，因此无论是模型试验量测还是模型计算，其相对误差值较难控制。根据计算结果看出，有限元计算结果与模型试验结果在同一数量级。管道径向裂缝的中间部位计算值与量测值比较接近，但靠内部位数值相差较大。相差较大的主要原因为模型试验与有限元模拟的一个边界不同：裂缝接触面。表4中所示的模型管道外壁温度变化的计算位移和试验测量值是比较接近的。

图7 内低外高温差管道径向位移Fig.7 Radial displacement of the penstock with lower tempera⁃ture inside and higher outside

图8 管道0°裂缝断面钢材应力随温差变化曲线Fig.8 Relationship between steel stress and temperature with 0°crack

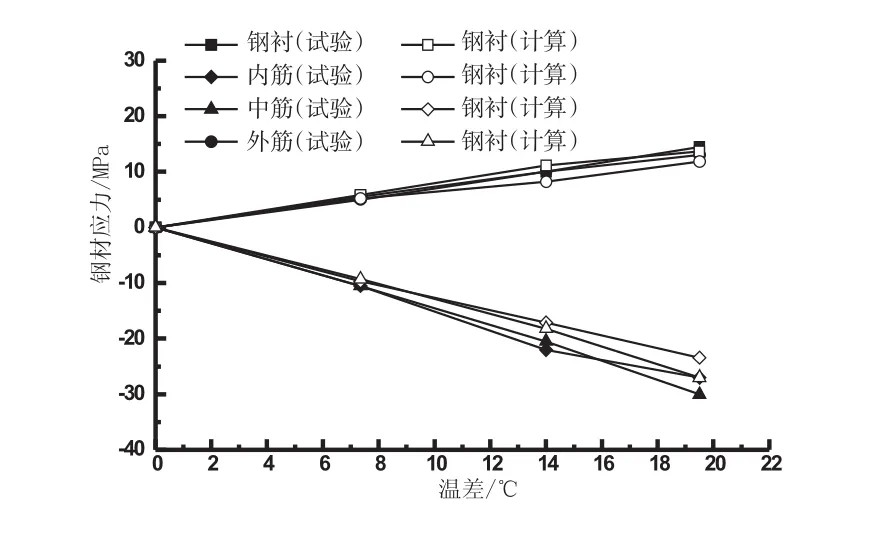
图9 45°裂缝断面钢材应力随温差变化曲线Fig.9 Relationship between steel stress and temperature with 45°crack

图10 90°裂缝断面钢材应力随温差变化曲线Fig.10 Relationship between steel stress and temperature with 90°crack

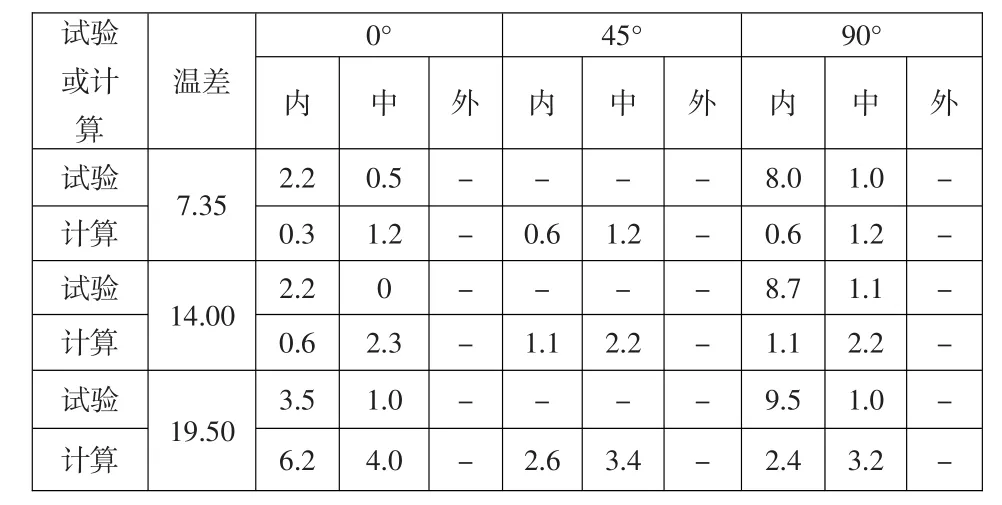
表3 模型裂缝宽度随温度变化成果对比表（单位：0.01 mm）Table 3:Relationship between crack width and temperature in the model

表4 模型管道外壁温度变化位移对比表（单位：0.01 mm）Table 4:Relationship between temperature change outside of the penstock and displacement in the model

从管道内低外高温度场作用下的有限元模拟结果可以看出，有限元模型是正确的，经受住了模型试验的检验。

3 结语

将以上有限元计算成果和模型试验成果进行对比，可以看出在内低外高温度场的作用下，有限元计算结果与模型试验结果吻合得比较好。

（1）针对钢衬钢筋混凝土压力管道建立了基于ANSYS分析软件的有限元计算模型，经过计算与实际模型试验的对比，验证了此有限元计算模型的可靠性，为以后此类结构运行期温度荷载作用的计算奠定了基础。钢衬钢筋混凝土压力管道在运行期受到的温度影响作用不可忽略，可以采用模型试验或者有限元模拟计算的方法得到温度荷载对缝宽与钢材应力的影响。

（2）值得注意的是，在内低外高温差作用下，管道裂缝中间部位的最大缝宽并不在管道的圆周中心线上，而是靠近管道内侧。从裂缝缝宽来看，中间部位的缝宽要大于靠近管道内部的缝宽。管道外侧裂缝处于闭合状态，对于钢筋的保护是有利的。■

[1]朱伯芳.有限单元法原理与应用（第二版）[M].北京:中国水利水电出版社,1998.

[2]伍鹤皋.水电站钢衬钢筋混凝土压力管道[M].北京:中国水利水电出版社,2000.

[3]武汉水利电力大学,葛洲坝水电工程学院,葛洲坝集团公司.三峡电站钢衬钢筋混凝土压力管道大比尺平面结构模型试验研究.1996.

[4]李德基,曾宪岳,张忠信.外露式钢筋混凝土压力管道温度应力计算方法探讨[J].水力发电学报,1984（02）：19～23

[5]董哲仁.钢衬钢筋混凝土压力管道混凝土裂缝温度张合量数学模型[J].水力发电,1996(5):29～33.

[6]董哲仁,董福品,鲁一晖.钢衬钢筋混凝土压力管道混凝土裂缝宽度数学模型[J].水力发电，1996（5）：39～42.

[7]李德基,曾宪岳,张忠信.钢筋混凝土压力管道开裂后断面内力计算方法探讨[J].水力发电学报,1987（2）:21～37.