攻角变化对超音速进气道再起动特性的影响①
赵湘恒,夏智勋,方传波,胡建新,王德全,游 进
(国防科技大学航天与材料工程学院,长沙 410073)
0 引言
进气道的起动/再起动特性直接影响飞行器的飞行包络和再起动能力。对于进气道的起动/再起动问题,国内外在数值模拟和试验研究上已经做了大量的工作。文献[1-7]即利用数值模拟和试验的方法对进气道的起动/再起动特性进行了深入研究。文献[8-9]研究了楔面转折角、壁面温度对高超音速进气道不起动/再起动特性的影响。文献[10]对攻角引起的高超音速进气道不起动/再起动特性进行了数值模拟研究,分析了不起动/再起动过程中进气道性能参数随来流攻角的变化规律,并对进气道再起动条件进行了讨论。文献[11]针对攻角动态对二元高超音速进气道气动特性的影响进行了数值模拟研究。文献[12]针对攻角动态变化对侧压式进气道起动特性的影响进行了风洞试验,研究了来流攻角变化频率等因素对进气道性能和起动特性的影响。但是,上述研究大都集中在稳态工况下,针对非稳态工况下的研究相对较少,对攻角变化引起的进气道再起动过程没有进行非稳态研究与深入分析。对于X型或双下侧布局的进气道,由于压缩型面的位置可能不同,当飞行器做大机动飞行时,很有可能造成其中某个或几个进气道陷入不起动,此时通过合理改变攻角即可实现进气道的再起动工作。
本文针对攻角变化对超音速进气道再起动特性的影响进行了研究,得到了攻角动态变化对超音速进气道再起动过程的影响规律,并对其成因进行了分析。
1 物理模型和计算方法
物理模型采用典型的二元混压式超音速进气道,其结构简图如图1所示,进气道压缩激波系由2道外压斜激波、1道唇口内压斜激波及结尾正激波组成。
进气道主要参数见表1,按等宽高比设计,则其实际宽度为92 mm。
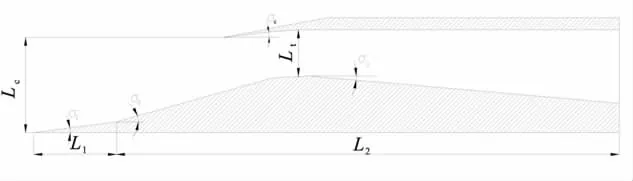
图1 二元混压式超音速进气道结构简图Fig.1 Sketch of the two-dimensional mixedcompression supersonic inlet
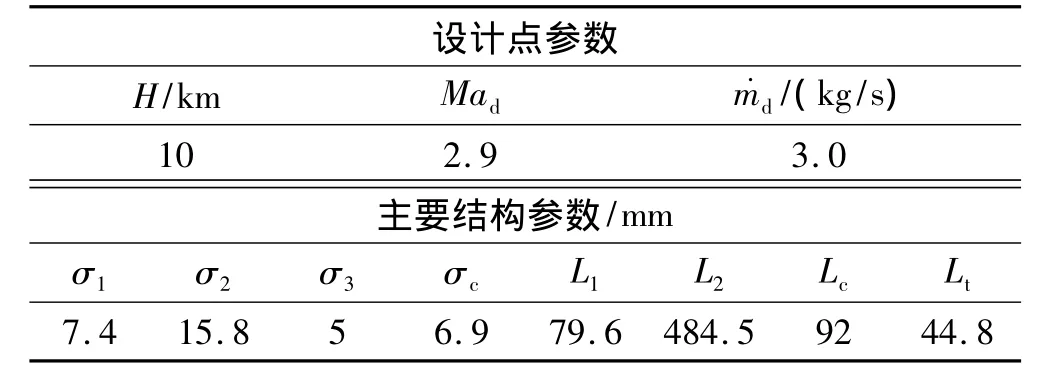
表1 进气道主要参数Table 1 Main parameters of the inlet
以二维非定常可压缩流的N-S方程为控制方程,采用FLUENT软件对流场求解,采用Roe-FDS计算格式,对流项采用二阶迎风格式,湍流模型为SSTk-ω模型。采用“双时间步”的二阶隐式格式求解非定常过程。
边界条件有压力远场、压力出口及绝热无滑移壁面3类。进气道出口边界条件采用压力出口,其他来流边界条件采用压力远场,并通过编写用户自定义函数(UDF)控制攻角变化规律。
计算收敛准则:各控制方程的残差至少下降3个数量级,同时全流场进出口流量保持稳定。
2 计算方法校验
为验证该计算方法对非定常超音速流动的处理能力,模拟了文献[13]中利用激波管产生的自由激波在环境大气层传播形成的非定常运动现象。实验条件:激波管内径φ24 mm,运动激波Mas=1.46。
图2为实验纹影图[13],图3为计算所得不同时刻的密度和压力等值线图。可看出流场内激波和膨胀波等结构,表明计算格式具有较高的空间分辨率。图4给出了计算所得轴线上激波位置随时间的变化曲线,并与文献[13]中的实验结果进行了定量比较。由图4可见,计算与实验结果符合较好,表明计算格式具有足够高的时间精度。
通过校验表明,所用计算方法对非定常超音速流动问题的计算能力具有一定的可信度。

图2 激波管纹影图Fig.2 Schlieren photographs of the shock tube
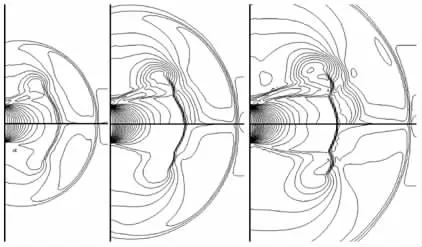
图3 计算的密度(上)和压力(下)等值线图Fig.3 Computational density(above)and static pressure(below)contours of the shock tube
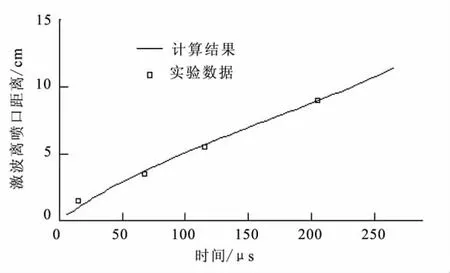
图4 激波位置随时间的变化Fig.4 Variation of the shock wave position with time
3 计算结果与讨论
3.1 稳态工况下攻角变化对进气道再起动特性的影响
进气道起动性能参数由数值模拟得到:设计高度时,进气道0°攻角对应最小马赫数Mamin=2.1,再起动马赫数Marestart=2.1。以Ma=2.1时不起动状态的进气道流场为初场,逐渐改变攻角至进气道再起动,考查稳态工况下不同攻角对应进气道性能的变化。
图5给出了-5°初始攻角的不起动流场转换至+5°过程中,同一背压、不同攻角下稳态工况对应的进气道流量系数(φ)和总压恢复系数(σ)。分析图5可得出,由-5°初始攻角变化至+2°的过程中,随着攻角的增大,进气道外压斜激波的激波角减小,导致激波压缩程度减弱,总压恢复系数下降;同时,由于进气道实际捕获面积逐渐减少,流量系数也随之降低。当攻角增大至+3°时,来流方向的气流分速度增大至某一值,进气道实现再起动,总压恢复系数迅速增大。继续增大攻角,已经起动了的进气道总压损失随来流方向的气流分速度增加而加大,但是,进气道实际捕获面积仍然持续减小,导致流量系数随之继续降低。

图5 稳态工况下对应攻角的进气道性能Fig.5 Performance of the inlet vs angle of attack in steady case
3.2 非稳态工况下攻角变化对进气道再起动特性的影响
3.2.1 攻角变化速率对再起动攻角的影响
对-5°初始攻角、Ma=2.1的不起动状态进气道,分别以 200、400、600、800、1 000°/s 的变化率改变攻角,实现进气道的再起动,考查攻角变化速率(α′)对进气道再起动攻角(α)的影响。
如图6所示,当进气道转换至某一攻角时,内收缩段前的“λ”形激波贴于唇口,分离区较小但尚存在,唇口上方亚音速溢流消失。此即通常所指的再起动临界状态,对应攻角即再起动攻角。
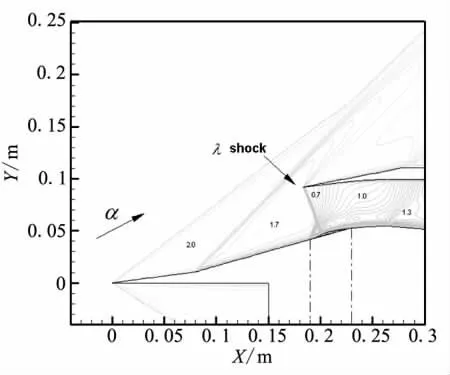
图6 进气道再起动临界状态Fig.6 Critical restarting state of the inlet
以图6所示的再起动临界状态为基准,图7给出了不同攻角变化速率下,进气道到达再起动临界状态对应的再起动攻角及其所需响应时间(t)。结合稳态工况算例分析可知,攻角变化速率越大,非稳态工况下进气道再起动攻角与稳态工况下再起动攻角差别越大,再起动攻角随攻角变化速率的增加而加大,但响应时间随之减小。
3.2.2 攻角变化速率对再起动过程中进气道性能的影响
图8给出了不同攻角变化速率下,进气道由Ma=2.1、-5°攻角的不起动流场转换至同一攻角 0°时,同一背压下对应的流量系数和总压恢复系数。图8中流量系数采用进气道出口质量流量与以自由来流参数通过捕获面积的空气质量流量之比。由图8可知,当攻角变化速率相对较小时,同一攻角下对应的流量系数和总压恢复系数与稳态攻角下相比变化不大,但随着攻角变化速率的增大,两者与稳态攻角下相比均有不同程度的下降。
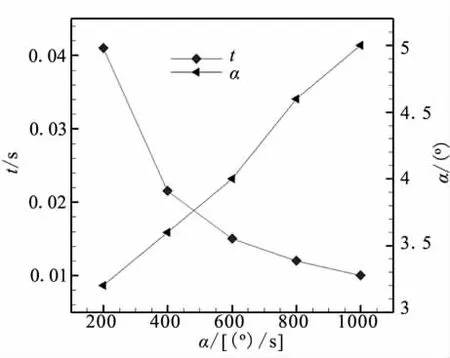
图7 再起动攻角及响应时间随攻角变化速率变化曲线Fig.7 Restarting angle of attack and responding time vs the changing rate of angle of attack
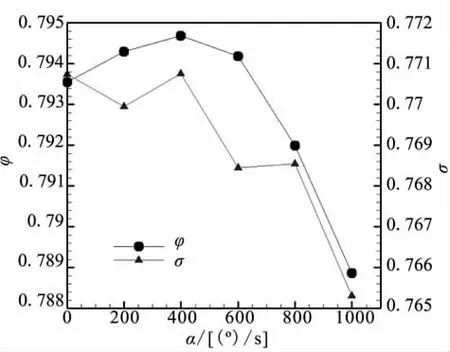
图8 不同攻角变化速率下的进气道性能(α=0°)Fig.8 Performance of the inlet vs the changing rate of angle of attack(α =0°)
以α'=400、1 000°/s为例,保持进气道出口背压不变,图9给出了不起动的进气道流场由-5°初始攻角增加至+5°后保持不变的再起动过程中流量系数和总压恢复系数的变化。图9中,流量系数仍取进气道出口质量流量与以自由来流参数通过捕获面积的空气质量流量之比,tr表示从不起动初场到达再起动临界状态所需响应时间。
由图9(a)、(b)可知,在由负攻角转换至正攻角过程中,进气道流量系数和总压恢复系数先下降至某一值,到达再起动临界状态之后迅速增大,然后以波幅呈衰减趋势的形式波动,最后趋于稳定。整个过程中,进气道性能参数变化趋势与稳态计算结果基本一致。按照稳态条件下的定义,进气道越过再起动临界状态后,流量系数为一定值,但是非稳态工况下,从再起动临界状态至流场基本稳定期间,流量系数和总压恢复系数均有几十毫米的响应波动。
图9(c)对应 Ma=2.3、α'=400°/s的再起动过程中,进气道流量系数和总压恢复系数变化。此时,来流速度已大于0°攻角下对应的再起动马赫数。由图9(c)可见,由于来流速度相对增加,进气道到达再起动临界状态所需的响应时间也随之减小;自再起动临界状态之后,进气道出口流量和总压同样呈现一定的波动,最后趋于稳定,但是稳定后的进气道性能与初始稳态性能相比差距较大。
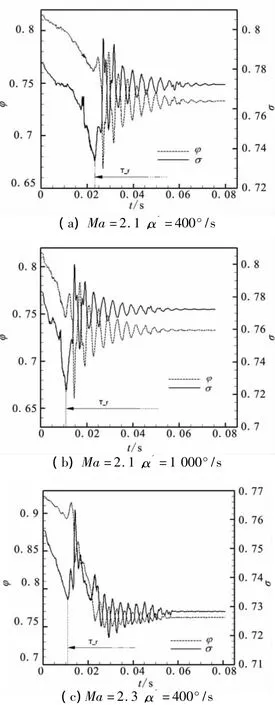
图9 再起动过程中进气道性能Fig.9 Performance of the inlet during restarting process
3.3 非稳态攻角变化对进气道再起动特性的影响分析
为分析造成不同攻角变化速率下进气道再起动特性的差异,以 α'=200、1 000°/s为例,图10进一步给出了进气道由-5°初始攻角的不起动流场转换至0°攻角瞬间的等马赫数流场云图。
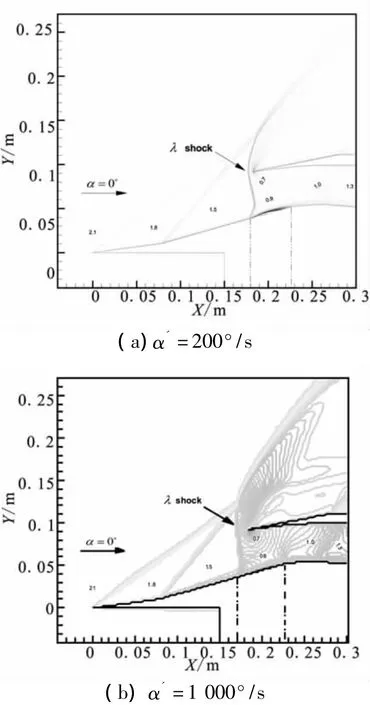
图10 再起动过程中进气道等马赫数云图(α=0°)Fig.10 Mach number contours of the inlet during Restarting process(α =0°)
对比两流场可明显看出,不同攻角变化速率时,“λ”形激波前的超音速流场区域特征基本相同,而进气道内收缩段前的亚音速分离区位置、大小及“λ”形激波后的亚音速溢流特征都有所差别:较大攻角变化速率时,分离区位置相对靠上游,范围也较大。由理论分析可知,相比亚音速流场而言,超音速流场对扰动的响应较快,当攻角变化速率相对较小时,亚音速流场区域响应比较及时,因而分离区和“λ”形激波能够及时对来流变化做出响应,进气道再起动攻角与稳态工况相比相差不大,而较大的攻角变化速率使得内收缩段前的亚音速流场响应相对延迟,造成进气道再起动攻角增加。
为分析进气道出口流量和总压波动变化的成因,图11给出了图9(a)中进气道总压恢复系数对应波谷时刻及其相邻2个波峰时刻的压力流场云图。由图11分析可知,自进气道到达再起动临界状态后的初始时间段内,结尾激波在扩压段内仍在不断演化,波后高压区强度和位置也有所不同。在对应出口总压处于波谷时刻(t=0.033 5 s),结尾激波的波后高压区压力相对较小,位置靠上游,而在对应出口总压处于波峰的2个相邻时刻(t=0.031 6、0.035 4 s),结尾激波的波后高压区压力相对较大,位置相对靠下游。造成这种现象的原因可能是工况变化的来流与扩压段激波边界层干扰造成的亚音速分离区之间的粘性作用使得气流与背压的匹配需要一个时间过程。
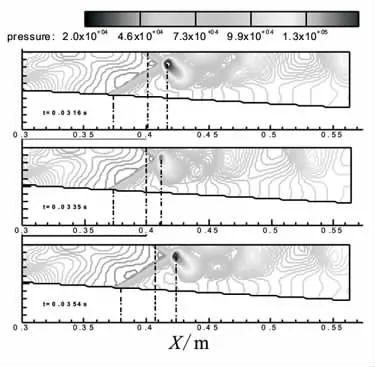
图11 扩压段等压强云图Fig.11 Static pressure contours of subsonic diffuser
4 结论
(1)当超音速进气道陷入不起动状态时,可通过合理改变攻角实现进气道的再起动工作。
(2)超音速进气道的再起动攻角随攻角变化速率的增大近似成线性增加。
(3)攻角变化速率较小时,相同攻角下超音速进气道性能与稳态工况下对应性能差别较小;攻角变化速率较大时,非稳态与稳态工况下相同攻角对应的超音速进气道性能差别较大。
[1]Van Wie D M,Kwok F T,Walsh R F.Starting characteristics of supersonic inlets[R].AIAA 96-2914.
[2]Tahir R B,Molder S.Unsteady starting of high Mach number air inlets-A CFD study[R].AIAA 2003-5191.
[3]李璞,郭荣伟.一种高超声速进气道起动/再起动的数值研究[J].航空动力学报,2010,25(5):1049-1055.
[4]袁化成,梁德旺.高超声速进气道再起动特性分析[J].推进技术,2006,27(5):390-398.
[5]王成鹏,程克明.高超进气道临界起动特征[J].航空动力学报,2008,23(6):997-1002.
[6]丁海河,王发民.高超声速进气道起动特性数值研究[J].宇航学报,2007,28(6):1482-1487.
[7]谢旅荣,郭荣伟.一种定几何混压式二元进气道的再起动特性研究[J].航空动力学报,2008,23(2):389-395.
[8]常军涛,于达仁,鲍文,曲亮.楔面转折角对高超声速进气道不起动/再起动特性的影响[J].固体火箭技术,2009,32(2):135-140.
[9]范轶,常军涛,鲍文.壁面温度对高超声速进气道不起动/再起动特性的影响[J].固体火箭技术,2009,32(3):266-270.
[10]常军涛,于达仁,鲍文.攻角引起的高超声速进气道不起动/再起动特性分析[J].航空动力学报,2008,23(5).
[11]刘凯礼,张堃元.迎角动态变化对二元高超声速进气道气动特性的影响[J].航空学报2010,31(4):709-714.
[12]郭斌,张堃元.攻角动态变化对侧压式进气道起动特性影响的风洞试验[J].航空动力学报,2009,24(10).
[13]Miss Y K Lee,Shum P T.The instability of axisymmertric supersonic jet impinging on flat plate[R].Report of Department of Aeronautical Engineering,University of Bristol,June 1983.

