基于神经网络的期铜价格趋势预测研究

王书平，徐小飞

(北方工业大学 经济管理学院，北京 100144)

自上海金属交易所成立以来，我国的期铜市场经历了不平常的发展之路，经过了两次大的结构性调整，所有的这些都给期铜预测带来了困难。在期铜价格预测方法研究中，计量经济模型占主流的地位。赵建伟等[1]运用GARCH、EGARCH、FIGARCH、FIEGARCH等四种模型，对沪铜期货价格的波动率进行了预测，分析表明，FIGARCH模型预测效果最好，其次是GARCH模型。刘轶芳等[2]在EWMA和GARCH模型思想的基础上，提出基于GARCH-EWMA的期货价格预测模型，为期货市场合约价格的预测提供了新的预测方法。在这些计量经济期货预测模型中，比较成熟的是AMIMA预测模型，例如，王习涛[3]在ARIMA模型的基础上通过对原始数据进行局部平稳化处理，在一定程度上减小了预测误差，提高了预测精度。陈林、黄章树[4]利用ADF检验确认序列的平稳性，并确定差分次数，运用枚举法确定最优的自回归滞后项数和滑动平均项数，从而提高了ARIMA模型对期铜价格预测的精度。

然而，由于期铜价格系统内部结构的复杂性、外部因素的多变性，使得期铜价格呈现出非线性性、动态性等特征，传统的预测方法已不能满足期铜价格预测的需要。近年来，神经网络开始兴起。Grudnitski[5]应用神经网络对S&P指数期货和黄金期货的价格进行了预测；Dematos[6]基于前馈神经网络模型对日元汇率进行了预测。越来越多的学者寄厚望于神经网络强大的非线性预算能力和学习能力，试图找出一条期铜价格预测的可行性方法。例如，向小东综合小波分析和传统神经网络的优点，采用小波神经网络方法对石油期货价格进行了预测；杨熙亮等分析了原有期货价格时间序列的特点和规律，采用一种改进的BP神经网络建立时间序列预测模型，对布伦特原油期货价格进行了预测研究，结果表明，BP神经网络具有良好的自组织性和自适应性，用它做期货价格预测是行之有效的；杨君岐基于Elman神经网络分别对股票短期及中长期价格变化建立了动态预测模型。

上述分析表明，在金融市场的非线性预测中，神经网络是一种比较合适的方法。本文试图建立适合于我国期铜价格预测的神经网络模型，分别构建了BP、RBF、Elman动态神经网络模型，并进行实证分析和对比研究。

一、神经网络模型的选取

现有的人工神经网络模型中具有代表性的是多层前向神经网络，常用的多层前向网络有BP网络和径向基函数RBF。而Elman动态神经网络由于添加了一个承接层对隐层的输出进行延迟和存储后，自联到隐层的输入，从而增加了网络处理动态信息的能力。

误差反向传播BP网络是一个采用误差梯度下降法进行学习的多层网络，其学习采用监督的学习方法，可以将一个具有一个sigmoid函数层，一个线性函数输出层的网络拟合出反映历史的时序数据之间的模型，从而完成对走势的预测。

径向基函数RBF是一种单隐层前馈网络，它采用高斯(Gaussian)型基函数来实现输出层同隐层之间的映射，输入层节点只传递输入信号到隐层，隐层的基函数为线性的，隐节点是由辐射状作用函数构成，输出单元是线性的，即输出单元对隐节点输出进行线性加权组合。整个网络是通过非线性基函数的线性组合，实现从输入和输出的非线性变换，隐节点的作用函数对输入信号将产生局部响应，因此该网络具有局部逼近能力。

Elman神经网络是动态递归网络的一种，其基本思想是利用最小二乘法，采用梯度搜索技术实现网络的实际输出与期望输出的均方差最小化。它的主要结构是前馈连接和反馈连接两部分，前馈连接包括输入层、隐层、输出层和承接层，其中输入层的单元仅起信号传输作用，输出层单元起线性加权作用，隐层单元的传递函数可采用线性或非线性函数；反馈连接指的是承接层，它用来记忆隐层单元前一时刻的输出值，可以认为是一步延时算子。Elman神经网络的特点是隐层的输出通过承接层的延迟与存储，自联到隐层的输入，这种自联方式使对历史状态的数据具有敏感性，内部反馈网络的加入增加了网络本身处理动态信息的能力，从而达到动态建模的目的。Elman神经网络具有逼近能力优于一般的静态网络、收敛速度快的优点。

二、数据的来源和预处理

本文采用上海交易所三月期铜的月平均收盘价作为考察对象，考察期为1995年4月至2010年3月，共180个数据。期铜价格的单位为：元/吨。数据来源于RESSET金融研究数据库。

(一)X-12-ARIMA季节调整

近年来，随着生产商在期铜交易中的参与程度日益广泛，期货和现货价格联系也日益紧密，季节因素和随机干扰项等因素对铜价的影响越来越大，因此有必要对数据进行季节性调整，消除季节因素和随机项因素的影响。令月度时间序列为yt，t=1,…,n，n为观察个数。不妨使用乘法模型yt=TtStItDt进行分析，其中Tt,St,It,Dt分别表示趋势成分、季节成分、不规则成分和交易日因子。

X-12-ARIMA方法是目前最为流行和应用最广泛的季节调整方法，该方法包括两个阶段。在第一个阶段，建立regARIMA模型，形式如下：

(1)

其中，L是滞后算子，s为季节周期的长度(月度数据s=12，季度数据s=4),d、D分别表示非季节性差分阶数、季节性差分阶数，φp(L)、θq(L)分别表示非季节性p阶自回归算子、q阶移动平均算子，φP(Ls)、ΘQ(Ls)分别表示季节性P阶自回归算子、Q阶移动平均算子，ut为白噪声过程，Yt是原始时间序列，Xit是回归变量。(1)式通常用Box-Jenkins记法表示成(pdq)(PDQ)s，此模型用来对原始序列中存在的各种离群值和历法效应作预调整，并对预调整后的序列向前预测和向后预测。在第二阶段，将前一阶段产生的时间序列回归误差导入X-11模块进行季节调整，将序列分解成趋势成分、季节成分、不规则成分和交易日成分。

本文采用该方法对对期铜价格时间序列进行季节调整，去除原始序列中的季节成成分和不规则成分，只保留了趋势循环成分，结果如图1所示。从图中可以看出，经过处理后的序列过滤掉了原始序列的高噪音部分，使得整个序列变得更加平滑，而且依旧保留了原始时间序列的全局变化趋势。

(二)数据的归一化处理

在建立神经网络预测模型之前，首先要将数据进行归一化处理。所谓的归一化就是指将数据转化成有利于神经网络收敛的数据，其值在区间[0、1]或[-1、1]里。归一化的公式如下：

(2)

其中，xi为季节调整后的数据，Xi为归一化处理后的数据，xmax、xmin分别为季节调整后数据中的最大值和最小值。

(三)样本的产生

本文将对期铜价格进行多步预测。多步预测又称迭代单步预测，既先进行单步预测，然后将输出反馈给输入端作为网络输入的一部分。假定时间序列为

X={xi|xi∈R,i=1,2,…,L}

(3)

通过序列的前N个时刻的值，预测出后M个时刻的值。这里可采用序列的前N个时刻的数据为滑动窗，并将其映射为M个值。这M个值代表在该窗之后的M个时刻上的预测值，表1列出了数据的划分方法。该表把数据分为K个长度为N+M的、有一定重叠的数据段，每一个数据段可以看做是一个样本，这样就可得到K=L-(N+M)+1个样本，这样就可以将每个样本的前N个值作为神经网络的的输入，后M个值作为目标输出，通过学习，实现从RN到输出空间RM的映射，从而达到时间序列预测的目的。依据这种方法，本文将前160个数据作为训练数据，后20个为预测和评价数据，将N定为5，M定为1，这样就产生了176个子样本，其中前156个样本作为训练样本，后20个样本作为测试样本。

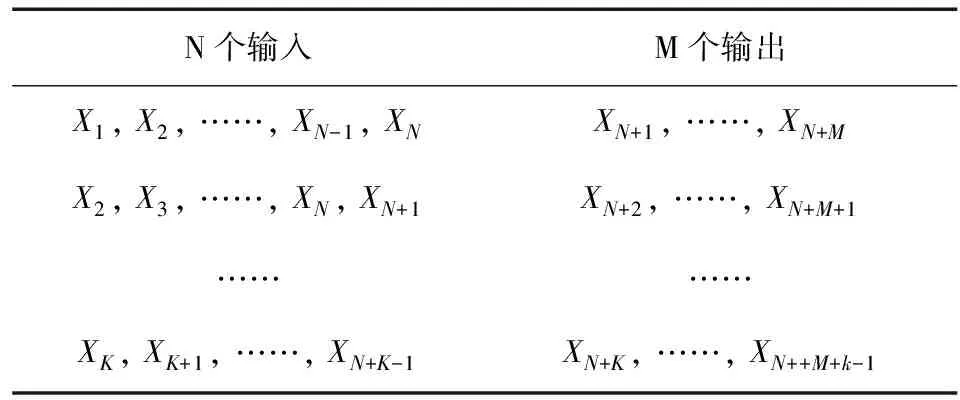
表1 样本产生过程

二、实证分析

(一)节点数和隐层数的确定

本文利用Matlab软件的Neural Network工具包，对季节调整后的期铜价格数据，分别用BP、RBP及Elman函数进行了测试。

输入和输出层节点数的确定。由于本文采用多步预测方法，并且将N定为5，M定为1，这样就确定了神经网络预测模型的输入层节点数和输出层节点数分别为5和1。

隐层数和隐层节点数的确定。理论分析已经证明，具有单隐层的前馈网可以映射所有的连续函数，为了便于对比，本文所选用的三个神经网络都采用单隐层神经网络模型，而初始隐含层的神经元节点数依据公式(4)给出。

(4)

其中，m为隐含层神经元节点数；n为输入层神经元节点数；l为输出层神经元节点数；a是1-10之间的整数。

经过测试，BP网络采用5-16-1、RBF网络采用5-19-1、Elman网络采用5-10-1网络结构，其效果最理想。

(二)预测效果比较

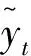
(5)

此指标反映预测的平均相对误差程度。预测的均方误差根为：

(6)

此指标反映预测的平均绝对误差程度。预测的趋势命中率为：

(7)

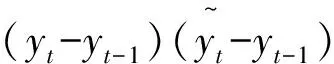
对于一个预测方法，这三个指标中的MAPE和RMSE越小而TR越大，则说明预测效果越好。表2给出了各方法预测铜价趋势的三个评价指标值(表中MAPE和TR的数值为百分比数)

表2 预测效果比较

由表2可以看出，在铜价趋势预测中，BP、RBF、Elman神经网络预测方法的平均绝对百分比误差和均方误差根两个指标都优于ARIMA方法，趋势命中率都逊于ARIMA方法；Elman方法无论从迭代次数和预测效果上明显优于传统的BP神经网络，平均绝对百分比误差缩小了9.15%，均方误差根缩小了4437，趋势命中率比BP方法明显要高；而和RBF方法相比，Elman方法的三个指标都优于RBF；三种神经网络模型的平均绝对百分比误差都低于20%，这在长期预测中是可以接受的，结果令人满意。

四、结论

本文利用X-12-ARIMA模型对上海交易所三月期铜价月平均数据进行了季节调整，将铜价的主体趋势分离出来，消除了季节因素、不规则等因素对铜价的影响，并分别构造了ARIMA、BP、RBF、Elman神经网络模型对季节调整后铜价趋势序列进行了预测。通过实证分析可以得出以下结论：

(1)通过BP、RBF、Elman神经网络模型和ARIMA模型的预测效果对比可以看出：神经网络模型在期货价格的预测上明显优于ARIMA模型，这要得益于神经网络模型强大的非线性逼近能力和强大的容错能力。

(2)由于Elman神经网络加入了内部反馈信号，利用内部状态反馈来描述系统的非线性动力学行为，从而提高了学习速度，在动态系统的预测上要优于一般的静态网络。因此，用Elman神经网络进行期铜价格预测可以取得比较好的效果。

[参考文献]

[1]赵伟雄，崔海蓉，何建敏.GARCH类模型波动率预测效果评价—以沪铜期货为例[J].西安电子科技大学学报(社会科学版)，2010，20(4)：27-32.

[2]刘轶芳，迟国泰，余方平，等.基于GARCH-EWMA的期货价格预测模型[J].哈尔滨工业大学学报，2006，38(9)：1572-1575.

[3]王习涛.ARIMA模型在期货交易预测中的应用研究[J].微计算机信息，2006，22(3)：1572-1575.

[4]陈林，黄章树.基于ARIMA模型的期货价格分析与预测[J].福州大学学报，2010(3)：32-37.

[5]Grudnitski, G.and Osburn, L.Forecasting S&P and gold futures prices: an application of neural networks.[J].Futures Markets, 1993, 13: 631-643.

[6]Dematos, G.Boyd, M.S.Kermanshahi, B.Fee.Forward versus recurrent neural networks for forecasting monthly Japanese Yen exchange rates[J ].Asia-Pacific Financial Markets, 1996, 3(1): 59-75.

[7]向小东.小波神经网络预测方法在石油期货价格预测中的应用[J].技术经济, 2006, 12(6)：121-124.