用SAS软件实现偏比例优势模型

毕秀媛 钱占成 冯国双

比例优势模型(proportional odds model)是处理有反应资料的常用方法〔1，2〕，目前在国内医学领域已有较多应用〔3，4〕。但该法必须满足比例优势假定条件，即自变量的回归系数应与分割点k无关。尽管以往有研究认为，比例优势模型对这一条件并不敏感〔5〕，但实际情况可能并非如此。Bender曾对此做过讨论〔6〕，如果不满足比例优势假定条件，比例优势模型跟其他模型的结果可能相反。Lall建议〔7〕，对假定条件不满足的数据，可采用偏比例优势模型(partial proportional odds model)进行分析，而不是比例优势模型。本文通过对一组有序反应变量的分析，介绍如何利用SAS软件实现偏比例优势模型的分析。?

偏比例优势模型简介

比较一下可以发现，偏比例优势模型与比例优势模型的不同之处在于多了γ系数。γ系数仅当自变量不符合比例优势假定条件的情况下才存在，如果所有自变量均满足该假定条件，则γ系数均为0，此时就是普通的比例优势模型。

偏比例优势模型的分析首先要定义一个新变量，代表不同分割点(k个等级共有k-1个分割点)，并分析自变量在不同分割点情况下的参数估计。γ系数反映了在不同分割点的情况下，在回归系数β基础上的增加值。

由于定义了k-1个分割点变量，每一观测的反应变量不再是1个，而变成了k-1个。因此可利用SAS proc genmod命令中的GEE(generalized estimating equations)算法来实现多结果变量的分析。

偏比例优势模型的SAS分析

本文数据来源于某关于胃癌病变的影响因素研究，从中随机选择48例作为示例分析。因变量y为胃癌病变，分为浅表性胃炎(SG)、萎缩性胃炎(CAG)、肠上皮化生(IM)、异型增生(DYS)，分别用 0、1、2、3 表示。自变量x1、x2分别为基因A和基因B，均为二分类变量，0表示表达阴性，1表示表达阳性。欲分析x1、x2对 y的影响。

首先我们采用比例优势模型分别对x1和x2进行分析，结果发现，x1不满足比例优势假定(χ2=12.6659，P=0.0018)，x2满足比例优势假定(χ2=2.0151，P=0.3651)。因此我们采用偏比例优势模型，对不同分割点的x1进行参数估计。

分析程序如下:

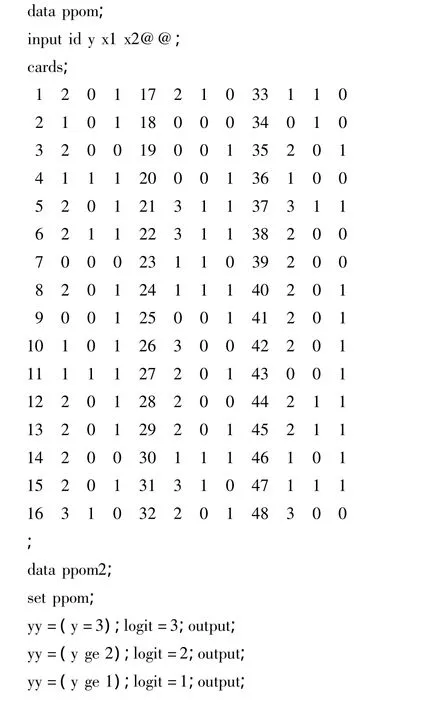
run;

/*上段程序对每一观测创建3个logit，logit表示分割点，分别为3、2、1，新的反应变量yy赋值为1和0，每一观测均有3个反应变量*/

proc genmod desc;

class id logit;

model yy=x1 x2 logit logit*x1/link=logit dist=bin type3;

repeated subject=id/type=un;

run;

/*上段程序利用proc genmod命令调用GEE算法，此时每一观测包含3个反应变量。由于X1不满足比例优势假定条件，因此加入logit*x1，分析不同logit下x1的参数估计。作业相关矩阵类型选择un，即无结构相关*/

主要输出结果分别见表1和表2。表1给出了参数估计结果。其中X1对应的是以3为分割点(0，1，2 vs 3)的参数估计值，由于程序中加入desc选项，因此实际反映的是(3 vs 0，1，2)的参数估计。由于参数估计值为1.7869，表明基因A阳性发生DYS的危险高于基因A阴性。X1*logit1、X1*logit2分别对应以1、2为分割点的X1估计值的增加值。也就是说，分割点为2(0，1 vs 2，3)时(实际为 2，3 vs 0，1)X1的参数估计值为1.7869－2.2501=－0.4632，表明基因A阳性发生DYS和IM的危险低于基因A阴性。分割点为1(0 vs 1，2，3)时(实际为 1，2，3 vs 0)X1的参数估计值为1.7869－0.2004=1.5865，表明基因A阳性发生DYS、IM和CAG的危险高于基因A阴性。

logit与此类似，Intercept反映的是 logit3的估计值，即分割点为3时的截距项。logit1反映了分割点为1时的截距项，其参数估计值为－2.2729+3.9428=1.6699。logit2反映了分割点为2时的截距项，其参数估计值为－2.2729+3.3225=1.0496。

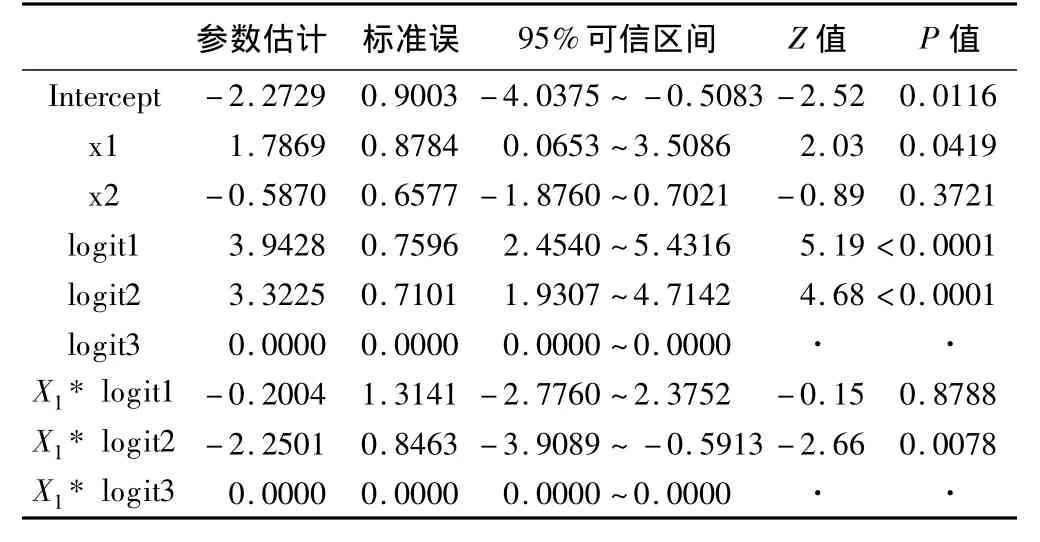
表1 参数估计结果

表1的参数估计结果显示，以不同分割点对因变量进行划分，其参数估计值相差较大。以3为分割点时，X1的影响有统计学意义(P=0.0419)。以2为分割点时，X1也有统计学意义(P=0.0078)。以1为分割点时，X1无统计学意义(P=0.8788)。而如果直接采用比例优势模型，结果显示X1无统计学意义(P=0.1841)。

表2给出了score得分检验，结果显示，X1*logit有统计学意义，提示不同分割点的X1估计值不同，进一步验证了x1不符合比例优势假定条件。

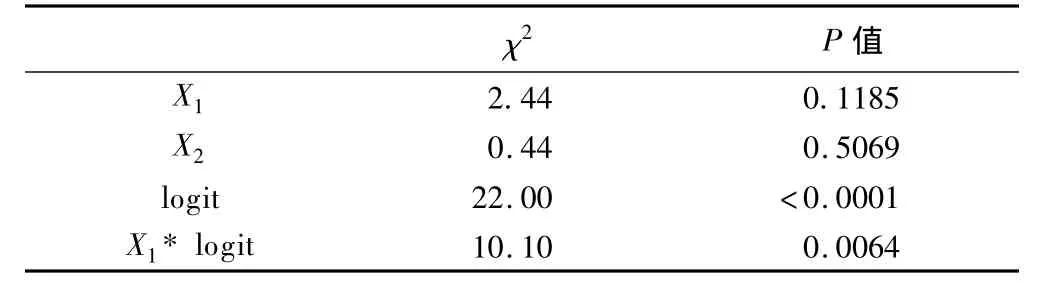
表2 Score得分检验

表3列出了偏比例优势模型与比例优势模型的参数估计比较结果。可以看出，两种模型的X1估计值差别较大。对于偏比例优势模型而言，不同分割点的X1估计值差别很大，当j=3和j=2时，出现了截然相反的结果，这也正是比例优势模型失效的原因。

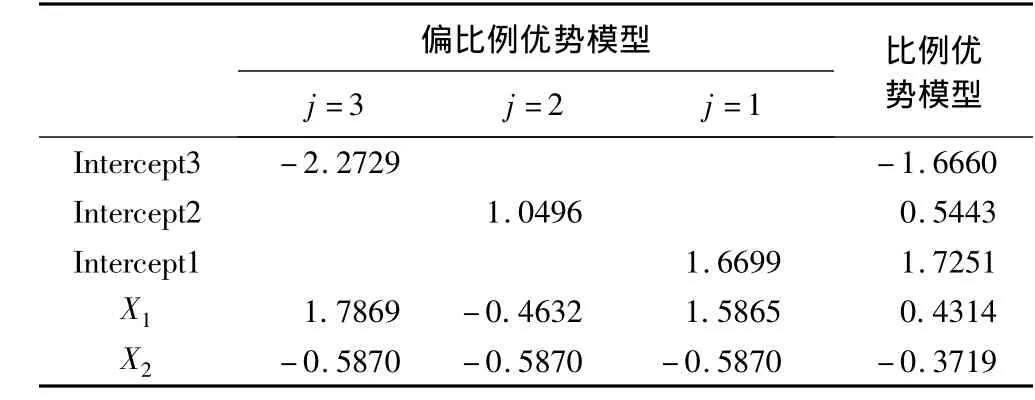
表3 比例优势模型与偏比例优势模型的参数估计比较

讨 论

有序分类资料最常用的分析方法是比例优势模型，目前该模型在国内不少领域都有应用，但关于其正确应用的探讨却很少。比例优势模型的前提条件是自变量的回归系数与分割点无关，也就是要求不同分割点的回归系数相同。只有满足这一条件，模型的估计结果才是比较可靠的。但在实际中这一条件并不总是能满足，尤其自变量较多的情况下，很难保证每一自变量都符合这一条件。此时如果采用比例优势模型是不妥的，而应选择其他更为合适的模型。Bender认为〔6〕，比例优势假定条件不满足时，可用独立的二分类模型(separate binary model)或偏比例优势模型进行拟合，且偏比例优势模型效率高于独立的二分类模型。偏比例优势模型实际上也是基于累积logit的一种方法，可利用GEE算法来实现〔8，9〕。以往由于受统计软件功能的限制，偏比例优势模型的实现较为困难。目前包括SAS软件在内的很多统计软件均可实现GEE算法，因此偏比例优势模型可作为比例优势假定条件不满足时的首选替代方法。

偏比例优势模型主要有两种:非限制的偏比例优势模型(unconstrained partial proportional model)和限制的偏比例优势模型(constrained partial proportional model)。非限制的偏比例优势模型中，符合比例优势假定的变量在不同分割点有相同的参数估计，不符合假定条件的变量在不同分割点有不同的参数估计。限制的偏比例优势模型中，假定自变量的参数估计在各分割点有一定的趋势(如线性趋势)，该模型一般需要事先对估计值有一定的了解，或者可以先通过非限制的偏比例优势模型估计出参数值，然后看是否有一定的趋势。

本文所介绍的是非限制的偏比例优势模型及其分析过程，这一模型也是实际中较为常用的。目前国内关于该模型的介绍极少，本文旨在抛砖引玉，以便进一步推动该模型的应用。

1．Amstrong BG，Sloan M．Ordinal regression models for epidemiologic data ．Am J of Epodemiology，1989，129(1):191-204．

2．Bender R，Grouven U．Ordinal logistic regression in medical research．Journal of the Royal College of Physicians of London，1997，31(5):546-551．

3．吴彬，田俊，罗仁夏．胃癌患者生存质量影响因素的累积比数模型分析．中国卫生统计，2007，24(1):36-38．

4．吴彬，曹建平，宋建华，等．福州地区高校教师亚健康影响因素的累积比数模型分析．中国卫生统计，2010，27(3):262-264．

5．李康，郭祖超，胡琳，等．有序分类数据回归模型及医学应用．中国卫生统计，1992，9(6):52-54．

6．Bender R，Grouven U．Using binary logistic regression models for ordinal data with non-proportional odds．Journal of Clinical Epidemiol，1998，51(10):809-816．

7．Lall R，Campbell MJ，Walters SJ，et al．A review of ordinal regression models applied to health-related quality of life assessments〔j〕．statistical methods in medical research，2002，11(1):49-67．

8．Peterson B，Harrell F．Partial proportional odds models for ordinal response variables．Appl Statist，1990，39(2):205-217．

9．Bender R，Benner A．Calculating ordinal regression models in SAS and S-plus ．Biometrical Journal，2000，42(6):677-699．