截尾分位数回归及其在生存分析中的应用*

王 娟 王 彤

在传统的生存分析中，多因素分析常采用Cox比例风险回归模型和加速失效时间模型，Cox比例风险回归模型要求资料满足等比例风险假定和对数线性假定，加速失效时间模型要求资料分布已知。但医学研究中，某些资料不满足上述要求，特别当观察值中有离群点(outliers)，所拟合的回归方程因“迁就”这个(些)离群点而使整体的拟合结果产生不同程度的偏离，以致影响了稳定性;再者，当总体存在异方差，即y的条件分布中方差不为常数时;或者研究兴趣在于分布在尾端区域数据的建模，亦不宜用Cox比例风险回归模型和加速失效时间模型。本文介绍一种适合于当生存资料不满足上述条件时的回归方法——截尾分位数回归。

原理与方法

所谓截尾分位数回归(censored regression quantiles，CRQ)，就是根据估计(生存时间的对数形式)的分位数，其模型为:

QY|X(τ，x)=xβ(τ)

与加速失效时间模型不同的是，QY|X(τ，x)表示给定x的条件下，y的第τ分位数的估计值。其中τ的取值范围为0＜τ＜1，当τ=0.5时，截尾分位数回归就是中位数回归(median regression)。截尾分位数回归中，参数估计一般用加权最小一乘(weighted least absolute，WLA)准则，即使目标函数:

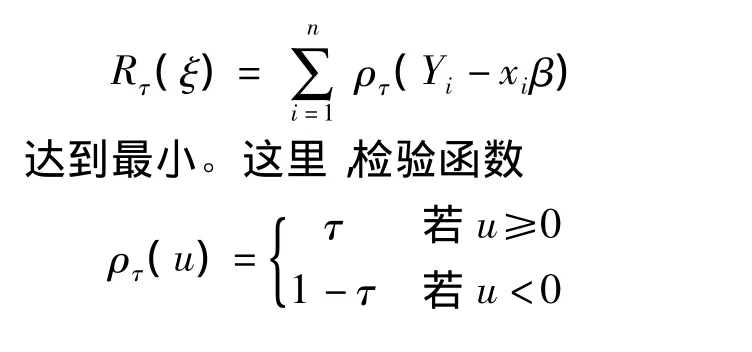
模拟分析

1．满足参数模型假定的模拟分析

如果生存时间服从指数分布，既能建立加速失效时间模型log(t)=+x+ε，又能建立比例风险回归模型 h(t，x)=h0(t)exp(x'β)，且两个模型中回归参数的相互关系为= － β〔2〕。

模拟方法如下〔3〕:模拟的样本含量为200，截尾比例为20%、40%、60%。首先产生服从(0，1)均匀分布的随机数S，令生存函数S(t)=S，同时产生服从N(0，1)的随机数作为自变量 x。令 β=1，利用 t=产生相应的生存时间t。产生服从B(200，0.2)的随机数作为截尾指示变量，这时截尾比例为20%。每次得到1000个模拟样本，分别采用Cox比例风险回归模型(Cox)、加速失效时间模型(AFT)和截尾分位数回归模型(CRQ)，最后计算出这1000个样本的回归系数的均数和标准差。模拟结果见表1。

表格中出现缺项的原因是因为随着截尾比例的不断增加，越来越多的截尾生存时间会随机地出现在生存时间分布的上游，直到观察结束时，生存率未降到0，即生存分布不完全，无法估计高分位数水平对应的回归方程。

模拟结果显示:对满足比例风险假定和对数线性假定的数据，Cox比例风险回归模型和截尾分位数回归模型拟合的回归系数与真值1非常接近，估计效率也相似。由于资料中不存在异质问题，所以不同分位数水平对应的回归系数非常接近。随着截尾比例的不断增加，回归系数可能会偏离真值1，估计的效率逐渐降低。该数据模拟实际上符合指数回归模型，采用加速失效时间模型估计的回归系数与真值1最接近，标准差最小，效率最高。

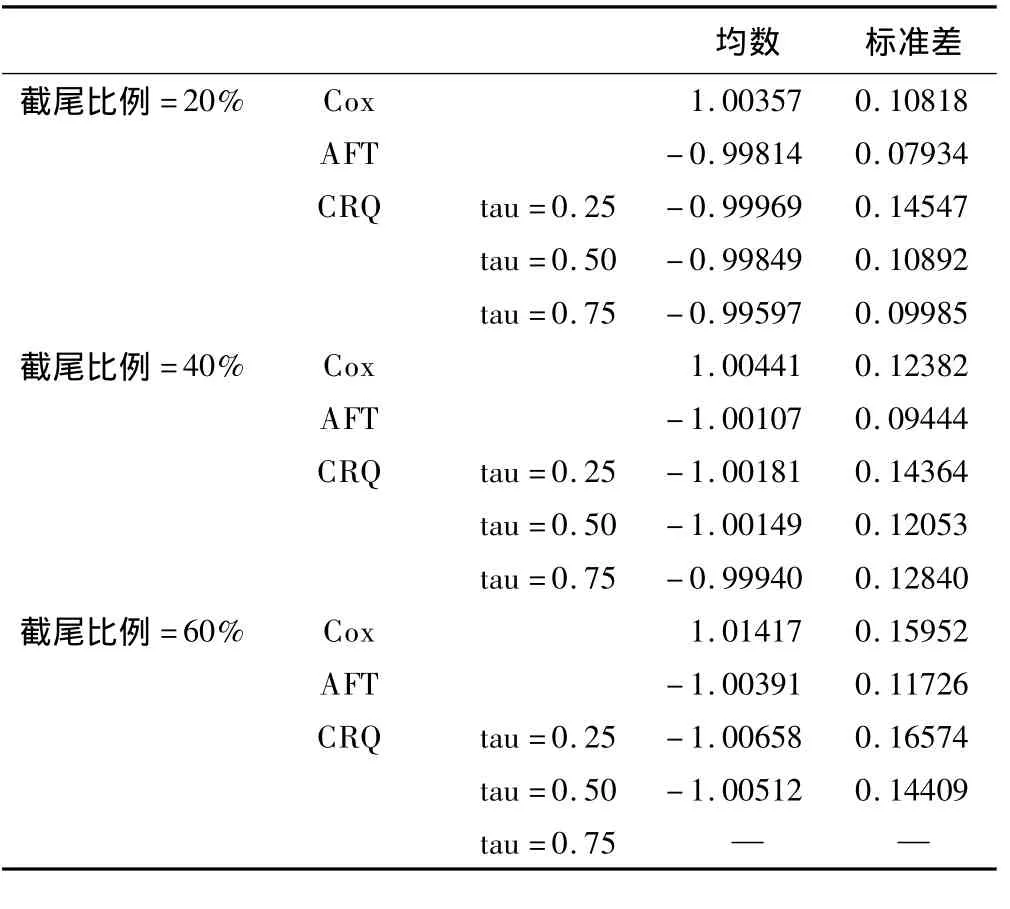
表1 不同截尾比例下回归系数的模拟分析

2．参数条件下存在离群点的模拟分析

模拟方法如下:模拟的样本含量为200，模拟的截尾比例分别为20%，40%，60%，模拟的离群点比例为5%，10%，15%，20%。首先产生服从(0.5，1.5)均匀分布的随机数作为自变量，再产生服从W(1，1)的威布尔分布随机数作为误差项，产生服从B(200，0.2)的随机数作为截尾指示变量，这时截尾比例为20%。如拟定的模型是无离群点模型，利用log t=1+βx+ε(令β=1)便可以得到相应的对数生存时间log t。如拟定的模型是有离群点模型，离群点比例为5%，先从200例中随机抽取5%的对数生存时间数据，被抽中的对数生存时间数值在原值的基础上加5，作为离群点的对数生存时间，而原样本中其他个体的对数生存时间保持不变。由此构造离群点比例为5%的有离群点样本。每次得到1000个模拟样本，分别采用Cox比例风险回归模型(Cox)、加速失效时间模型(AFT)以及截尾分位数回归模型(CRQ)，最后计算出这1000个样本的回归系数的均数和标准差。模拟结果见表2～4。

表2 不同比例离群点下回归系数的模拟比较(截尾比例=20%)

表3 不同比例离群点下回归系数的模拟比较(截尾比例=40%)

模拟结果表明，当离群点存在时，Cox比例风险回归模型拟合的回归系数明显偏离真值1，出现了偏性，并且随着离群点比例不断增加，偏性越明显。当截尾比例较低(≤40%)时，截尾分位数回归模型(τ=0.5)拟合的回归系数较加速失效时间模型接近真值1，效率也比较高。但是截尾比例继续增加时，截尾分位数回归(τ=0.5)拟合的回归系数偏性比加速失效时间模型大，标准差也偏大，这是因为随着截尾比例的增加，就容易在生存分布的上游出现一定比例的截尾，从而造成了在较高水平的分位数函数估计有偏，效率也降低，但是在低水平的分位数函数拟合良好。

表4 不同比例离群点下回归系数的模拟比较(截尾比例=60%)

3．违背比例风险假定的模拟分析

有理论表明〔4〕，在参数加速失效时间模型家族中，只有威布尔回归模型(包括指数分布)既属于加速失效时间模型，又属于比例风险模型。对数正态回归模型和对数logistic回归模型不满足比例风险假定。此次模拟采用对数正态回归模型来产生数据。

模拟方法如下:模拟的样本含量为200，模拟的截尾比例分别为20%，40%，60%。首先产生服从(0，1)均匀分布的随机数作为自变量x，再产生服从N(0，1)正态分布的随机数作为误差项ε，产生服从B(200，0.2)的随机数作为截尾指示变量，这时截尾比例为20%。利用t=exp(1+βx+ε)(令β=1)便可以得到相应的生存时间t。每次得到1000个模拟样本，分别采用Cox比例风险回归模型(Cox)、截尾分位数回归模型(CRQ)，最后计算出这1000个样本的回归系数的均数和标准差。模拟结果如下(在模拟结果中，考虑到两模型中的回归系数不具有可比性，便将Cox模型中的回归系数按式QCox(τ|x)=H－10(－log(1－τ)exp(－x'iβ))进行了转换，表5中列出的就是转换后的结果)。模拟结果见表5。

模拟结果表明，Cox估计的回归系数有偏;CRQ拟合的结果接近真值1，且效率相比Cox模型偏高。随着截尾比例的不断增加，CRQ估计的效率有下降的趋势。

实例分析

导尿及留置导尿管是临床上诊断、治疗各种危重病人的常用护理措施之一，但长期留置导尿管的多数病人会不同程度地出现导尿管引流不畅及尿液从导尿管渗漏等问题，且并发症较多，其中最严重的是尿路感染。因此寻找尿管诱发尿路感染的影响因素是我们迫切需要解决的问题，从而为预防感染提供一定的科学依据。

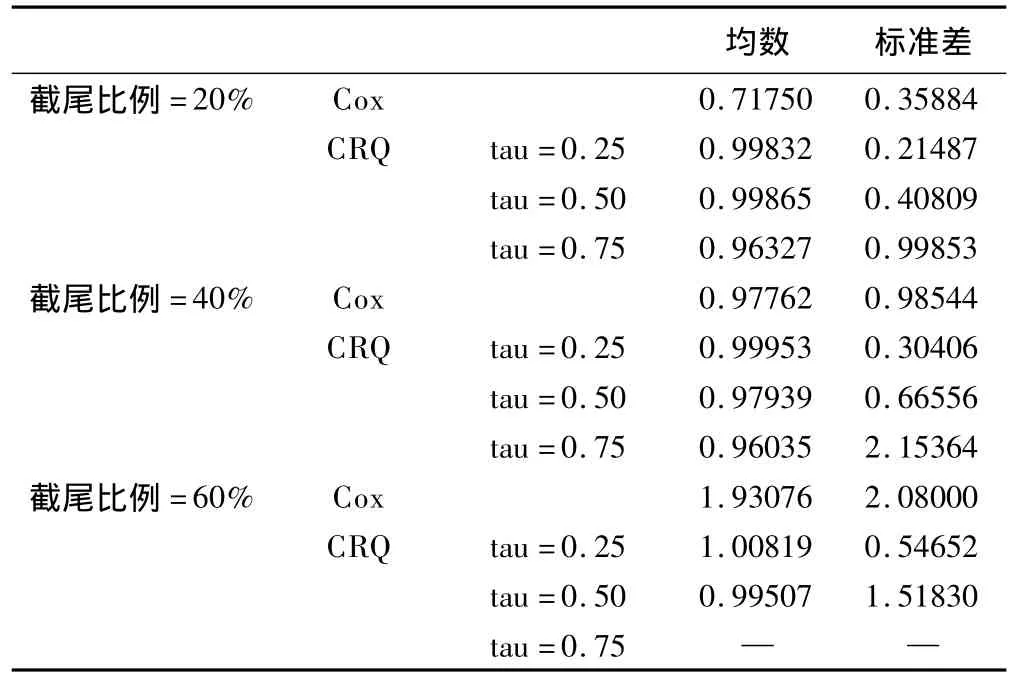
表5 不同截尾比例下回归系数的模拟分析

某医院泌尿外科的临床医师搜集了76例配备有便携式透析设备的肾衰病人。记录了这些病人从开始插入导管到感染的时间(以天计算)，如果直到研究结束仍未出现感染，或因为某些原因(感染除外)中途移除导管的病人，视为截尾。随访结束时，共有58例患者出现了感染。此外，还搜集了病人的年龄、性别、疾病类型以及衰弱评分四项指标。这四项指标的赋值情况和基本统计表见表6。利用76例肾衰病人拟合截尾分位数回归模型，在

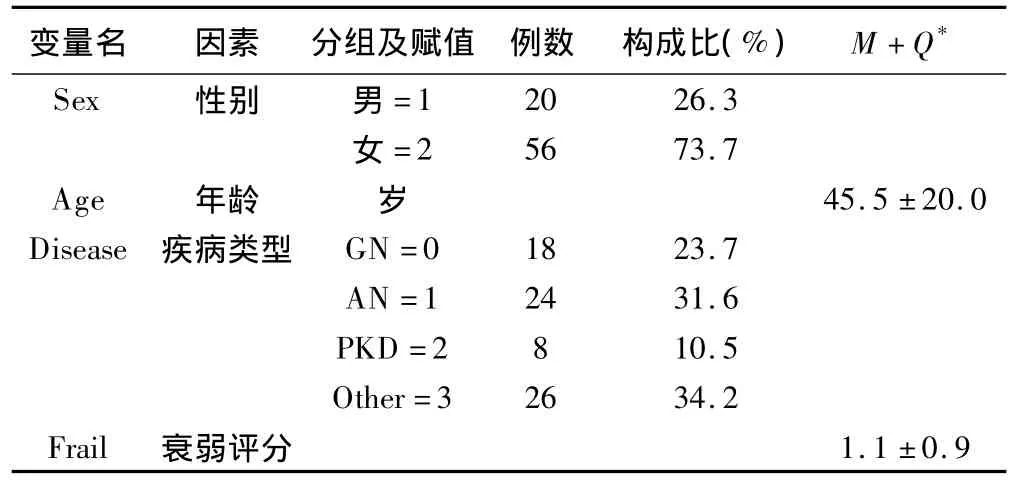
表6 76例肾衰病人生存资料预后因素及其基本统计量

α=0.10水平上，利用手动向后筛选变量法，入选的变量为性别(sex)、疾病类型GN(disease GN)、疾病类型

AN(disease AN)、疾病类型PKD(disease PKD)以及衰弱评分(frail)，交互项均无意义。模型拟合结果显示在不同的分位数函数上不仅表现为影响变量个数的不同，还表现为相同自变量对应的回归系数值大小不等。这里，只列举τ=0.1，0.5，0.9三个分位数水平对应的回归方程。

log t0．1=8.91 －2.73GN －2.273AN+32.183PKD

log t0．5=54.06 －98.35sex －5GN － 69.87AN +15.90PKD－81.61frail

log t0．9=373.24 －96.81GN －141.49AN+156.70PKD－176.82frail

从图1可以看出性别对log t影响的回归系数随着τ的变化而变化(先增加后下降)，疾病类型AN(以other为参考)对log t影响的回归系数的绝对值随着τ的增加而增加，衰弱评分对log t影响回归系数的绝对值随着τ的增加而增加。即随着生存时间的增加，说明性别对生存时间的保护作用先逐渐增强后又逐渐减弱，疾病类型AN(以other为参考)和衰弱评分对生存时间的威胁性越来越强。而从Cox模型拟合的效果来看，各回归系数几乎不随τ变化，低估了性别、疾病类型AN和衰弱评分对生存时间的影响作用。从专业角度看，截尾分位数回归拟合的结果更接近实际情况。

讨 论

在生存分析中，截尾分位数回归模型一般用于如下情况:(1)当数据有离群值，为削弱其对回归模型的影响;(2)当y的方差不是常数方差，即存在异方差，或者存在其他类型的异质性问题。此时，用中位数回归模型估计给定x时y的平均水平(中位数)，用其他分位数回归模型估计相应的容许区间或参考值范围。截尾分位数回归模型的特性亦类似于百分位数。如在截尾分位数回归中，中位数回归模型较其他百分位数回归模型稳定，越是接近0%和100%的百分位数回归模型越易受离群值和截尾值的影响，越是不稳定。因此，在用截尾分位数回归模型确定y的容许区间时，宜用70%，80%或90%的区间，而不用95%，98%或99%的区间〔5〕。

截尾分位数回归模型中，回归系数向量中^β(τ)第j个元素表示的是固定其他协变量时第j个协变量的单位变化引起第τ分位数的平均变化量。如果在线性截尾分位数回归模型中只表现为截距项的不等，即位置的漂移，而协变量对应的回归系数不随着τ变化，说明总体中不存在异质性;如果截尾分位数回归模型中协变量的回归系数随着τ变化，说明总体中存在异质性。因此，分位数回归模型不只可用来做多因素的统计分析，还能作为一种检验异质性的诊断方法。

1．Portnoy S．Censored regression quantiles．J．Amer．Statist．Assoc，2003，98:1001-1012．

2．Mara Tableman，Jong Sung Kim．Survival Analysis Using S:Analysis of Time-to-event Data．New York:Chapman ＆ Hall/CRC，2004．

3．余红梅．Cox比例风险回归模型诊断及预测有关问题的研究:〔博士学位论文〕西安:第四军医大学卫生统计学教研室，2001．

4．Kalblfeisch JD，Prentice RL．The Statistical Analysis of Failure Time Data．New York:Wiley，1980．

5．季莘，陈峰．百分位数回归及其应用．中国卫生统计，1998，15(6):9-11．