一种因果维纳滤波器的推导方法

吴素珍，焦计平，周又玲

（海南大学 信息科学技术学院，海南 海口 570228）

0 引言

20世纪40年代，维纳奠定了关于最佳滤波器研究的基础。即假定线性滤波器的输入为有用信号和噪声之和，两者均为广义平稳过程且知它们的二阶统计特性，维纳根据最小均方误差准则(滤波器的输出信号与需要信号之差的均方值最小)，求得了最佳线性滤波器的参数，这种滤波器被称为维纳滤波器。

在许多实际应用中，人们往往无法直接获得所需要的有用信号，能够观测到的一般是退化了或者失真了的有用信号。这就需要解决在噪声中如何提取信号的问题。维纳滤波就是用来解决这样一类从噪声中提取信号问题的一种过滤(或滤波)方法之一[1-3]。它是用线性滤波器实现对平稳随机过程的最佳线性估计。

随着计算机科学的发展,维纳滤波器在信号处理中得到越来越广泛的应用。继承维纳滤波器的思想，60年代，卡尔曼等人提出了卡尔曼滤波器，最后在维纳和卡尔曼的基础上，人们提出了自适应滤波器以及多方面的应用[4-5]。深刻理解维纳滤波器的数学原理,不仅对学习维纳滤波器是必要的,而且对全面系统地掌“数字信号处理”课程的基本概念、基本理论与基本方法也是十分重要的[6]。

1 维纳滤波器及维纳—霍夫方程

维纳滤波器是由数学家维纳提出的一种以最小均方为准则的线性滤波器，可以有效地从受污染的信号中提取有用信号。在一定的约束条件下，滤波器输出与期望输出的差的均方值达到最小。通过数学运算最终可变为一个托布利兹方程的求解问题。

维纳滤波器是实现对平稳随机过程的最佳线性估计。设计维纳滤波器的过程就是寻求在最小均方误差下滤波器的单位冲激响应h(n)或传递函数H(z)的表达式，其实质是解维纳-霍夫方程。

一个线性系统，如果它的冲激响应为h(n)，当输入一个随机信号x(n)，且：

其中s(n)表示信号，v(n)表示噪声。则输出 y(n)=sˆ(n)，则有：

模型如图1所示。

图1 维纳滤波器信号模型

式中，e(n)表示估计误差，定义为：

其中：

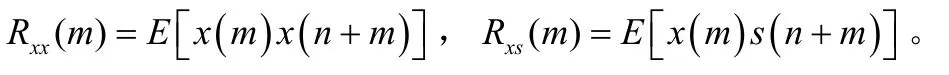
式（5）常称为维纳滤波器的标准方程或维纳-霍夫方程[7]。对于因果IIR维纳滤波器，其标准方程为：

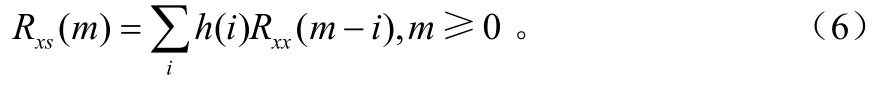
对于维纳-霍夫方程的求解，可以从时域进行求解，也可以从频域进行求解。由于有了m≥0的约束，时域求解该方程是困难的。所以往往转为频域和复频域求解。为此，博特和香农相继提出的将x(n)加以白化的方法来确定维纳-霍夫方程的z域解[8]。

假设信号s(n)和噪声v(n)都是平稳的，因此，滤波器的输入x(n)也是平稳随机信号，并可被看成由白噪声ε(n)激励一个线性移不变系统B(z)产生的输出。这里是有理函数，且N(z)和D(z)都对应于最小相位序列，故B(z)的全部零点和极点都在单位圆内。另一方面，若将x(n)作用于B(z)的逆系统，那么必将产生输出ε(n)，这就是对x(n)的所谓“白化”处理。就是把因果IIR维纳滤波器看成由两部分和G+(z)级联而成，这样，滤波过程包括两步，如图2给出这种方法的图示：第一步，用对x(n)进行白化处理，得到噪声ε(n)；第二步，用因果IIR维纳滤波器G+(z)对ε(n)进行滤波，得到最佳估计[7]。

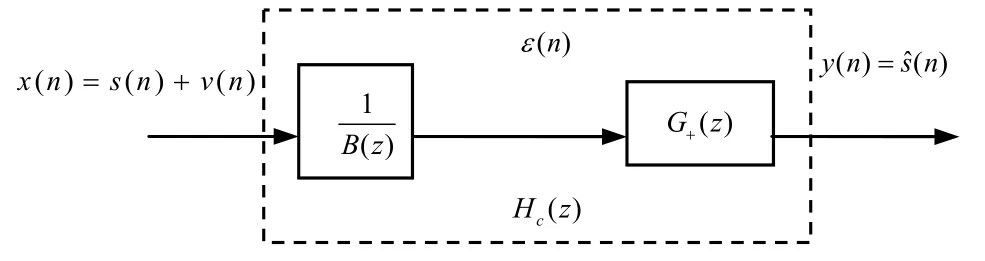
图2 将因果滤波器看成两部分级联

显然，待求的因果维纳滤波器的传输函数为：

经过推导，最终得到：

具体的公式推导过程，在参考文献[7]中可找到，此处从略。下面，笔者利用数字信号处理中Z变换性质，从另外一个角度，推导因果维纳滤波器的H(z)。

2 从单边Z变换推导法因果维纳滤波器的H(z)

[9-10]可知，序列x(n)，n∈Z的单边 z变换为：

由于维纳滤波器为满足维纳－霍夫方程的滤波器，即：

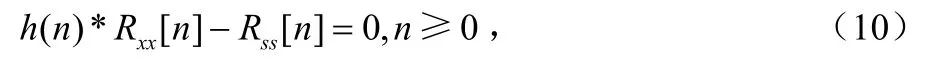
式中，“*”表示卷积运算。对式（10）两边同时取单边 z变换，可得：

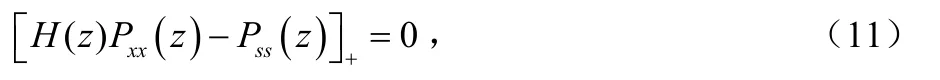
式中，

根据频谱因式分解定理可知，若Pxx(z)在单位圆上无零点，那么：

式中，B(z)是因果序列的Z变换，而B(z−1)为非因果序列的Z变换，在大多数情况下，Pxx(z)是满足该条件的。对于单边Z变换而言，可以推证其如下性质：

性质1 若定义序列x(n)单边及因果Z变换为：

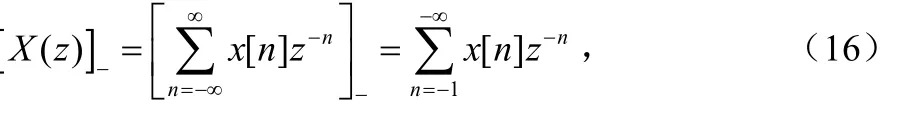
则：

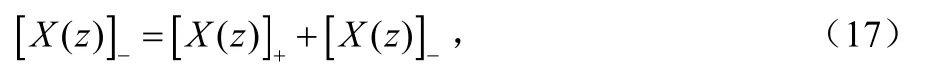
进一步地，由式（9）、式（17）可知：

性质2 若：

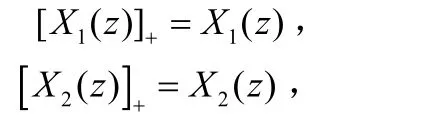
即x1(n), x2(n)同为因果序列。由此可知 x(n)=x1(n)∗x2(n)亦为因果序列。因此[X(z)]+=X(z)=X1(z) X2(z)，式中，X(z)=Z[x(n)]，为序列x(n)的Z变换。

由式（3）可以分解为：

其中H(z)为因果序列h(n)的子变换，B(z)也为因果序列的Z变换，因此：

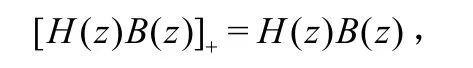
由此可知：

3 实例

4 结语

在因果维纳滤波器的推导算法中，式（18）和式（19）对整个推导过程是至关重要的。从式（20）可以看出，利用这里所述的方法得到的因果滤波器与其他方法得到的结果是一致的，这说明该算法的正确性。另外，这里所提到的算法和其它算法的不同之处在于求解过程主要基于数字信号处理中Z变换性质，属因果维纳滤波器的一种较为新颖的推导方法。

参考文献

[1] 陈乃金.周鸣争.潘冬冬.一种新的维纳滤波图像去高斯噪声算法[J].计算机系统应用,2010,19(03):111-114.

[2] 巴万宏,谢显中.维纳滤波在 TD-SCDMA 下行链路中的研究[J].通信技术,2007,40(09):21-22.

[3] 邵宁,陈万培,陈俊晟.一种基于维纳滤波器抗 MAI 的新方法[J].通信技术,2010,43(05):224-226.

[4] 唐建锋,张登玉,罗湘南.一种基于多尺度小波变换的自适应滤波新算法[J].通信技术,2008,41(12):405-407.

[5] 任晓亚，宋爱民.自适应算法在干扰抵消器应用中的比较研究[J].通信技术,2007,40(12):48-50.

[6] 张专成.因果维纳滤波器均方误差计算公式的简化[J].武警工程学院学报,2002(06):16-18.

[7] 姚天任，孙洪.现代数字信号处理[M].武汉科技大学出版社,1999:20.

[8] 崔晓杰.维纳滤波器的应用研究[D].陕西:长安大学,2006.

[9] 王世一.数字信号处理[M].北京:北京理工大学出版社,1997:54.

[10] 门爱东,杨波,全子一.数字信号处理教程[M].北京:人民邮电出版社,2003:58.