不确定水质模型在城市河流水质模拟中的应用

田一梅,刘 扬,王彬蔚,2

(1.天津大学环境科学与工程学院,天津 300072;2.陕西省环境监测中心站,西安,710054)

不确定水质模型在城市河流水质模拟中的应用

田一梅1,刘 扬1,王彬蔚1,2

(1.天津大学环境科学与工程学院,天津 300072;2.陕西省环境监测中心站,西安,710054)

鉴于城市景观河流受沿河排水污染,水质波动较大,建立了内嵌神经网络的一维不确定性水质模型,利用改进适应度函数的遗传算法,优化水质模型的参数解。经实例验证,不确定性水质模型拟合的精度更高,对排入污染物的波动更敏感,其对景观河流水质预测的平均准确度基本在80%以上,普遍高于确定性水质模型,尤其是在靠近污染源的监测断面,其不确定性水质模型预测优势更加明显,更能适应变化的景观河流水体环境。

不确定性水质模型;人工神经网络;遗传算法;模拟

水质模型是用来描述水体中污染物与时间、空间的定量关系,描述物质在水环境中的混合、迁移过程的数学方程。根据模型中的变量是否为随机变量,水质模型可分为确定性水质模型和不确定性水质模型。确定性水质模型,如 SIMCAT, TOMCAT,QUAL2E,QUASAR,MIKE-11和ISIS[1-2]等已广泛应用于水环境的模拟预测,但由于水环境的不确定性、复杂性,使水质变化呈现出基于一定变化规律的不确定性变化特征,同时由于监测数据本身均带有随机性,故建立不确定性水质模型更能反映水质的实际变化规律[3]。

早年的不确定性水质模型较多是利用随机理论建立的,如1966年Loucks和 Lgnn基于随机过程理论首先提出了预测最小溶解氧的概率模型,1969年Custer与K rutcheff[4]提出了随机游动模型,1984年,Deway提出了BOD-NOD-DO随机模型。而近年来,随着神经网络理论的成熟,将其应用于各类不确定性水质模拟问题已逐渐成为重要的研究方向之一,2002年Huang和Foo[5]利用人工神经网络模拟了受支流流入、潮汐以及风力等不确定性因素影响的河流中盐度的变化;Maier等人[6]利用人工神经网络对混凝剂的投加量进行了优化;Mozejko等人[7]和Chen等人[8]模拟了河流中氮磷浓度的变化;利用人工神经网络模拟可以增强处理非线性问题的能力,使得水质预测精度得以提高。一般来说,由于人工神经网络算法局部精确搜索的特性,容易陷入局部最优,故对于波动性较大的数据,易导致过拟合而影响预测精度,利用全局搜索的遗传算法与之结合,能够有效的摆脱局部极点的困扰[9]。以北方某工业园区J河为研究对象,通过监测、分析该河主要污染物指标的变化,研究沿河排水对河流水质的影响,利用内嵌神经网络建立了一维不确定水质模型,利用遗传算法求解模型参数,提高了对城市河流水质模拟预测的精度。

1 一维不确定性水质模型的建立

J河部分为天然河道、部分经人工开挖,所处区域地势平坦,地面坡度小于1/1 000,河水流速缓慢。河平均宽度30 m,平均水深2.2 m,河长约13 km。其水源主要为附近河网来水及该区域径流雨水。经监测上游来水及沿河排水中部分指标经常不满足地表水Ⅴ类标准,且波动较大,并影响了J河水质。

由于J河的宽度、深度与其长度相比较小,河流的竖向与横向均匀混合所需的距离远远小于J河的河长,因此可假设污染物在河流的横断面上瞬时达到均匀混合,故采用一维水质模型即可取得很好的近似。

利用一维水质模型预测CODCr和氨氮的变化,以CODCr为例,当考虑纵向弥散条件时,一维水质模型的方程为：

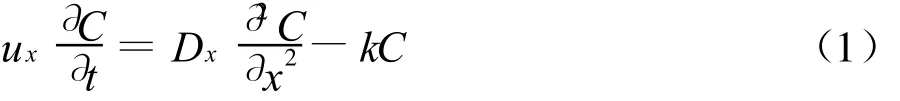
式中：C为河段中某污染物质的浓度,mg/L;ux为河流的流速,m/s;x为距污染源排放断面的距离, m;k为污染物降解系数,d-1;D x为河流的纵向弥散系数,m2/s。

J河的纵向弥散系数可利用矩阵法[10]求得,结果如表 1所示,k值可利用 MATLAB中的Fminsearch函数拟合得到,为0.095 2d-1。

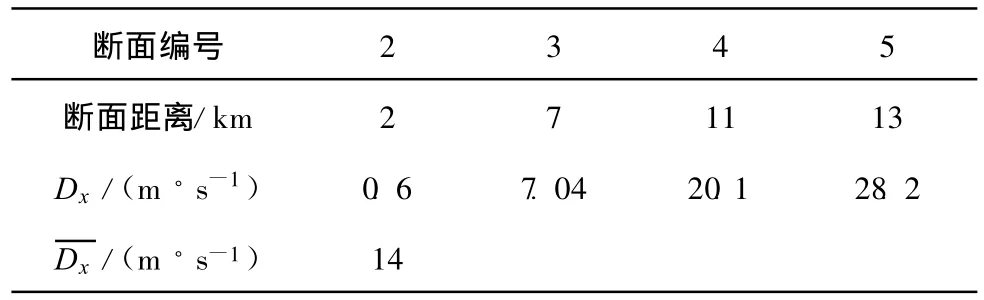
表1 J河各断面处纵向弥散系数

当不考虑弥散条件时,一维水质模型方程如(2)式所示,拟合得到的k值为0.095 1 d-1：

图1所示的上述两种条件下拟合出的不同时刻各断面处CODCr浓度结果十分相近,因此为了简化一维模型,可忽略J河的纵向弥散作用。图1显示确定性一维水质模型对J河中污染物降解的拟合效果不理想,估计与沿河排水的水质波动有关,因此在忽略河流弥散作用的一维模型中增加一项对排水水质的波动的观测变量,建立了一维不确定水质模型,见式(3)。

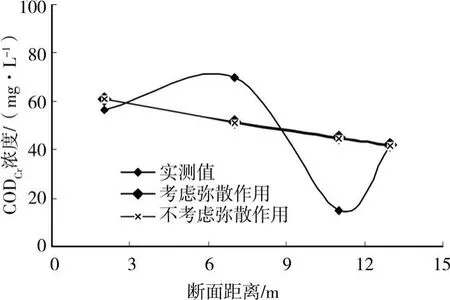
图1 各断面的CODCr监测值与一维确定性水质模型预测值的比较

式中：U为水质变化不确定因素影响的外部观测量,可以是一个变量,也可以是一个函数。

式(3)建立的关键在于U与模型参数的合理确定。

1.1 不确定因素表征

水环境是一个充满不确定因素的复杂系统,其不确定性主要来源于污染物排放量与河流水文条件的不确定性、由于对水环境中复杂的物理生化反应机理认知不足造成的水质模型结构的不确定性、水质模型参数确定所需的河流及水质资料的不确定性、未观察到的模型输入过程中各种扰动所造成的不确定性[11]等等。其中有些不确定因素是可以通过一定时间内的水质监测数据反映其主要变化信息。而神经网络是以数据为基础,通过对系统历史数据的学习训练来掌握系统内部的变化规律,无需构建模型,同时,神经网络应用简便,具有较强的自适应性,非常适合于处理具有不确定性和非线性的水环境问题。

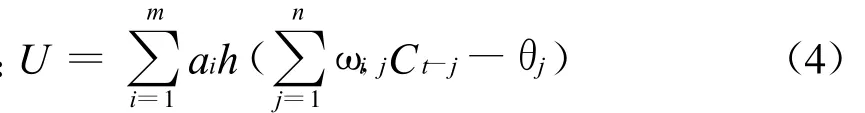
1.2 不确定性水质模型建立

式(4)所构建的神经网络函数是以连续若干天污染物输入断面的水质监测数据作为网络的输入元,通过对一段时间内网络数据的学习、训练,感知污染物随机排放量的变化,从而建立一个具有学习功能的不确定性水质模型,见式(5)：

式中：Ct为t时刻河段中某污染物质的浓度,m g/L;

根据景观河监测数据分析及网络建模试算,选取CODCr、NH3-N作为建模指标,取污染物输入断面(1-1断面)4 d的水质监测数据作为模型训练的样本,则网络输入层节点数为4,其相应隐层节点数采用Hecht-Nielsen的“2N+1”法确定为9,经解式(5)可得不确定性水质模型为：

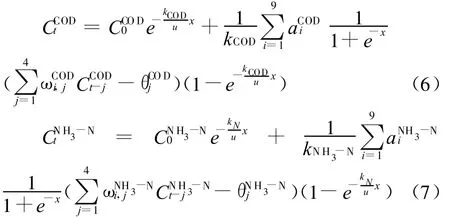
2 不确定水质模型参数估计

式(5)显示,不确定水质模型中待估参数除污染物衰减系数k之外,还增加了网络参数、并构成一个多参数寻优问题,其目标函数可取为污染物模型计算值与实测值的绝对百分比误差之和：

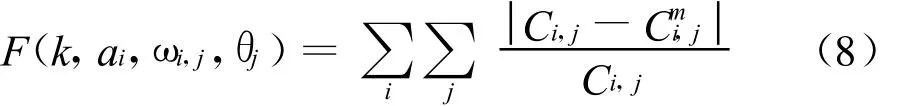
ij

由于模型参数的合理确定,将影响到内嵌的神经网络函数与传统的水质模型能否形成一个有机整体,可否提高对各种不确定因素带来的水环境时空变化的预测水平,因此,选择适当的解法至关重要。根据遗传算法有利于在不确定的环境中寻找最优控制解[12],选择改进适应度函数的遗传算法[13-16],利用景观河水质监测数据,对不确定水质模型参数进行求解。

2.1 适应度函数

基于遗传算法在运行早期时,初始群体中可能存在特殊个体的适应度值超常现象,为了防止其统治整个群体并误导群体的发展方向而使算法收敛于局部最优解,即遗传算法的早熟现象,本文采用Goldberg[17]提出的线性变化适应度拉伸法构造适应度函数,使种群个体适应度成等差数列均匀分布,从而避免早熟和停滞问题,并加快函数的收敛速度,减少起始收敛代数。线性适应度函数如式(9)所示：

2.2 模型参数求解

利用MATLAB编写遗传算法程序确定水质模型参数,模型计算所需参数设置：交叉概率= 0.2,变异概率=0.2,各待估参数的取值范围：根据景观河监测数据试算,其CODCr、NH 3-N衰减系数均小于0.5,故令,同时,选择ai,ωij,θj∈(-100,100),先在此范围内搜索最佳适应度,若最佳适应度未能小于0.5,需进一步放大ai,ωi,j,θj取值范围,直至最佳适应度小于0.5为止。表2、表3为COD Cr、NH3-N不确定性水质模型式(6)、式(7)的参数估计结果。

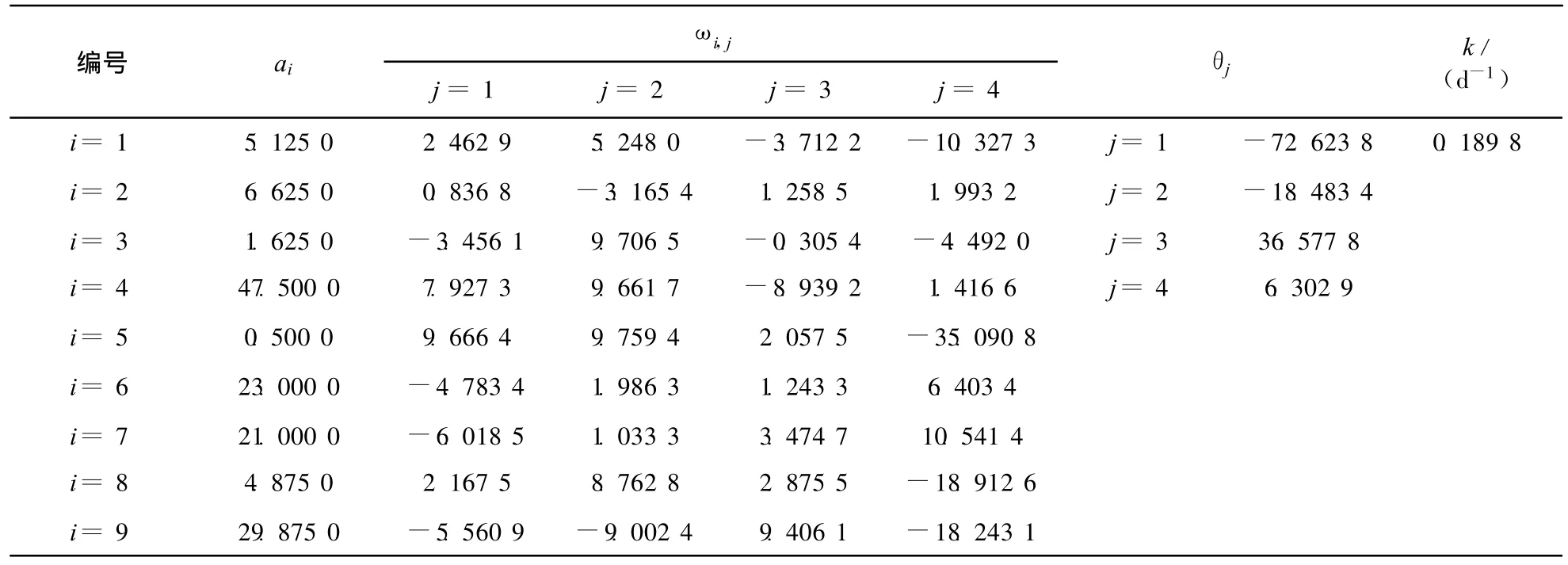
表2 CODCr不确定性水质模型参数估计

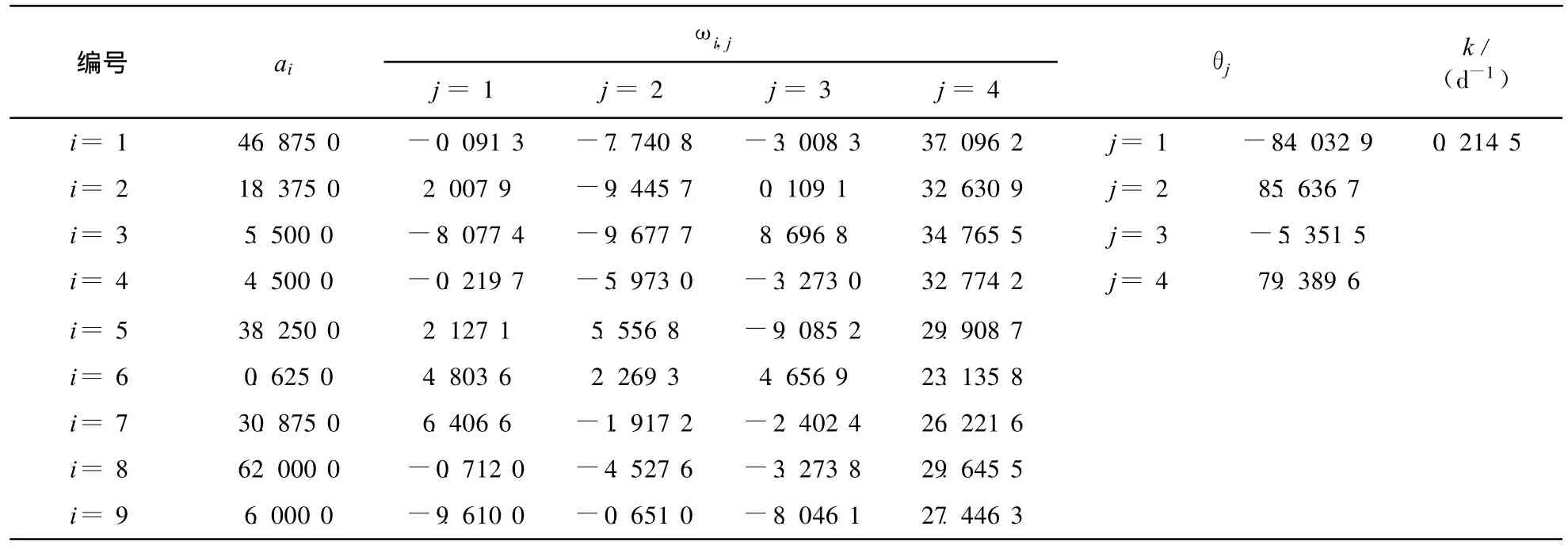
表3 NH 3-N不确定性水质模型参数估计

3模型预测结果分析比较

3.1模型预测结果

利用上述建立的不确定性水质模型,对景观河7月下半月4个断面的CODCr、NH 3-N值进行预测。预测时网络的输入数据随预测日的变化而向前推移,即总是选取预测日前4 d的污染物输入断面的监测数据。此外,为比较不确定性水质模型预测效果,采用相同监测数据,建立了确定性水质模型(公式略),并分别对各断面的CODCr、NH3-N进行预测,图2、图3为河流2-2断面的预测结果。

表4为确定性水质模型与不确定性水质模型的部分计算参数和预测平均误差的对比。

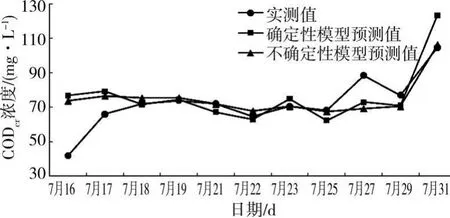
图2 2-2断面的CODCr监测值与预测值

图3 2-2断面的NH3-N监测值与预测值

表4 两种水质模型部分计算参数和预测平均误差对比

分析表4可知：

1)不确定性模型给出的污染物衰减系数均小于确定性模型的相应系数,说明增加了神经网络观测项,对污染物衰减规律有所调整。

2)两类模型的目标值(适应度函数值)不同,说明不确定性水质模型拟合的精度更高,更能适应变化的景观河水体环境。

3)从预测效果分析,不确定性水质模型的预测平均水平均高于确定性水质模型,平均预测误差减小幅度达0.24%～15.90%,预测精度基本在80%以上,尤其是在靠近污染物输入断面的2-2断面,预测精度明显高于其它下游断面,说明增加的神经网络函数对排水水质的波动是比较敏感的,而其他下游各断面虽然预测精度也有提高,但因距污染物输入断面距离逐渐加大,其水质变化将会受到更多的其他随机因素的扰动。

4)当然,不确定性水质模型的预测结果中仍有部分预测误差大于确定性水质模型的预测,其中CODcr占41%,NH3-N占33.33%,但其误差增幅不大;而且所有预测结果中对CODcr的预测误差超过30%的仅为11.36%,对NH3-N的预测误差超过30%的也只有16.66%,基本满足日常水质管理的需要。

4 结 语

针对排入景观河水体的排水水质的不确定性,本文建立内嵌神经网络的一维不确定性水质模型,利用改进适应度函数的遗传算法,获得模型参数的最优解。经模型计算参数及预测结果的比较分析,不确定性水质模型拟合的精度更高,更能适应变化的景观河水体环境,其预测平均水平普遍高于确定性水质模型,且靠近污染源的监测断面,其不确定性水质模型预测优势更加明显。

[1]COX B A.A review of currently available in-stream waterquality models and their app licability for simu lating dissolved oxygen in low land rivers[J].Science of the Total Environment,2003,314：335-377.

[2]FANG X B,ZHANG JX,CHEN Y X,et al.QUAL2K model used in the w ater quality assessment of qiantang river,China[J].W ater Environment Research,2008,80 (11)：2125-2133.

[3]许劲,龙腾锐.不确定性河流水质模型的应用及进展[J].中国给水排水,2007,23(16)：4-8.

XU JIN,LONG TENG-RU I.App lication and Progress of uncertainty river w ater quality mode l[J].China Water&Wastew ater,2007,23(16)：4-8.

[4]KARMAKARA S,MUJUMDAR P P,An inexact optimization app roach for river water-quality management [J].Journal of EnvironmentalManagement,2006,81(3)：233-248.

[5]HUANG W R,FOO S.Neural network modeling of salinity variation in Apalachicola river[J].Water Research,2002,36(1)：356-362.

[6]MA IER H R,CHOW C W.Use of artificial neural netw orks for predicting optimal alum doses and treated water quality parameters[J].Environmental Modelling &Sof tw are,2004,19(5)：485-494.

[7]MOZEJKO J,GNIOT R.A pp lication of neural networks for the prediction of total phosphorus concentrations in surface w aters[J].Polish Journal of Environmental Studies,2008,17(3)：363-368.

[8]CH EN D J,LU J,SHEN Y N.A rtificial neural netw ork modelling of concentrations of nitrogen, phosphorus and dissolved oxygen in a non-point source po lluted river in Zhejiang province,southeast China[J]. Hyd rologica l Processes,2009,24：290-299.

[9]翟宜峰,李鸿雁,刘寒冰,等.用遗传算法优化神经网络初始权重的方法[J].吉林大学学报：工学版,2003,33 (2)：45-50.

ZHA IYI-FENG,LIHONG-YAN,LIU HAN-BING,et al.Method for optimizing initial w eights of ANNs by GAs[J].Journal of Jinlin University：Engineering and Technology Edition,2003,33(2)：45-50.

[10]程声通,陈毓龄.环境系统分析[M].北京：高等教育出版社,1990.

[11]李如忠.河流水环境系统不确定性问题研究[D].南京：河海大学环境科学与工程学院,2004.

[12]CHEN H W,CHANG N B.W ater pollution control in the river basin by fuzzy genetic algorithm-based mu ltiob jective p rogramm ingmodeling[J].W ater Science and Technology,1998,37(8)：55-68.

[13]刘臣辉,刘超,徐香,等.基于改进遗传算法率定水质参数的研究[J].环境保护科学,2008,34(3)：47-49.

LIU CHEN-HUI,LIU CHAO,XU XIANG,et al. Parameter estimation of water quality model based on imp roved genetic algorithm [J].Environmental Protection Science,2008,34(3)：47-49.

[14]闫欣荣,史忠科.反演-遗传算法在河流水质BOD-DO藕合模型参数识别中的应用[J].水资源与水工程学报, 2007,18(4)：41-43.

YAN XIN-RONG,SH I ZHONG-KE.Application of Inversion-Genetic algorithms to parametersidentification for the BOD-DO water quality coup ling model[J].Journal of Water Resources and Water Engineering,2007,18(4)：41-43.

[15]梁婕,曾光明,郭生练,等.变尺度混沌-遗传算法在复杂河流水质模型参数优化中的应用[J].环境科学学报, 2007,27(2)：342-347.

LIANG JIE,ZENG GUANG-MING,GUO SHENGLIAN,et al.Application of mutative scale chaos genetic algorithm(MSCGA)to parameters estimation for river w ater quality model[J].Acta Scientiae Circumstantiae, 2007,27(2)：342-347.

[16]王建平,程声通,贾海峰.基于MCMC法的水质模型参数不确定性研究[J].环境科学,2006,27(1)：24-30.

WANG JIAN-PING,CHEN SHENG-TONG,JIA HA IFENG.Markov Chain monte carlo scheme for parameter uncertainty analysis in w ater quality model [J].Environmental Science,2006,27(1)：24-30.

[17]GOLDBERG D E.Genetic algorithm s in search, op tim ization and machine learning[M].United States：Addison W esley Pub lishing,1989.

(编辑 胡 玲)

App lication of Uncertain Model in Urban River Quality Simu lation

TIANYi-mei1,LIUYang1,WANGBin-wei1,2

(1.Schoolof Environmental Science and Engineering,Tian jin University,Tianjin 300072,P.R.China; 2.Shanghai EnvironmentalMonitoring Center of Shanxi Province,Xian 710054,P.R.China)

Ow ing to the fluctuation of water quality in urban river which polluted by drainage along river, one-dimension uncertain water quality model embeded neural network is established.Genetic algorithms and am odified fitness function are used to optimize parameters of the uncertain model.Examp les illustrate that the uncertainmodel has higher prediction accuracy w ith the average accuracy over80%than the certain model,and ismore sensitive to the fluctuation of pollutants discharged into the river.The uncertain model has a significant advantage of prediction and could better adapt to the changing urban water environment, especially at points close to the po llution sources.

uncertain water quality model;artificialneural network;genetic algorithm s;simulation

X 522

A

1674-4764(2011)03-0119-05

2010-03-10

国家水体污染控制与治理重大专项(2008ZX07314-003);天津市科技创新专项资金资助项目(O 6FZZDSH 0090)

田一梅(1959-),女,教授,博士,主要从事环境系统优化研究,(E-mail)ym tian_2000@yahoo.com.cn