机械结构因素对谐振腔无载Q值的影响分析
熊长武
(中国西南电子技术研究所,成都 610036)
机械谐振腔是现代通信和雷达等工程应用领域中一种常用的微波器件,其无载Q值(品质因素)是表征谐振器频率选择性的优劣和能量损耗程度的基本参量[1]。对于理想模型,谐振腔几何形状、尺寸、材料等机械结构因素对无载Q值的影响关系前人已作了大量的研究并已趋成熟。而工程中常见的机械谐振腔总是由多个零部件拼装而成,其腔体不同组件表面、组件接缝处的机械、电气特性与理想模型均有明显差异,从而导致工程产品的理论计算结果与实测值存在较大的误差。解决该问题的思路是在传统计算模型的基础上增加工程实际的机械结构影响因素,同时考虑不同部位结构因素影响无载Q值的差异,从而消除理想模型与工程模型间的计算误差。
1 同轴谐振腔机械结构特征及中间电参量
1.1 同轴谐振腔机械结构特征
机械谐振空腔实质是一段两端短路的波导传输线,而同轴谐振腔实质就是一段单端短路的同轴传输线,如图1所示。
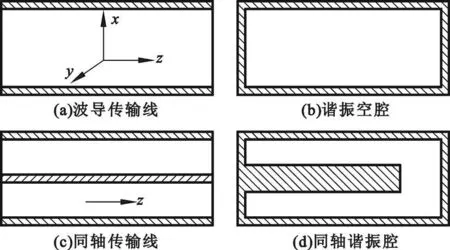
图1 同轴谐振腔结构特征Fig.1 Structure character of coaxial resonant cavity
按同轴谐振腔组成部件的一般定义[2],将外形空腔称作谐振腔,将一端短路的同轴内导体称作谐振器,两者共同决定谐振腔的品质因数及频率选择特性。工程上典型的同轴谐振腔分为矩形同轴谐振腔和圆形同轴谐振腔两种,当同轴谐振腔作为机械滤波器等微波器件的重要组成部件时其详细结构还要复杂得多,包括耦合孔、耦合环、调谐膜片、螺钉等,结构形式如图2所示。从简化分析的角度出发本文只研究最简单的同轴谐振腔。
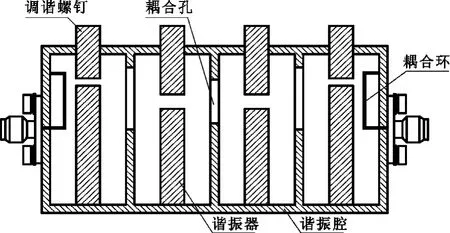
图2 四腔滤波器同轴谐振腔结构特征Fig.2 Structure character of four stepped-impedance resonators filter
1.2 影响无载Q值的机械结构因素
无载Q值表征的是谐振腔频率选择性的优劣和能量损耗的程度,其中频率选择性主要取决于谐振器腔体的几何形状、尺寸,能量损耗主要源于腔壁导体和腔内介质的损耗,与腔体及介质材料、表面特征、装配连接质量相关[3]。理想条件下圆形同轴谐振腔机械结构因素对无载Q值的影响关系如下:式中,Qu为腔体无载Q 值,ω0为角频率,μ0为材料磁导率,σ为材料电导率,l为腔体长度,a为腔体内半径,b为腔体外半径。

实际上,影响无载Q值的机械结构因素远不止这些。根据相关理论分析及工程实践可知,机械结构因素影响无载Q值的层次关系如图3所示。

图3 机械结构因素影响无载Q值的层次关系Fig.3 The hierarchy relationship between mechanical structure factor and unloaded Q value
由此可见,影响无载Q值的机械结构因素主要有3类,一是几何形状及尺寸偏差,二是材料加工质量所致的表面有效电导率偏差,三是装配连接质量引起的装配接触电阻偏差。而式(1)仅反映了机械结构尺寸、材料电导率、磁导率等基本参数对无载Q值的影响,没有考虑腔体表面射频有效电导率与材料电导率的差异以及腔体装连接配质量对无载Q值的影响,更没有对这些影响因素进行组件级的分解,而工程实际中这些参数往往对电性能指标造成非常大的影响。
1.3 机械结构因素与中间电参量的等效关系
由于上述影响无载Q值的机械结构因素无法直接反映到分析计算模型中,需要建立射频有效电导率及集中接触阻抗等中间电参量的方法将其等效反映到分析模型中。
1.3.1 射频有效电导率
在微波工程电路设计中,将实际导波表面所表现出的电导特性称为射频有效电导率[4]。根据微波表面理论,对于良导体,射频表面电流存在趋肤效应而被限于导体表面约3个趋肤深度的范围内流动,其在第一个趋肤深度范围内最集中,可达总电流的63.2%。频率越高趋肤深度越小,表面电流越集中,表面粗糙度及镀层质量对射频有效电导率的影响越明显。
在纯铜表面、6 GHz频率条件下,微波器件表面二维粗糙度(粗糙度Ra、轮廓长度率Rl)与射频有效电导率存在如图4所示的关系曲线[5]。

图4 二维粗糙度与有效电导率系数间的关系Fig.4 Relationship between planar roughness and RF equivalent conductivity coefficient
镀层质量对表面电导率的影响因素主要有镀层厚度、镀层纯度、镀层致密度、镀层表面粗糙度等。以表面镀银为例,当镀层厚度达到3~5倍趋肤时,根据工程数据分析及经验总结,镀层有效电导率一般相当于镀层材料直流电导率的80%~90%。
综合考虑上述各种影响即可得到谐振腔各部件表面的射频有效电导率如下:

式中,σ′为部件表面射频有效电导率,σ为材料直流电导率,αn为电导率有效系数。
1.3.2 集中接触阻抗
任何实际导体传输电波或电流都存在阻抗,阻抗分为实部阻抗和虚部阻抗、分布阻抗和集中阻抗,造成能量损失从而影响无载Q值的是实部阻抗。如用接缝处射频集中接触阻抗来区别其它表面的分布阻抗,则不同结构形式或装配连接质量影响无载Q值的实质是在同轴腔体不同组件间形成了附加的等效射频集中接触阻抗,该接触阻抗与同轴腔体表面电阻(分布阻抗)共同造成腔体内电磁能量的损失。腔体组件间接缝处的集中接触阻抗,在直流或低频频段时非常小,但在高频(厘米、毫米波频段)时会非常明显,严重影响腔体无载Q值。
目前还无法准确地计算某一装配连接质量、某一频率条件下集中接触阻抗的大小,只能通过样件测试、数据分析结合工程经验进行预估。
2 同轴谐振腔无载Q值仿真分析
2.1 同轴谐振腔仿真分析模型
根据谐振腔机械结构特征及影响无载Q值的机械结构因素分析,可将圆形同轴谐振腔分解为5个组件表面和3条组件间接缝,分别是腔顶面、腔侧面、腔底面、振子侧面、振子顶面、腔顶接缝、腔底接缝、振子接缝,如图5所示。利用HFSS电磁场仿真软件建立仿真分析几何模型,其中5个面与设计尺寸一致,3条接缝根据仿真模型的需要用狭窄面或薄片体代替。

图5 圆形同轴谐振腔仿真几何模型Fig.5 Simulation geometry model of circular coaxial resonant cavity
仿真分析几何模型建立完成后还需要赋予边界条件、物性参数等。在本文的研究工作中,首先是5个组件表面电导率不再采用材料的直流电导率,而是采用上节所述的表面射频有效电导率;其次是在3条组件间接缝替代面(或薄片)上赋予如上节所述的等效集中射频接触阻抗,一般是在材料物性参数上附加一个方阻系数来等效。方阻系数的取值与仿真几何模型密切相关,针对本文的研究案例,一般取接触处方阻系数为0.3 ohms/square(ohms/square为Ansoft软件中定义的单位)。
对于矩形同轴谐振腔,亦可建立类似的仿真分析几何模型,同时赋予等效的边界条件和物性参数,如图6所示。

图6 矩形同轴谐振腔仿真几何模型Fig.6 Simulation geometry model of rectangle coaxial resonant cavity
2.2 射频有效电导率对无载Q值的影响关系
首先分析圆形同轴谐振腔不同组件表面射频有效电导率对无载Q值的影响,以6GHz为中心频率、以纯铜为基准电导率,通过仿真分析及数据处理得到各面有效电导率系数与无载Q值的关系如图7所示。

图7 圆形同轴谐振腔电导率有效系数对无载Q值的影响关系Fig.7 The effect relationship between RF effective conductivity and unloaded Q value on circular coaxial resonant cavity
由图7可知,谐振腔各组件表面电导率有效系数对无载Q值的影响关系是不一致的,存在明显的差别,5个面的单因素影响汇总即为所有面的综合影响。当所有面的电导率有效系数接近于1时,其腔体无载Q值较高,随着各面电导率有效系数的减小,Q值也逐渐变小,但各个面影响的大小是不一样的。当电导率有效系数略为0.7时,5个组成面对无载Q值影响从大到小依次为振子侧面(-32.51%)、腔 底 面 (-22.42%)、腔 侧 面(-14.66%)、腔顶面(-2.0%)和振子顶面(-0.18%)。由此在满足电性能指标的前提下,为了获得较经济的生产成本和减小高精度加工的困难,可以适当提高对无载Q值影响较大的面的加工精度,降低对无载Q值影响较小的面的加工精度,从而进行各面加工精度的优化设计。
对于矩形同轴谐振腔,其电导率有效系数对无载Q值的影响关系如图8所示。

图8 矩形同轴谐振腔电导率有效系数对无载Q值的影响关系Fig.8 The effect relationship between RF effective conductivity and unloaded Q value on rectangle coaxial resonant cavity
2.3 集中接触阻抗对无载Q值的影响关系
接下来分析圆形同轴谐振腔不同位置接缝处集中接触阻抗对无载Q值的影响,同样以6 GHz中心频率、纯铜直流电导率为基准电导率,通过仿真分析及数据处理得到不同位置接缝处集中接触阻抗对无载Q值的影响关系如图9所示。

图9 圆形同轴谐振腔集中接触阻抗对无载Q值的影响关系Fig.9 The effect relationship between concentrated contact impedance and unloaded Q value on circular coaxial resonant cavity
由图9可知,谐振腔不同位置接缝处集中接触阻抗对无载Q值的影响关系是不一致的,存在明显的差别,3条接缝处的单因素影响汇总即为所有接缝的综合影响。当所有接缝的集中接触阻抗系数接近于0时,其腔体无载Q值较高,随着各处集中接触阻抗系数的增加,Q值也逐渐变小,但各处影响的大小是不一样的。当接缝处集中接触阻抗系数略为1时,3个接缝对无载Q值影响从大到小依次为振子接缝(-67%)、腔底接逢(-42%)、腔顶接逢(-5%)。所以,在满足电性能指标的前提下,为了获得较经济的生产成本和减小高精度加工的困难,可以适当提高对无载Q值影响较大的接逢处的装配连接质量,而降低对无载Q值影响较小的接缝的装配连接质量,从而进行组件结构的优化设计。
3 多因素影响权重模型
根据上节分析结果,对于圆形同轴谐振腔射频有效电导率对无载Q值的影响,考虑3个显著影响组件面,运用多因素影响分析方法可得到影响关系的权重模型如下:
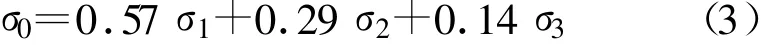
式中,σ0为腔体综合射频有效电导率,σ1为谐振器射频有效电导率,σ2为腔体底面射频有效电导率,σ3为腔体侧面射频有效电导率。该式表明,圆形同轴谐振腔3个表面射频有效电导率对无载Q值有显著影响,其影响权重比约为4∶2∶1。
谐振腔谐振回路阻值由接缝处集中接触阻抗及表面分布阻抗两部分组成,传统计算模型由于只引入了材料电导率来反映表面分布阻抗对无载Q值的影响而忽略了集中接触阻抗的影响。根据RLC串联回路衰减系数 α=R/2L可知,无载Q值与谐振回路阻值成反比关系,因此可在传统计算模型的基础上再次引入腔体接缝处集中接触阻抗及其影响系数。设同轴谐振腔各接缝处的集中接触阻抗为R0,表面分布阻抗为R′0,则其无载Q值为

式中,Q′u为谐振腔工程实际模型的无载Q值,Qu为腔体理想模型无载Q值,R0为集中接触阻抗,R′0为表面分布阻抗。当集中接触阻抗R0为0时则有Q′u=Qu。
由于同轴谐振腔谐振回路又不同于RLC串联回路,集中接触阻抗R0既不等于各接缝处集中接触阻抗Rn的平均值,也不等于这些阻抗值的和,即各处集中接触阻抗Rn对无载Q值的影响权重是不一致的。对于圆形同轴谐振腔装配连接质量对无载Q值的影响,根据上节分析结果,考虑两个显著影响因素,运用多因素影响分析方法可得到影响关系的权重模型如下:
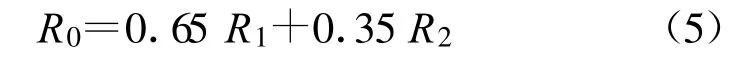
式中,R1为谐振器装配接缝处集中接触阻抗,R2为腔体底面装配接缝处集中接触阻抗。该式表明,圆形同轴谐振腔两个装配接缝对无载Q值有显著影响,其影响权重比约为2∶1。
综合式(1)、(3)、(4)、(5),对于圆形同轴谐振腔得到机械结构因素影响无载Q值的多因素分析计算公式为

该模型除保留了传统计算公式的基本要素外,加入了谐振腔组件表面射频有效电导率及装配连接质量对无载Q值的影响因素,同时对各组件机械结构因素进行了分解,建立了影响权重关系模型,应用于工程领域将明显提高计算的准确性。
4 结 论
本文综合运用了机械和微波工程理论,研究了同轴谐振腔不同组件表面、组件间接缝处机械结构因素对无载Q值的影响机理,在传统理想模型的基础上得到了机械结构因素影响无载Q值的层次化关系模型及工程计算公式。本文的研究工作紧密结合工程实践,得到的结论与大量工程经验和实测数据相吻合,对相关应用领域的优化设计、研究工作以及相关产品的加工工艺、装配调试工作有一定的指导作用。
[1]林为干.微波理论与技术[M].北京:科学出版社,1979.LIN Wei-gan.The Theory and Technology about Microwave[M].Beijing:China Science Press,1979.(in Chinese)
[2]黄志洵.截止波导理论[M].2版.北京:中国计量出版社,1989.HUANG Zhi-xun.The Theory of Waveguide below Cutoff[M].2nd ed.Beijing:China Metrology Publishing Company,1989.(in Chinese)
[3]柳光福,刘启明,葛光楣.介质谐振腔滤波器的设计[J].航空电子技术,2004,35(1):32-36,41.LIU Guang-fu,LIU Qi-ming,GEGuang-mei.Design of a Bandpass Filter Using Dielectric Ring Resonators[J].Avionics Technology,2004,35(1):32-36,41.(in Chinese)
[4]熊长武,胡国高,王勇.射频电导轮廓的概念及应用[J].电讯技术,2008,48(6):21-24.XIONG Chang-wu,HU Guo-gao,WANG Yong.The Concept and Application of RF Conductance Profile[J].Telecommunication Engineering,2008,48(6):21-24.(in Chinese)
[5]熊长武,王勇.微波器件表面射频等效电导率的分析计算[J].电子机械工程,2008(增):159-163.XIONG Chang-wu,WANG Yong.Analysis and Computation of Microwave Devices Surface RF Equivalent Conductivity[J].Telcotro-Mechanical Engineering,2008(Suppl.):159-163.(in Chinese)

